Preorder Tree Traversal without Recursion in C

March 1, 2023

Preorder Tree Traversal Implementation in C

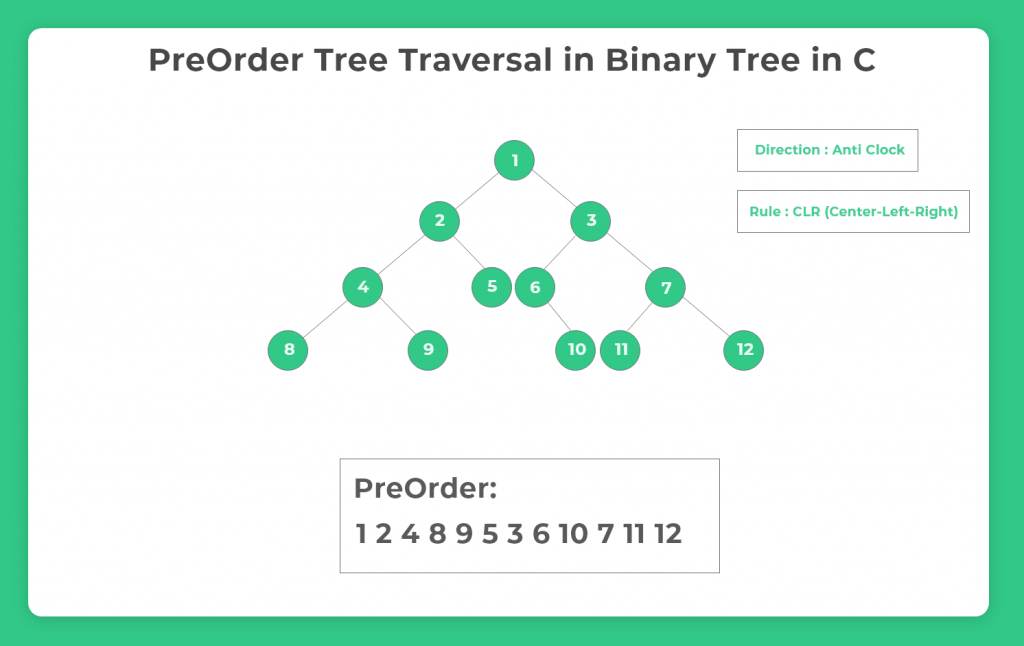
We can perform Preorder Tree Traversal without Recursion in C in two ways, First we can use stack and other one is iterative method known as morris traversal. In given example we are using stack method to perform Preorder traversal on tree. Preorder traversal of tree is Root->Left->Right. Here we will learn how to implement preorder traversal of tree using stack and its algorithm.

Steps for Implementing Preorder Tree traversal in C

In Following Steps we have define how to implement Preorder tree traversal without recursion in C :

Take an empty stack.
Push the root of the tree in stack.
Take the temporary node and initialize it with root node of tree.
Print the node and push the left node of temp node in stack and initialize temp from temp->left.
do the same task till left node temp is not null.
If temp become null and stack is not empty then pop the element from the stack and initialize temp from Poped element’s right node.
do the same task of pushing left node of and initializing temp from temp left.
If temp is null and stack is empty then return.

Algorithm for Preorder Traversing in Tree

Inorder_Traversal()

Flag = 1
WHILE(Flag)
IF(Temp)
PRINT(Temp->data)
push(Temp)
Temp = Temp->Left
END IF
ELSE
IF(isEmpty() == 0)
Temp = pop()
Temp = Temp->Right
ELSE
Flag =0
END ELSE
END ELSE

Priority Queue in C

Tree Traversals: Inorder Postorder Preorder

Inorder Tree Traversal in Binary Tree

Postorder Tree Traversal in Binary Tree

Postorder Tree Traversal without Recursion

C Program for Preorder Tree Traversing without Recursion

Run

#include<stdio.h>
#include<stdlib.h>
struct node			// node defining for tree
{
  struct node *left;
  struct node *right;
  int data;
};

struct stack			// node defining for stack
{
  struct node *data;
  struct stack *next;
};

void push (struct stack **top, struct node *n);	//function declation
struct node *pop (struct stack **top);
int isEmpty (struct stack *top);

int tree_traversal (struct node *root)	//Inorder Traversing function
{
  struct node *temp = root;
  struct stack *s_temp = NULL;
  int flag = 1;
  while (flag)			//Loop run untill temp is null and stack is empty
    {
      if (temp)
	{
	  printf ("%d ", temp->data);
	  push (&s_temp, temp);
	  temp = temp->left;
	}
      else
	{
	  if (!isEmpty (s_temp))
	    {
	      temp = pop (&s_temp);
	      temp = temp->right;
	    }
	  else
	    flag = 0;
	}
    }
}

void push (struct stack **top, struct node *n)	//push node in stack
{
  struct stack *new_n = (struct stack *) malloc (sizeof (struct stack));
  new_n->data = n;
  new_n->next = (*top);
  (*top) = new_n;
}

int isEmpty (struct stack *top)	// check if stack is empty
{
  if (top == NULL)
    return 1;
  else
    return 0;
}

struct node *pop (struct stack **top_n)	// pop the node from stack
{
  struct node *item;
  struct stack *top;
  top = *top_n;
  item = top->data;
  *top_n = top->next;
  free (top);
  return item;
}

struct node *create_node (int data)		// create a node for tree
{
  struct node *new_n = (struct node *) malloc (sizeof (struct node));
  new_n->data = data;
  new_n->left = NULL;
  new_n->right = NULL;
  return (new_n);
}

int main ()
{
  struct node *root;
  root = create_node (8);
  root->left = create_node (5);
  root->right = create_node (4);
  root->left->left = create_node (7);
  root->left->right = create_node (6);
  tree_traversal (root);
  return 0;
}

output:

8 5 7 6 4

Program Explanation:

Struct Node{} :

We are defining a structure node with integer data and two pointer pointers for left and right node.

Struct Stack{} :

Stack is the structure with a node data type data element and a pointer next.

Tree_traversal() :

In tree traversal function we Print the node and traverse the tree left node untill we found null when there is null we backtrack in tree with the help of stack and pop the element and print it.
Check if there is right child of that node if yes then again we traverse it left of the node.
We do the same task again and again till temp node is empty and stack is empty.

Push() :

Push function is use to push node from the tree into stack.

Pop() :

Pop function is use for remove the node from stack and return it.

IsEmpty() :

isEmpty checks if stack is empty or not if yes then it returns 1 and else it returns 0.

Create_node():

We are using create node function to create nodes for tree.

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Checkout list of all the video courses in PrepInsta Prime Subscription

Introduction to Trees

Binary Trees

Binary Tree in Data Structures (Introduction)
Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
Inorder Postorder PreOrder Traversals Examples
- Inorder Tree Traversal in Binary Tree: C | C++ | Java
- Preorder Tree Traversal in Binary Tree : C | C++ | Java
- Postorder Tree Traversal in Binary Tree : C | C++ | Java
Tree Traversal without Recursion
- Postorder Preorder Inorder Traversal without recursion
- Inorder Tree Traversal without Recursion – C | C++ | Java
- Preorder Tree Traversal without Recursion – C | C++ | Java
- Postorder Tree Traversal without Recursion – C | C++ | Java

Binary Search Trees

Binary search tree in Data Structures (Introduction)
- BST: Introduction to Binary Search Tree
- BST: Binary Search Tree Program : C | C++ | Java
- BST: Search a node in Binary Search Tree : C | C++ | Java
- BST: Insertion in a Binary Search Tree : C | C++ | Java
- BST: Deletion in a Binary Search Tree : C | C++ | Java

Traversals

Traversal in Trees
Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
Tree Traversals: Depth First Search (DFS) : C | C++ | Java
Construct a Binary Tree from Postorder and Inorder

B – Trees

B-Tree
- B-Tree: Introduction
- B-Tree: Insertion : C | C++ | Java
- B-Tree: Deletion : C | C++ | Java

AVL Trees

AVL Trees
- AVL Trees: Introduction
- AVL Tree Insertion : C | C++ | Java
- AVL Tree Deletion : C | C++ | Java
- Insertion in a Binary Tree (Level Order) – C | C++ | Java
- Searching in Binary Tree – C | C++ | Java
- Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

Depth First Traversals – C | C++ | Java
Level Order Traversal – C | C++ | Java
Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
Find size of the Binary tree – C | C++ | Java
Find the height of binary tree – C | C++ | Java
Find maximum in binary tree – C | C++ | Java
Check whether two tree are identical- C| C++| Java
Spiral Order traversal of Tree- C | C++| Java
Level Order Traversal Line by Line – C | C++| Java
Hand shaking lemma and some Impotant Tree Properties.
Check If binary tree if Foldable or not.- C| C++| Java
check whether tree is Symmetric – C| C++| Java.
Check for Children-Sum in Binary Tree- C|C++| Java
Sum of all nodes in Binary Tree- C | C++ | Java
Lowest Common Ancestor in Binary Tree- C | C++ | Java