Postorder Tree Traversal Without Recursion in C++
Postorder Tree Travesal Without Recursion
There are three types of traversals in trees: Preorder, Inorder and Postorder. The traversals can be performed using recursion or stack. In this article, postorder traversal is performed using two stacks. The Last In First Out principle of stack is used to get the postorder sequence. This approach helps avoid recursion and makes the traversal easier to manage in an iterative way.
It ensures nodes are processed in the correct left–right–root order without using function calls.
More About Postorder Traversal:
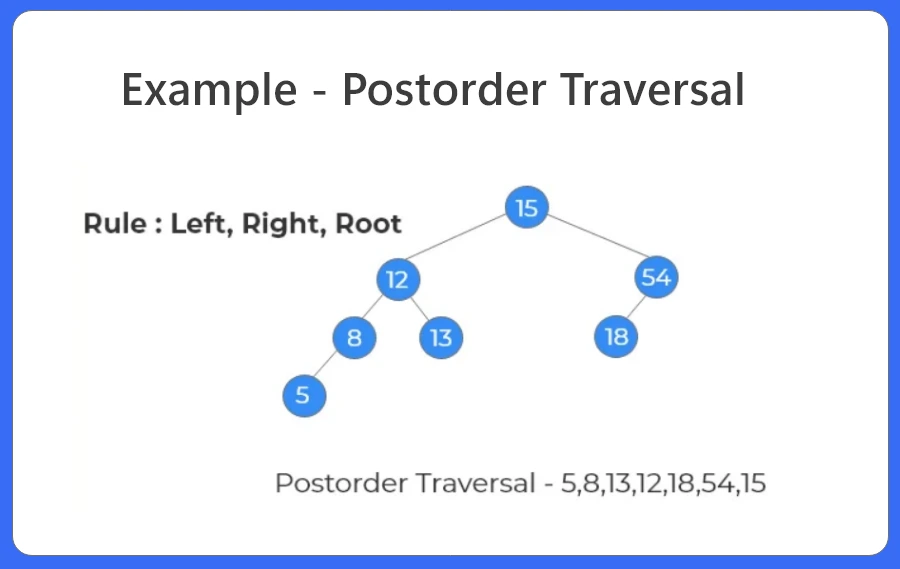
- Postorder traversal is a depth first algorithm.
- In postorder traversal, we first move to the left subtree then to the right subtree and finally print the node.
- Post order traversal is used when we want to free the nodes of the tree.
- It is also used to find the postfix expression.
Algorithm:
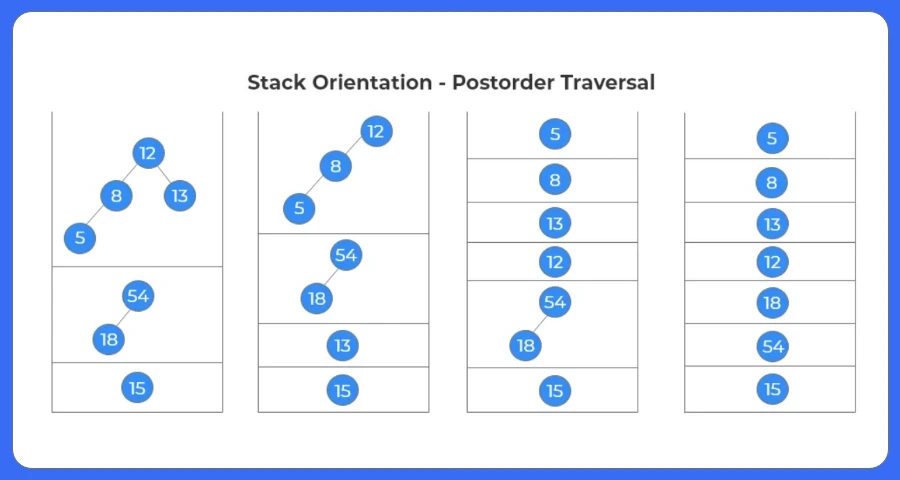
- Create two stacks: s1 and s2.
- Push the root in s1.
- Continue until s1 is empty.
- Pop the top element of s1 and push it into s2.
- Push the left and the right child of top element to s1.
- Print the s2 stack when s1 is empty.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Code Implementation for Postorder Tree traversal without recursion
Postorder tree traversal without recursion uses an iterative approach with the help of a stack to process nodes in the correct left–right–root sequence. This method avoids the overhead of recursive calls while still ensuring that each node is visited after its subtrees. It is efficient and commonly used when recursion is not preferred.
- It processes the left subtree first, then the right subtree, and finally the root node using stack-based logic.
#include<bits/stdc++.h>
using namespace std;
class Tree
{
public:
int data;
Tree *left = NULL, *right = NULL;
// Constructor initialised
Tree (int x)
{
data = x;
left = NULL;
right = NULL;
}
};
void postorder (Tree * root)
{
// If empty return;
if (root == NULL)
return;
stack < Tree * >s1, s2;
Tree *temp = root;
s1.push (temp);
// Continue till stack is empty
while (!s1.empty ())
{
temp = s1.top ();
s1.pop ();
// Push the top element of first stack
s2.push (temp);
// Push the left child of the top element
if (temp->left != NULL)
s1.push (temp->left);
// Push the right child of the top element
if (temp->right != NULL)
s1.push (temp->right);
}
// Print the second stack
while (!s2.empty ())
{
cout << s2.top ()->data << " ";
s2.pop ();
}
cout << endl; } int main () { Tree *root = new Tree (10); root->left = new Tree (20);
root->right = new Tree (30);
root->left->left = new Tree (40);
root->left->right = new Tree (50);
cout << "Postorder Traversal" << endl;
postorder (root);
return 0;
}
Output:
Postorder Traversal 40 50 20 30 10
Explanation:
- The code uses two stacks (s1 and s2) to perform postorder traversal without recursion, simulating the natural left–right–root behavior of the recursive method.
- The first stack pushes nodes in a way that ensures the second stack receives them in reverse postorder order, helping to print the correct postorder sequence later.
- Each node is popped from s1, pushed into s2, and then its left and right children are pushed into s1 if they exist, ensuring all nodes are processed.
- After the first loop completes, the second stack contains the nodes in proper postorder order, so popping and printing from s2 gives the correct traversal output.
- The main() function creates a sample binary tree and calls the postorder traversal function, which prints elements in the correct postorder sequence.
Time and Space Complexity:
| Operation | Time Complexity | Space Complexity |
|---|---|---|
| Postorder Traversal (Using Two Stacks) | O(n) | O(n) |
To Wrap It Up:
The postorder traversal without recursion offers a reliable way to visit nodes in Left–Right–Root order by using stacks instead of recursive calls. This approach helps avoid function call overhead and maintains full control over the flow of traversal.
By using an iterative method, the tree is processed efficiently, making it suitable for large structures where recursion might lead to stack overflow or unnecessary complexity.
FAQs
It is an iterative method to visit nodes in Left–Right–Root order using stacks instead of recursive function calls. This ensures depth-first traversal without using system recursion.
Two stacks help maintain the correct postorder sequence by first collecting nodes and then reversing their order. This guarantees that the final output follows the Left–Right–Root pattern.
It’s commonly used when child nodes must be processed before the parent, such as deleting a tree or evaluating expression trees. This makes it valuable in memory management and compiler design.
The iterative approach is safer for large trees because it avoids stack overflow and provides better control. It also removes dependency on function call recursion, making it more stable in deep trees.
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others




Login/Signup to comment