Post-order tree traversal in C

March 1, 2023

Post-order tree traversal without recursion

 

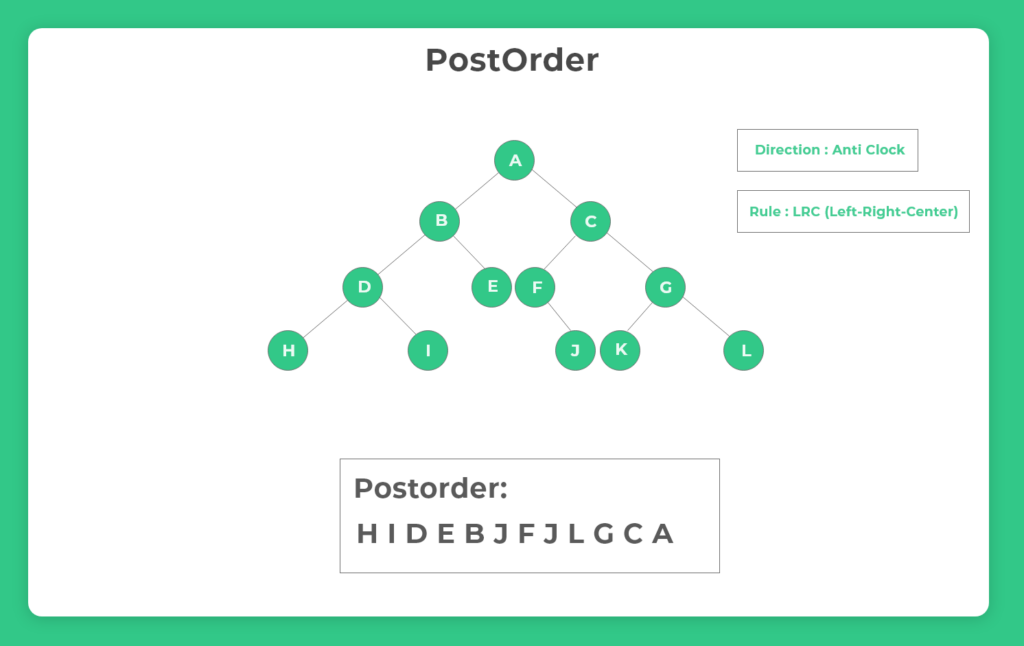
In postorder traversal , first we traverse the left subtree, then the right subtree and finally the root node. Postorder traversal is also used to get the postfix expression of an expression given.In this post , post-order tree traversal without recursion is discussed using one stacks.

TCS Coding Questions 2022 Day 4 Slot 1

Postorder Tree Traversal without recursion in C

Algorithm :

  • Create an empty stack.
  • While root is not NULL, push root->right and then root to the stack.
  • And Set root as root->left.
  • If root becomes NULL, pop item from the stack and set it as root.
  • If the popped item has a right child and the right child is at top of stack, then remove the right child from stack, push the root back and set root as root’s right child.
  • Else print root’s data and set root as NULL.
  • Repeat the above two steps until stack is not empty.
Postorder Tree Traversal in Binary Tree in C
DSA desktop gif
DSA mobile gif

Priority Queue in C

Tree Traversals: Inorder Postorder Preorder

Inorder Tree Traversal in Binary Tree

Inorder Tree Traversal without Recursion

Preorder Tree Traversal without Recursion

Code based on above algorithm :

Run 
#include<stdio.h>
#include<stdlib.h>
#define MAX_SIZE 100
struct Node
{
  int data;
  struct Node *left, *right;
};

struct Stack
{
  int size;
  int top;
  struct Node **array;
};

struct Node *newNode (int data)
{
  struct Node *node = (struct Node *) malloc (sizeof (struct Node));
  node->data = data;
  node->left = node->right = NULL;
  return node;
}

struct Stack *createStack (int size)
{
  struct Stack *stack = (struct Stack *) malloc (sizeof (struct Stack));
  stack->size = size;
  stack->top = -1;
  stack->array =
    (struct Node **) malloc (stack->size * sizeof (struct Node *));
  return stack;
}

int isFull (struct Stack *stack)
{
  return stack->top - 1 == stack->size;
}

int isEmpty (struct Stack *stack)
{
  return stack->top == -1;
}

void push (struct Stack *stack, struct Node *node)
{
  if (isFull (stack))
    return;
  stack->array[++stack->top] = node;
}

struct Node *pop (struct Stack *stack)
{
  if (isEmpty (stack))
    return NULL;
  return stack->array[stack->top--];
}

struct Node *peek (struct Stack *stack)
{
  if (isEmpty (stack))
    return NULL;
  return stack->array[stack->top];
}

void postorder (struct Node *root)
{
  if (root == NULL)
    return;

  struct Stack *stack = createStack (MAX_SIZE);
  do
    {
      while (root)
	{
	  if (root->right)
	    push (stack, root->right);
	  push (stack, root);

	  root = root->left;
	}

      root = pop (stack);

      if (root->right && peek (stack) == root->right)
	{
	  pop (stack);
	  push (stack, root);
	  root = root->right;

	}
      else
	{
	  printf ("%d ", root->data);
	  root = NULL;
	}
    }
  while (!isEmpty (stack));
}

int main ()
{

  struct Node *root = NULL;
  root = newNode (10);
  root->left = newNode (20);
  root->right = newNode (30);
  root->left->left = newNode (40);
  root->left->right = newNode (50);
  root->right->left = newNode (60);
  root->right->right = newNode (70);
  printf ("Post order traversal of binary tree is :\n");
  printf ("[");
  postorder(root);
  printf ("]");

  return 0;
}

Output :

Post order traversal of binary tree is :
[40 50 20 60 70 30 10]

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion : C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal Line by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric – C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree- C | C++ | Java

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion :  C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal LIne by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric  C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree. C | C++ | Java

One comment on “Post-order tree traversal in C”


  • akanksha

    Why can’t we use same stack structure in post order traversal as we used in per order traversal
    Per order traversal
    struct snode
    {
    struct snode *s
    struct tnode * t;
    }

    Post order traversal
    struct stack
    {
    int top;
    int size;
    struct node ** array;
    };