Insertion in a Binary Tree (Level Order) in Java

March 22, 2023

Insertion in Binary Tree

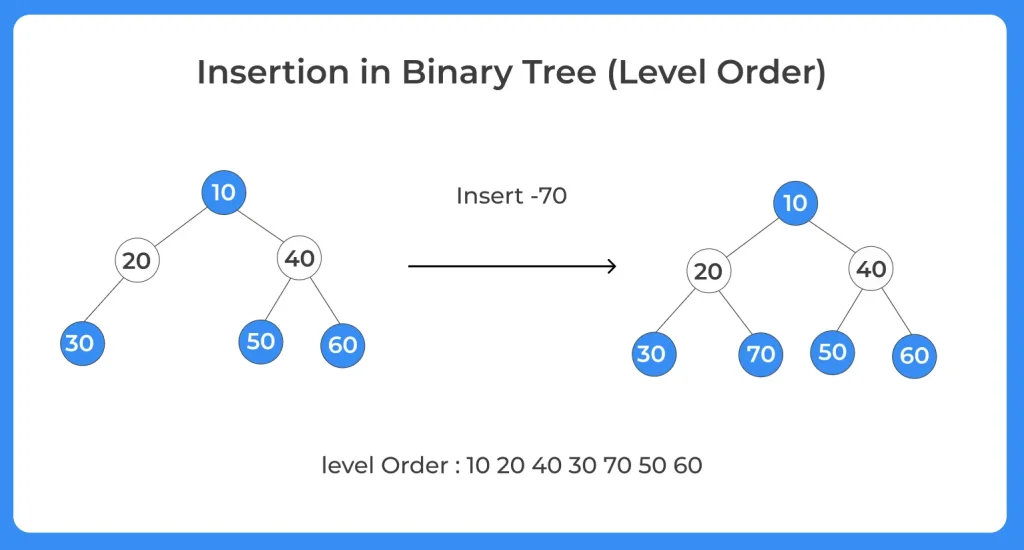
Insertion in Binary Tree is being discussed in this article. A binary tree can be defined as a finite set of elements, which can either be empty or have at most two children. Given a tree and a key, add a node in the first available node in the tree. After adding the node, print the level order traversal. 

insertion in binary tree

Binary Tree

  • A Binary Tree is a data structure with maximum of two children for each parent.
  • Level Order Traversal is an example Of Breadth First Search algorithm.
  • Level order is a traversal in which each node is visited in the level before we move to a lower level.
  • Queues are used to find the level order traversal.
Insertion in Binary Tree (Level Order)
DSA desktop gif
DSA mobile gif

Searching in a Binary Search Tree

AVL Tree Insertion

Depth First Traversals

Level Order Traversal

Construct Tree from given Inorder and Preorder traversals

Algorithm

  • Iterate level order traversal of the given tree using queue.
  • If we find a node whose left child is empty, we make new key as left child of the node.
  • Else if we find a node whose right child is empty, we make the new key as right child. 
  • Keep traversing the tree until we find a node whose wither left or right child is empty.
Run 
import java.util.*;
class Node
{
  int value;
  Node left, right;


    Node (int value)
  {
    this.value = value;
    left = right = null;
  }
}

class Main
{
  static Node root;
  //static Node temp=root;
  public static void inorder (Node ptr)
  {
    if (ptr == null)
      return;
    inorder (ptr.left);

    System.out.print (ptr.value + " ");
    inorder (ptr.right);
  }

  public static void insert (Node ptr, int item)
  {
    if (ptr == null)
      {
	root = new Node (item);
	return;
      }
    Queue < Node > que = new LinkedList < Node > ();
    que.add (ptr);

    while (!que.isEmpty ())
      {
	ptr = que.peek ();
	que.remove ();
	if (ptr.left == null)
	  {
	    ptr.left = new Node (item);
	    break;
	  }
	else
	  que.add (ptr.left);

	if (ptr.right == null)
	  {
	    ptr.right = new Node (item);
	    break;
	  }
	else
	  que.add (ptr.right);
      }
  }


  public static void main (String[]args)
  {
    Node root = new Node (10);
    root.left = new Node (20);
    root.left.left = new Node (30);
    root.right = new Node (40);
    root.right.left = new Node (50);
    root.right.right = new Node (60);

    System.out.println ("Inorder Traversal before Insertion: ");
    inorder (root);

    int item = 7;
    insert (root, item);

    System.out.println ("\nInorder Traversal after insertion");

    inorder (root);
  }
}

Output:

Inorder Traversal before Insertion: 
30 20 10 50 40 60 
Inorder Traversal after insertion
30 20 70 10 50 40 60

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion :  C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal LIne by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric  C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree. C | C++ | Java

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion : C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal Line by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric – C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree- C | C++ | Java