Inorder Tree Traversal Without Recursion In C++

August 8, 2025

Inorder Tree Traversal Without Recursion

Inorder Tree Traversal Without Recursion In C++ – Inorder traversal means visiting the left part of the tree first, then the root, and finally the right part. It’s a common way to go through all the nodes of a binary tree. Usually, we do this using recursion, but sometimes using recursion can cause issues if the tree is too big. So instead, we can do it without recursion by using a stack. In this method, we manually manage the steps that recursion would handle.

There are three types of traversals in trees: Preorder, Inorder and Postorder. The traversals can be performed using recursion or stack. In this article, inorder traversal is performed using stacks.

More About Inorder Traversal

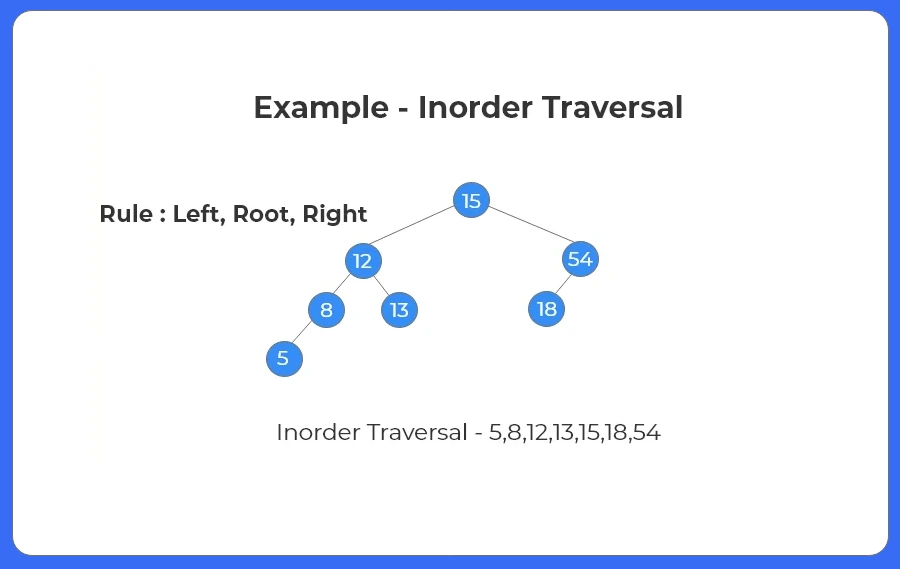
Inorder Traversal is a depth first algorithm.
In Inorder Traversal, we first move to the left subtree, then print the node and finally move to the right subtree.
If you want the orginal sequence or how the tree was made, we use the inorder sequence.
Inorder Traversal of a binary search tree gives the sequence in non decreasing order.

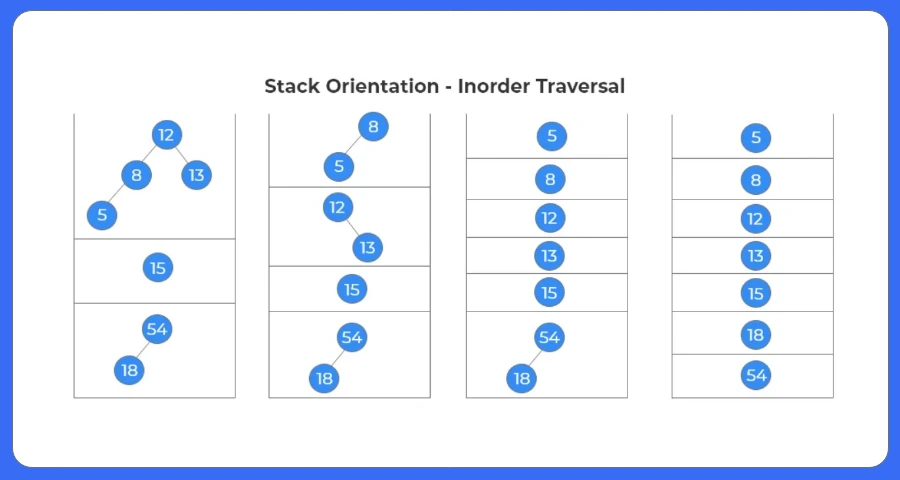
Algorithm for Inorder Tree Traversal Without Recursion In C++:

Return if root is empty.
Store temp as root.
Continue the while loop until temp is not null or stack is not empty.
Keep adding the left child of temp until NULL is encountered.
Print the temp node.
Since all the left children are visited, change temp to its right child.

What is Inorder generally used for?

We generally use Inorder traversal technique on Binary Tress , as it fetches the values from the underlying set in order. Using Post-order traversal is also an option, but during post order traversal while delete or freeing nodes it can even delete or free an entire binary tree, which is not a favorable condition.

Inorder Postorder Preorder Traversal Examples

Preorder Tree Traversal in Binary Tree

Postorder Tree Traversal in Binary Tree

Preorder Tree Traversal without Recursion

Postorder Tree Traversal without Recursion

Algorithm To Find Inorder Traversal:

If root is NULL, return NULL.
Visit the left subtree.
Print the node.
Visit the right subtree.

Code Implementation for Inorder Tree traversal

Run

#include<bits/stdc++.h>
using namespace std;

struct Node
{
	int data;
	struct Node* left;
	struct Node* right;
	Node (int data)
	{
		this->data = data;
		left = right = NULL;
	}
};

void inOrder(struct Node *root)
{
	stack s;
	Node *curr = root;

	while (curr != NULL || s.empty() == false)
	{
		while (curr != NULL)
		{
			s.push(curr);
			curr = curr->left;
		}

		curr = s.top();
		s.pop();

		cout << curr->data << " ";
		curr = curr->right;

	} 
}

int main()
{

	struct Node *root = new Node(1);
	root->left	 = new Node(2);
	root->right	 = new Node(3);
	root->left->left = new Node(4);
	root->left->right = new Node(5);

	inOrder(root);
	return 0;
}

Output:
4 2 5 1 3

Conclusion – Inorder Tree Traversal Without Recursion in C++

Inorder traversal without using recursion is a smart way to go through a binary tree when you want to avoid the limitations of recursive calls. By using a stack, we can keep track of nodes ourselves and visit them in the correct Left–Root–Right order. It might seem tricky at first, but once you understand how the stack helps in the process, it becomes much easier.

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

FAQs - Inorder Tree Traversal Without Recursion in C++

How does the iterative method maintain the same order as recursive inorder traversal?

In the recursive method, the system stack automatically tracks function calls for the left and right subtrees. In the iterative method, we manually use a stack to mimic this behavior. We first go deep into the leftmost node, pushing nodes onto the stack. Once we reach the end, we process the top node (root), then move to its right child—just like the recursive Left–Root–Right order.

What are the edge cases to handle in iterative inorder traversal?

Some common edge cases include:

The tree is completely empty (root == NULL)
The tree has only one node (no left or right child)
The tree is skewed (all left or all right nodes)
You should make sure the code works for all these cases and does not throw null pointer or segmentation errors.

What is the time and space complexity of the non-recursive inorder traversal using stack?

Time Complexity: O(n), where n is the number of nodes. Every node is visited once.
Space Complexity: O(h), where h is the height of the tree. The stack stores at most h nodes at a time in the worst case.

Can we perform inorder traversal without using both recursion and stack?

Yes, this can be done using Morris Traversal, which uses the concept of threaded binary trees. It avoids both stack and recursion by temporarily modifying the tree structure during traversal. However, it’s more complex and requires restoring the tree afterward.

How can we modify the iterative inorder traversal to store the result in a vector instead of printing it?

Instead of printing each node’s value, you can store it in a vector:

vector<int> result;
result.push_back(curr->data);

This is useful when you need to return the traversal result from a function or compare it with another tree.

Why might the iterative approach be preferred over recursion in production-level applications?

In large trees, recursion may cause stack overflow due to deep recursive calls. Iterative traversal avoids this risk by using heap memory for the stack. It also gives more control over the flow, better error handling, and is generally safer and more efficient in memory-constrained environments.

Introduction to Trees

Binary Trees

Binary Tree in Data Structures (Introduction)
Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
Inorder Postorder PreOrder Traversals Examples
- Inorder Tree Traversal in Binary Tree: C | C++ | Java
- Preorder Tree Traversal in Binary Tree : C | C++ | Java
- Postorder Tree Traversal in Binary Tree : C | C++ | Java
Tree Traversal without Recursion
- Postorder Preorder Inorder Traversal without recursion
- Inorder Tree Traversal without Recursion – C | C++ | Java
- Preorder Tree Traversal without Recursion – C | C++ | Java
- Postorder Tree Traversal without Recursion – C | C++ | Java

Binary Search Trees

Binary search tree in Data Structures (Introduction)
- BST: Introduction to Binary Search Tree
- BST: Binary Search Tree Program : C | C++ | Java
- BST: Search a node in Binary Search Tree : C | C++ | Java
- BST: Insertion in a Binary Search Tree : C | C++ | Java
- BST: Deletion in a Binary Search Tree : C | C++ | Java

Traversals

Traversal in Trees
Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
Tree Traversals: Depth First Search (DFS) : C | C++ | Java
Construct a Binary Tree from Postorder and Inorder

B – Trees

B-Tree
- B-Tree: Introduction
- B-Tree: Insertion : C | C++ | Java
- B-Tree: Deletion : C | C++ | Java

AVL Trees

AVL Trees
- AVL Trees: Introduction
- AVL Tree Insertion : C | C++ | Java
- AVL Tree Deletion : C | C++ | Java
- Insertion in a Binary Tree (Level Order) – C | C++ | Java
- Searching in Binary Tree – C | C++ | Java
- Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

Depth First Traversals – C | C++ | Java
Level Order Traversal – C | C++ | Java
Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
Find size of the Binary tree – C | C++ | Java
Find the height of binary tree – C | C++ | Java
Find maximum in binary tree – C | C++ | Java
Check whether two tree are identical- C| C++| Java
Spiral Order traversal of Tree- C | C++| Java
Level Order Traversal Line by Line – C | C++| Java
Hand shaking lemma and some Impotant Tree Properties.
Check If binary tree if Foldable or not.- C| C++| Java
check whether tree is Symmetric – C| C++| Java.
Check for Children-Sum in Binary Tree- C|C++| Java
Sum of all nodes in Binary Tree- C | C++ | Java
Lowest Common Ancestor in Binary Tree- C | C++ | Java