Construct Tree from given Postorder and Inorder Traversals in C++
Construct Tree From Given Inorder and Postorder traversals in C++
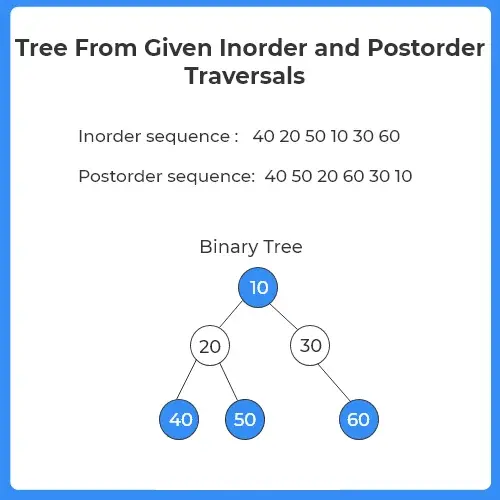
There are three types of traversals in a tree: Inorder, Preorder and Postorder traversal. A tree can be formed with any two tree traversals in which one of them being the in order traversal. In this article, we will learn about how to construct tree from given postorder and inorder traversals in C++.
Algorithm For InOrder Traversal:
- Traverse The Left subtree.
- Print the node.
- Traverse the right subtree.
Algorithm For PostOrder Traversal:
- Traverse the left subtree.
- Traverse the right subtree.
- Print the node.
Code Implementation for constructing tree from postorder and inorder traversals in C++
Run
#include<bits/stdc++.h>
using namespace std;
class Tree
{
public:
int data;
Tree *left = NULL, *right = NULL;
Tree (int x)
{
data = x;
left = NULL;
right = NULL;
}
};
int search (int inorder[], int start, int end, int element)
{
int i = 0;
for (i = start; i < end; i++)
{
if (inorder[i] == element)
return i;
}
return i;
}
void printInorder (Tree * node)
{
if (node == NULL)
return;
printInorder (node->left);
cout << node->data << " ";
printInorder (node->right);
}
Tree *build_tree (int inorder[], int postorder[], int start, int end)
{
static int index = end + 1;
if (start > end)
return NULL;
Tree *curr_node = new Tree (postorder[index--]);
int x = curr_node->data;
if (start == end)
return curr_node;
int search_index = search (inorder, start, end, x);
curr_node->right = build_tree (inorder, postorder, search_index + 1, end);
curr_node->left = build_tree (inorder, postorder, start, search_index - 1);
return curr_node;
}
int main ()
{
int in[] = { 12, 25, 30, 37, 40, 50, 60, 62, 70, 75, 87 };
int post[] = { 12, 30, 40, 37, 25, 60, 70, 62, 87, 75, 50 };
Tree *root = build_tree (in, post, 0, 10);
cout << "Inorder traversal\n";
printInorder (root);
return 0;
}
Output: Inorder traversal 12 25 30 37 40 50 60 62 70 75 87
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java
Login/Signup to comment