Boyer–Moore majority vote algorithm in C

June 27, 2025

Boyer-Moore majority vote algorithm

Boyer–Moore majority vote algorithm in C is one of the popular optimal algorithms which is used to find the majority element among the given elements of the array, that have more than N/ 2 occurrences. Boyer–Moore’s majority vote algorithm works perfectly fine for finding the majority element which takes 2 traversals over the given elements, which works in O(N) time complexity and O(1) space complexity.

Boyer-Moore Majority Vote Algorithm in C_

Boyer-Moore Majority Vote Algorithm in C

The Boyer-Moore Majority Vote Algorithm is an efficient algorithm for finding the majority element in an array, which is an element that appears more than n/2 times, where n is the length of the array.

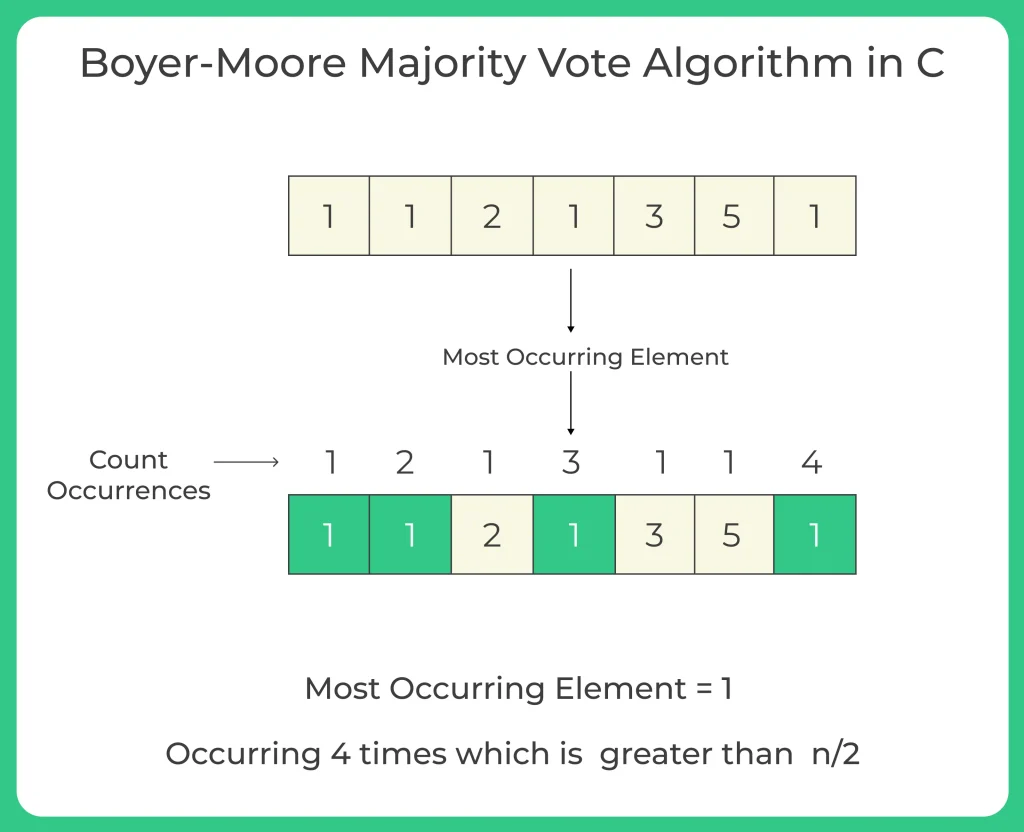
Boyer-Moore Majority Vote Algorithm in C

Example:

Input: k = 6,  arr = [ 1, 2, 5, 2, 2, 2 ]

Output: Majority Element is 2
DSA desktop gif
DSA mobile gif

Size of sub-array with max sum

Sub-array with given sum

Triplet that sum to a given value

Segregate 0’s and 1’s in array 

Sort elements in array by frequency

Algorithm for Boyer-Moore Majority Vote Algorithm in C:

  • Take the size of the array and store it in variable n.
  • Take n elements of the array from the user.
  • Declare two variables one is maj_index and initialize it with 0, and one variable count with value 0.
  • Run a loop from index 1 to n-1
  • Check if a[i]==a[maj_index] then increase the value of count by 1, else decrease it by 1.
  • If count becomes zero then set maj_index=i and count =1.
  • Now create one function check that will check whether the maj_index value presents n/2 times or not.
  • If it is present then return 1, otherwise 0(means no elements present more than n/2 times).

C code

Run

#include<stdio.h>

int find_majority (int a[], int size)
{
  int maj_index = 0, count = 1;

  for (int i = 1; i < size; i++)
    {
      if (a[i] == a[maj_index])
	count++;
      else
	count--;

      if (count == 0)
	{
	  maj_index = i;
	  count = 1;
	}
    }
  return a[maj_index];
}

int check_maj (int a[], int n, int k)
{
  int count = 0;

  for (int i = 0; i < n; i++) { if (a[i] == k) count++; } if (count > n / 2)
    return 1;
  else
    return 0;
}

int main ()
{
  int k;
  int a[] = { 3, 3, 4, 2, 4, 4, 2, 4, 4 };
  int n = sizeof (a) / sizeof (a[0]);
  k = find_majority (a, n);

  if (check_maj (a, n, k))
    printf ("Majority element is %d", k);
  else
    printf ("No Majority element\n");

  return 0;
}

Output:

 Majority Element is 4

Conclusion - Boyer-Moore Majority Vote Algorithm in C

The Boyer–Moore Majority Vote Algorithm is a smart and efficient way to find the majority element in an array — the one that appears more than half the time. It works in O(n) time and uses only O(1) space, making it very useful when dealing with large arrays.

The algorithm has two steps: first, it finds a potential candidate for the majority element by increasing or decreasing a count while looping through the array. Then, it checks if the candidate actually appears more than n/2 times.

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

FAQs - Frequently Asked Questions

The algorithm only identifies a potential majority element based on frequency balancing. It doesn’t guarantee that the candidate actually appears more than n/2 times. Hence, a second pass is essential to validate the count of the candidate and confirm its majority status.

Not directly. To find elements occurring more than n/3 times, the algorithm needs to track two candidates instead of one. This extended version is more complex and involves additional logic to manage and verify both candidates, but still maintains O(n) time and O(1) space.

The algorithm pairs different elements against each other, reducing the count when they differ. This works on the principle that the majority element will remain unmatched more often than others, thus surviving the cancellation and emerging as the final candidate.

In streaming data, the input is continuous and unbounded, and the majority element may shift. Boyer–Moore assumes a static dataset, so its count logic may become inaccurate if applied incrementally without adaptation to dynamic inputs.

If no element appears more than n/2 times, the algorithm will still return a candidate. However, that candidate will fail in the second pass verification, which is why that step is crucial. Without verification, the result would be incorrect.

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion : C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal Line by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric – C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree- C | C++ | Java

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion :  C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal LIne by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric  C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree. C | C++ | Java