Binary Search Tree: Deletion

March 2, 2023

Deletion In Binary Search Tree

A Binary Search Tree is a rooted binary tree whose internal nodes each a key greater than all the keys in the node’s left subtree and less than those in it’s right subtree. Delete function is used to delete the specified node from binary search tree. In this article we will perform deletion in binary search tree.

Deletion in a Binary Search Tree In C

Deletion in a Binary Search Tree has three possible ways of removal or elimination of a node.
It is important to keep in mind the property that serves as the foundation of a BST structure.
A tree is said to be a BST only if,

node(left_subtree) < root node < node(right_subtree).

Even when deleting a node from a BST, we should not disturb this important aspect of it.
Let us see the three possible ways in which a node can be deleted from a binary search tree.

The three possible cases in which we are supposed to delete any element from a binary search tree are:

The node to be deleted has no child nodes.
The node to be deleted has one child.
The node to be deleted has two child nodes.

Using the example we will study each case indivisually in detail.

Case 1: Deleting a node with no children :-

If the node to be deleted from the tree has no child nodes, the node is simple deleted from the tree since it is a leaf node.

Case 2: Deleting a node with two children :-

we first find the inorder predecessor of the node and replace the target node with the inorder predecessor.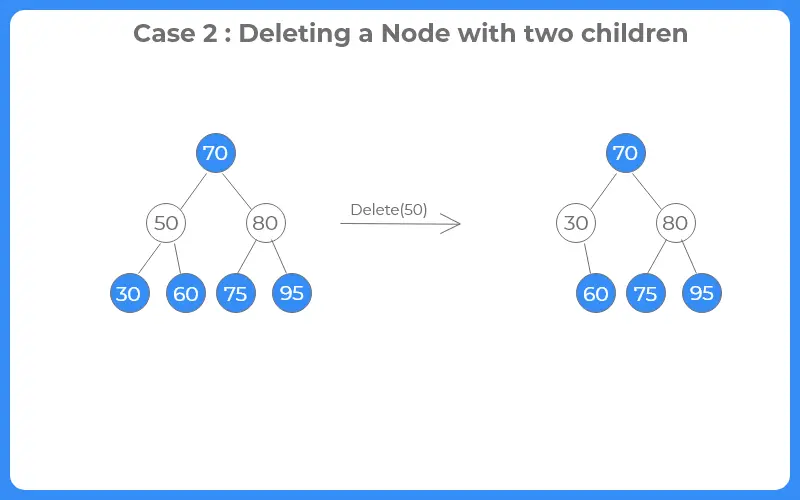

Case 3: Deleting a node with one child :-

If the node to be deleted has a single child node, the target node is replaced from its child node and then the target node is simply deleted.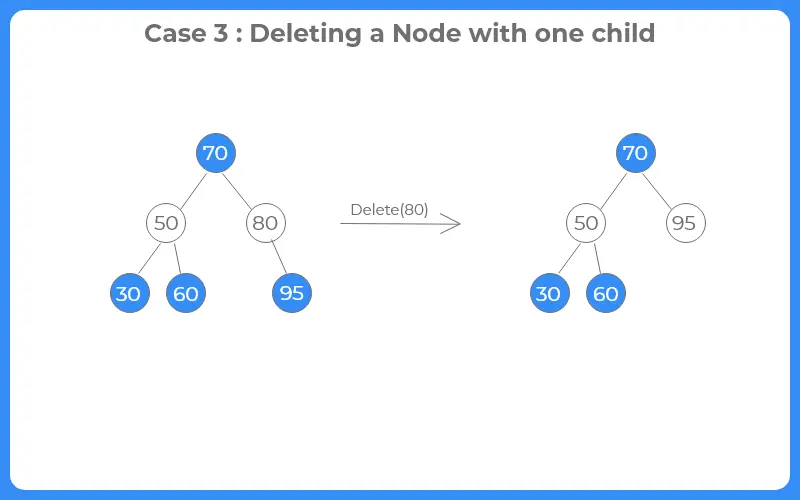

Tree Traversals: Inorder Postorder Preorder

BST: Binary Search Tree Program

BST: Search a node in Binary Search Tree

BST: Insertion in a Binary Search Tree

Tree Traversals: Depth First Search (DFS)

Implementation of Deletion In BST

Run

#include <stdio.h>
#include <stdlib.h>

struct node
{
  int data;
  struct node *left, *right;
};

struct node *newNode (int value)
{
  struct node *temp = (struct node *) malloc (sizeof (struct node));
  temp->data = value;
  temp->left = temp->right = NULL;
  return temp;
}

void inorderTraversal (struct node *root)
{
  if (root != NULL)
    {
      inorderTraversal (root->left);
      printf ("%d ", root->data);
      inorderTraversal (root->right);
    }
}

struct node *deleteNode (struct node *root, int key)
{
  if (root == NULL)
    return root;

  if (key < root->data)
    {
      root->left = deleteNode (root->left, key);
    }
  else if (key > root->data)
    {
      root->right = deleteNode (root->right, key);
    }
  else
    {
      if (root->left == NULL)
	{
	  struct node *temp = root->right;
	  free (root);
	  return temp;
	}
      else if (root->right == NULL)
	{
	  struct node *temp = root->left;
	  free (root);
	  return temp;
	}
      struct node *temp = root->right;
      while (temp->left != NULL)
	{
	  temp = temp->left;
	}
      root->data = temp->data;
      root->right = deleteNode (root->right, temp->data);
    }
  return root;
}

int main ()
{
  struct node *root = newNode (50);
  root->left = newNode (30);
  root->right = newNode (70);
  root->left->left = newNode (20);
  root->left->right = newNode (40);
  root->right->left = newNode (60);
  root->right->right = newNode (80);
  printf ("Inorder traversal of the original tree: ");
  inorderTraversal (root);

  int key = 50;
  root = deleteNode (root, key);
  printf ("\nInorder traversal after deleting %d: ", key);
  inorderTraversal (root);

  return 0;
}

Output:

Inorder traversal of the original tree: 20 30 40 50 60 70 80 
Inorder traversal after deleting 50: 20 30 40 60 70 80

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Checkout list of all the video courses in PrepInsta Prime Subscription

Introduction to Trees

Binary Trees

Binary Tree in Data Structures (Introduction)
Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
Inorder Postorder PreOrder Traversals Examples
- Inorder Tree Traversal in Binary Tree: C | C++ | Java
- Preorder Tree Traversal in Binary Tree : C | C++ | Java
- Postorder Tree Traversal in Binary Tree : C | C++ | Java
Tree Traversal without Recursion
- Postorder Preorder Inorder Traversal without recursion
- Inorder Tree Traversal without Recursion – C | C++ | Java
- Preorder Tree Traversal without Recursion – C | C++ | Java
- Postorder Tree Traversal without Recursion – C | C++ | Java

Binary Search Trees

Binary search tree in Data Structures (Introduction)
- BST: Introduction to Binary Search Tree
- BST: Binary Search Tree Program : C | C++ | Java
- BST: Search a node in Binary Search Tree : C | C++ | Java
- BST: Insertion in a Binary Search Tree : C | C++ | Java
- BST: Deletion in a Binary Search Tree : C | C++ | Java

Traversals

Traversal in Trees
Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
Tree Traversals: Depth First Search (DFS) : C | C++ | Java
Construct a Binary Tree from Postorder and Inorder

B – Trees

B-Tree
- B-Tree: Introduction
- B-Tree: Insertion : C | C++ | Java
- B-Tree: Deletion : C | C++ | Java

AVL Trees

AVL Trees
- AVL Trees: Introduction
- AVL Tree Insertion : C | C++ | Java
- AVL Tree Deletion : C | C++ | Java
- Insertion in a Binary Tree (Level Order) – C | C++ | Java
- Searching in Binary Tree – C | C++ | Java
- Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

Depth First Traversals – C | C++ | Java
Level Order Traversal – C | C++ | Java
Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
Find size of the Binary tree – C | C++ | Java
Find the height of binary tree – C | C++ | Java
Find maximum in binary tree – C | C++ | Java
Check whether two tree are identical- C| C++| Java
Spiral Order traversal of Tree- C | C++| Java
Level Order Traversal Line by Line – C | C++| Java
Hand shaking lemma and some Impotant Tree Properties.
Check If binary tree if Foldable or not.- C| C++| Java
check whether tree is Symmetric – C| C++| Java.
Check for Children-Sum in Binary Tree- C|C++| Java
Sum of all nodes in Binary Tree- C | C++ | Java
Lowest Common Ancestor in Binary Tree- C | C++ | Java