Sort Array in Waveform in C++
Sort Array in Waveform in C++ Language
This page is all about Sort Array in Waveform in C++ Language . To convert an array in waveform we can use two concepts.First method is Brute Force Solution — Using Sorting and second method is Incrementing the loop by two.
we will be learning about both of them in this page, their working and C++ program.

Sort Array in Waveform in C++ Language
Sorting an array in waveform refers to the process of rearranging the elements of the array in a specific manner, such that the resulting array represents a waveform-like pattern. In waveform sorting, the elements of the array are arranged in a way that alternates between ascending and descending order, mimicking the shape of a waveform with peaks and troughs.
For example, consider the following waveform sorted array:
[10, 5, 6, 2, 20, 3, 48, 30]
In this array, the first element 10 is the peak, the second element 5 is the valley, the third element 6 is the peak again, the fourth element 2 is the valley, the fifth element 20 is the peak and so on.

Method 1 : Brute Force Solution (using sorting)
The brute force solution using sorting involves the following steps:
Step 1: Sort the array in ascending order. For example, if the input array is {20, 30, 5, 25, 10, 15}, after sorting, we get {5, 10, 15, 20, 25, 30}.
Step 2: Swap all adjacent elements of the array. Using the sorted array from step 1, we swap adjacent elements to obtain the final result. For example, swapping adjacent elements in the sorted array {5, 10, 15, 20, 25, 30} would give us {10, 5, 20, 15, 30, 25}.
This method is simple but may not be the most efficient solution for larger arrays, as sorting has a time complexity of O(n log n) and swapping adjacent elements has a time complexity of O(n), resulting in an overall time complexity of O(n log n) + O(n), which can be further optimized.
If we plot step 1 (that is sorted array) on graph then it would look something like this.
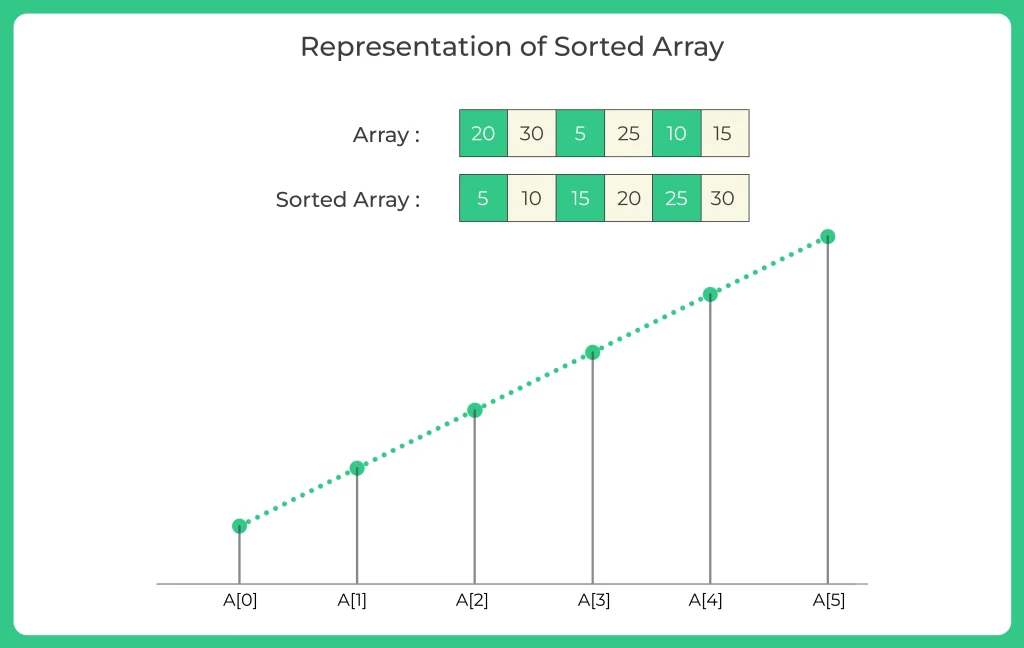
If we plot step 2 (that is swapping adjacent elements) on graph then it would look something like this.
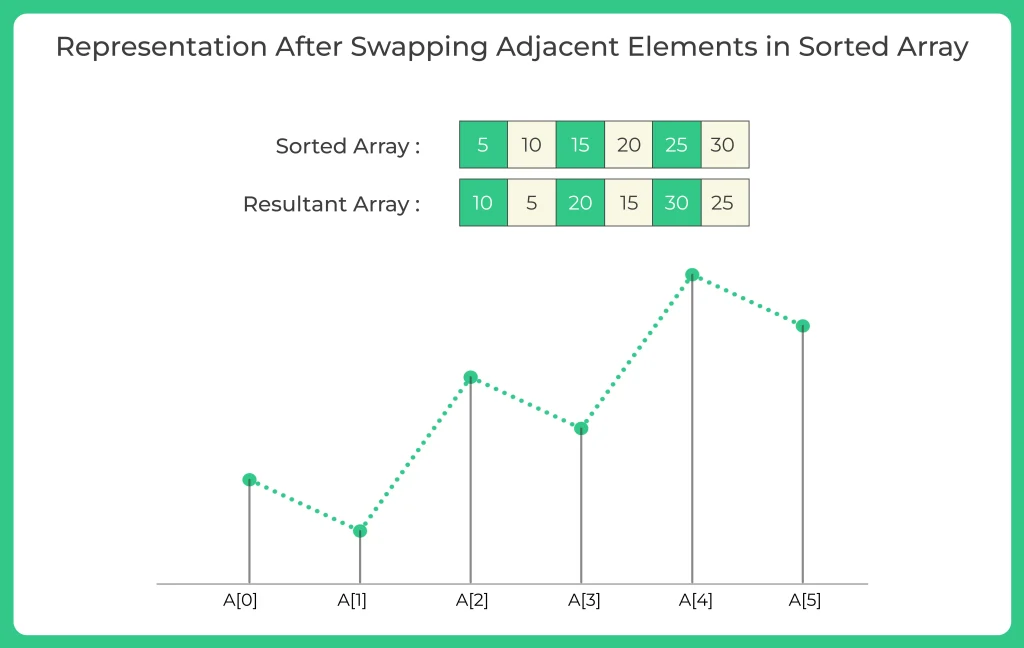
Method : 1 -Solution in C++ Programming Language
#include <iostream>
#include <algorithm> // For sorting
using namespace std;
int main() {
int array[] = {10, 49, 2, 1, 5, 23};
int n = sizeof(array) / sizeof(array[0]);
int temp;
for (int i = 0; i < n - 1; i++) {
for (int j = i + 1; j < n; j++) {
if (array[i] > array[j]) {
temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
}
for (int i = 0; i < n; i = i + 2) {
if (i < n - 1) {
temp = array[i];
array[i] = array[i + 1];
array[i + 1] = temp;
}
}
cout << "Array in Waveform Pattern: ";
for (int i = 0; i < n; i++) {
cout << array[i] << " ";
}
cout << endl;
return 0;
}
Output
Array in Waveform Pattern: 2 1 10 5 49 23
Method 2 : Incrementing the loop by 2
The above method using sorting has a time complexity of O(n log n), which may not be the most optimal solution for this problem. The Incrementing the loop by 2 method can indeed solve the problem in O(n) time complexity by making use of a single traversal of the array. Here are the steps for solving the problem in O(n) complexity:
Step 1: Traverse all even position elements of the array (i.e. elements at index 0, 2, 4, 6, etc.).
Step 2: For each even position element, check the following two conditions:
Condition 1: If the current element is smaller than the previous odd element (i.e. element at index (i-1)), swap the previous and current element.
Condition 2: If the current element is smaller than the next odd element (i.e. element at index (i+1)), swap the next and current element.
By following these steps, you can rearrange the array in O(n) time complexity, as you are traversing the array once and performing constant time swaps. This method is more efficient compared to the sorting method in terms of time complexity for this specific problem.
Method: 2 – Solution in C++ Programming Language
#include <iostream>
using namespace std;
int main ()
{
int array[] = { 10, 49, 2, 1, 5, 23 };
int n = sizeof (array) / sizeof (array[0]);
int temp;
for (int i = 0; i < n; i += 2)
{
if (i > 0 && array[i - 1] > array[i])
{
temp = array[i];
array[i] = array[i - 1];
array[i - 1] = temp;
}
if (i < n - 1 && array[i] < array[i + 1])
{
temp = array[i];
array[i] = array[i + 1];
array[i + 1] = temp;
}
}
for (int i = 0; i < n; i++)
{
cout << array[i] << " ";
}
return 0;
}
Output
49 2 10 1 23 5
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java






Login/Signup to comment