Majority Element in an Array in C++

April 28, 2023

Majority Element in array in C++ Language

In this page we will look into a coding question where we will learn how to find the element which occurs majority number of times in array in C++ Programming Language. There might be different approach to solve this question, one you will find here. If your approach is bit different post it onto the comment section.
Majority Element in an Array in C

Majority Element In An Array In C++

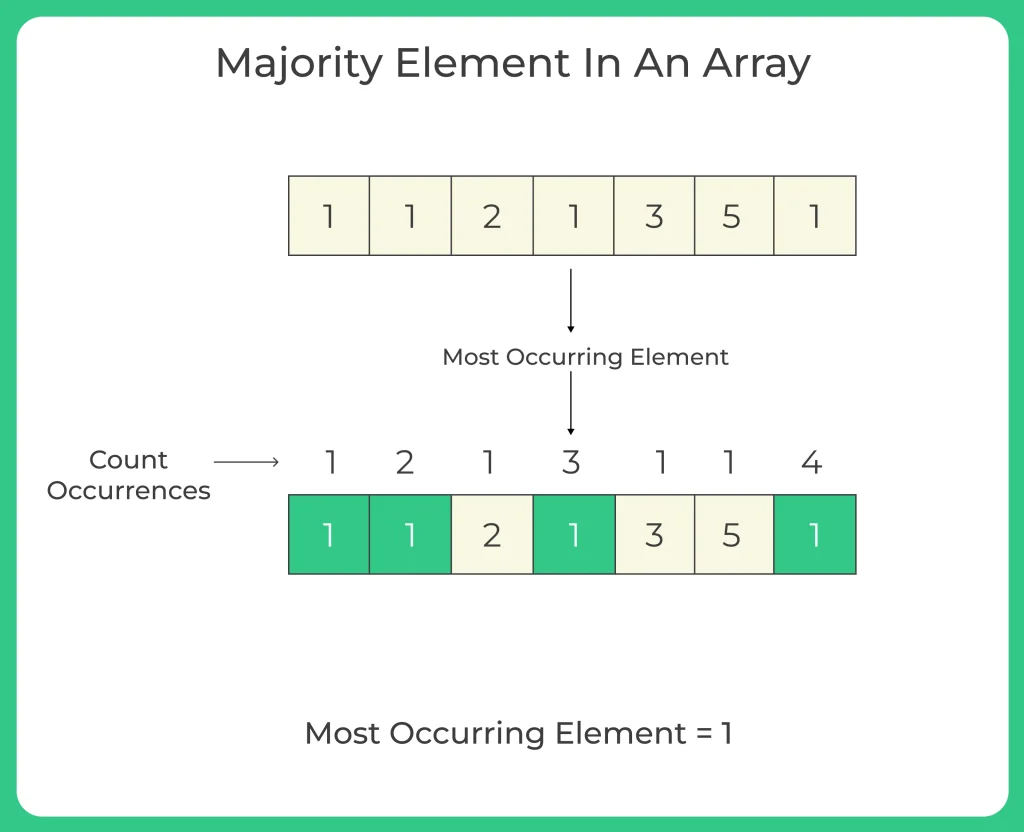
The Boyer-Moore Majority Vote Algorithm is a widely used algorithm for finding the majority element in an array. The majority element in an array in C++ is an element that appears more than n/2 times, where n is the size of the array.

This Algorithm is efficient with a time complexity of O(n) and a space complexity of O(1), as it uses constant extra space to maintain the candidate and count variables. It is a clever algorithm that leverages the properties of majority elements to find them efficiently in linear time.

Majority Element In An Array
DSA desktop gif
DSA mobile gif

Reverse an array or string

Sorting of Array

Array Rotation

Largest Sum Contigous SubArray

Boyer-Moore’s Voting Algorithm

Algorithm

  1. Initialize a variable candidate to store the candidate element, and set it to the first element of the array arr[0].
  2. Initialize a variable count to store the count of occurrences of the candidate element, and set it to 1.
  3. Iterate through the array arr from index 1 to n-1:
    • If count is 0, set the current element as the new candidate element and increment count to 1.
    • If the current element is equal to the candidate element, increment count by 1.
    • If the current element is not equal to the candidate element, decrement count by 1.
  4. Reset count to 0.
  5. Iterate through the array arr again to verify if the candidate element is a majority element:
    • If the current element is equal to the candidate element, increment count by 1.
  6. If count is greater than n/2, return the candidate element as the majority element.
  7. If no majority element is found, return -1.

Program for finding the element that occurs most time in an array

Run 
#include <iostream>
using namespace std;

int findMajorityElement (int arr[], int n)
{
  int candidate = 0;		// Candidate for majority element
  int count = 0;		// Count of occurrences of candidate element

  // Candidate selection phase
  for (int i = 0; i < n; i++)
    {
      if (count == 0)
	{
	  candidate = arr[i];	// Set current element as candidate
	  count = 1;
	}
      else if (arr[i] == candidate)
	{
	  count++;	
	}
      else
	{
	  count--;		
	}
    }

  // Verification phase
  count = 0;
  for (int i = 0; i < n; i++)
    {
      if (arr[i] == candidate)
	{
	  count++;		// Count occurrences of candidate element
	}
    }


  if (count > n / 2)
    {
      return candidate;
    }
  else
    {
      return -1;		// No majority element found
    }
}

int main ()
{
  int arr[] = { 3, 3, 4, 2, 4, 4, 2, 4, 4 };	// Example array
  int n = sizeof (arr) / sizeof (arr[0]);
  int majorityElement = findMajorityElement (arr, n);

  if (majorityElement != -1)
    {
      cout << "Majority element is: " << majorityElement << endl;
    }
  else
    {
      cout << "No majority element found" << endl;
    }

  return 0;
}

Output

Majority Element = 4

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion : C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal Line by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric – C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree- C | C++ | Java

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion :  C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal LIne by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric  C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree. C | C++ | Java