Tree Traversal : Breadth First Search (BFS)
Tree Traversal : Breadth First Search in Java
Here we will discuss Breadth First Search in Java, also known as Level Order Traversal, is one of the most important ways to traverse a tree. It visits nodes level by level, starting from the root.
This article explains BFS in a simple and beginner-friendly way, including its approach, algorithm, Java implementation, examples, and practical insights
Tree Traversal: Breadth First Search
BFS is a tree traversal technique where:
- Nodes are visited level by level
- All nodes at the same depth are processed before moving deeper
Example Tree:
1
/ \
2 3
/ \ \
4 5 6BFS Traversal:
1 → 2 → 3 → 4 → 5 → 6
Steps for Breadth First Search Tree Treaversal
Before practicing Breadth First Search in Java we will go through Step by step process for performing BFS alongwith comprehensive Algorithm explanation:
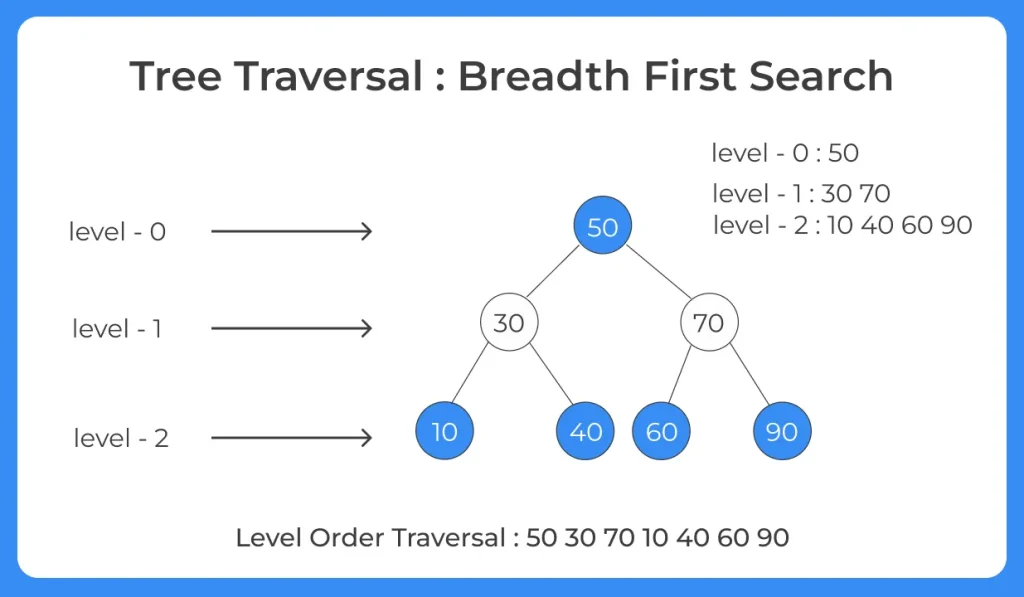
- Step 1 : Push the root i.e. 50 to the queue.
- Step 2 : Pop the element 50 from the queue and print it.
- Step 3 : Now, Add it’s left and right child i.e. add 30 and 70 to queue.
- Step 4 : Again pop the front element i.e. 30 from queue and print it .
- Step 5 : Add it’s left and right child i.e. 10 and 40 in the queue.
- Step 6 : Pop the element 70 from the queue and print it.
- Step 7 : add it’s left and right child i.e. 60 and 90.
Step 8 : Now pop all the elements from the queue and print them as there is no child of these elements.
Therefore the printing sequence will be 50 30 70 10 40 60 90 .
Algorithm for Breadth First Search in Java
Algorithm for performing Breadth First Search in Java programming:
- If root is null → return
- Create a queue
- Add root to queue
- While queue is not empty:
Remove node from queue
Print node value
If left child exists → add to queue
If right child exists → add to queue
Learn DSA
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Java Code for Breadth First Search (BFS)
import java.util.*;
class Node {
int data;
Node left, right;
Node(int value) {
data = value;
left = right = null;
}
}
public class BFSExample {
// BFS Traversal
public static void bfs(Node root) {
if (root == null) return;
Queue queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
Node current = queue.poll();
System.out.print(current.data + " ");
if (current.left != null) {
queue.add(current.left);
}
if (current.right != null) {
queue.add(current.right);
}
}
}
public static void main(String[] args) {
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.right = new Node(6);
System.out.print("BFS Traversal: ");
bfs(root);
}
}
Input
1
/ \
2 3
/ \ \
4 5 6
Output
BFS Traversal: 1 2 3 4 5 6
Space Complexity: O(n)
Common Insights on Breadth First Search in Java
- BFS is also called Level Order Traversal
- Uses queue instead of recursion
- Works for both trees and graphs
- Guarantees shortest path in unweighted graphs
- Easy to modify for level based problems
Best Practices:
- Always check for null root
- Use Queue interface instead of concrete class
- Prefer LinkedList or ArrayDeque for queue
- Avoid unnecessary object creation
- Use BFS when level information is important
Frequently Asked Questions
Answer:
It is a traversal technique where nodes are visited level by level using a queue.
Answer:
Because it processes all nodes at one level before moving to the next.
Answer:
A queue (FIFO) is used to maintain traversal order.
Answer:
It is O(n) since every node is visited once.
Answer:
Use BFS when shortest path or level wise traversal is required.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java
Login/Signup to comment