Preorder Tree Traversal of Binary Tree in C

February 28, 2023

Preorder Tree Traversal in Binary Tree in C
Direction (Inorder) Anti- Clockwise
Rule Center Left Right (CLR)

Understanding Preorder Traversal in Binary Tree in C

On this page we will discuss about Preorder Tree Traversal of Binary Tree in C . Preorder Tree traversal is where we try print the center most node first, i.e. the root node first and then we go ahead and print the left and then right node. The order of printing thus in anti-clockwise format.

Preorder Tree Traversal in Binary Tree in C Language

Implementing PreOrder Traversal

  • The direction of traversal for preorder is anti-clockwise
  • Rule followed is CLR (Center-Left-Right)

What we mean by above is that we try to visit the central node i.e. the root node first and once, there are no central node, we move to left node and right thus forming an anti-clockwise direction.

Check the example below –

Preorder Tree Traversal in Binary Tree in C PrepInsta

Explanation for PreOrder Traversal in Binary Tree

  • Start Traversing
  • Central Node (1): Print, Traverse left
  • Central Node (2): Print, Traverse left
  • Central Node (4) : Print Traverse Left
  • Left Node : Print Traverse Right
  • Recur up to Subtree of 2 Print Right node 5
  • The whole left subtree of Root node has been printed now go to right subtree of root node
  • Central Node (2) : Print, traverse Left
  • Central Node (6), print traverse left
  • No more left node traverse right print 10
  • Traverse right for 7 central node print, recur left
  • Print 11 (left node)
  • Print 12 (right node)
DSA desktop gif
DSA mobile gif

Priority Queue in C

Tree Traversals: Inorder Postorder Preorder

Inorder Tree Traversal in Binary Tree

Postorder Tree Traversal in Binary Tree

Preorder Tree Traversal without Recursion

Run 
// Program for tree traversal preorder in Binary Tree
#include<stdio.h>
#include<stdlib.h>
// We are creating struct for the binary tree below
struct node
{
  int data;
  struct node *left, *right;
};

// newNode function for initialisation of the newly created node
struct node *newNode (int item)
{
  struct node *temporary = (struct node *) malloc (sizeof (struct node));
  temporary->data = item;
  temporary->left = temporary->right = NULL;
  return temporary;
}

// Here we print the preorder recursively
void preorder (struct node *root)
{
  if (root != NULL)
    {
      printf ("%d ", root->data);
      preorder (root->left);
      preorder (root->right);
    }
}

// Basic Program to insert new node at the correct position in BST
struct node *insert (struct node *node, int data)
{
  /* When there no node in the tree(subtree) then create 
   and return new node using newNode function */
  if (node == NULL)
    return newNode (data);

  /* If not then we recur down the tree to find correct position for insertion */
  if (data < node->data)
    node->left = insert (node->left, data);
  else if (data > node->data)
    node->right = insert (node->right, data);

  return node;
}

int main ()
{
  /* What our binary search tree looks like really 
      9 
     / \ 
    7  14
   / \ / \ 
  5  8 11 16 */
  
  struct node *root = NULL;
  root = insert (root, 9);
  insert (root, 7);
  insert (root, 5);
  insert (root, 8);
  insert (root, 14);
  insert (root, 11);
  insert (root, 16);

  printf ("The preorder is :\n");
  preorder (root);

  return 0;
}

Output:

The preorder is :
9 7 5 8 14 11 16

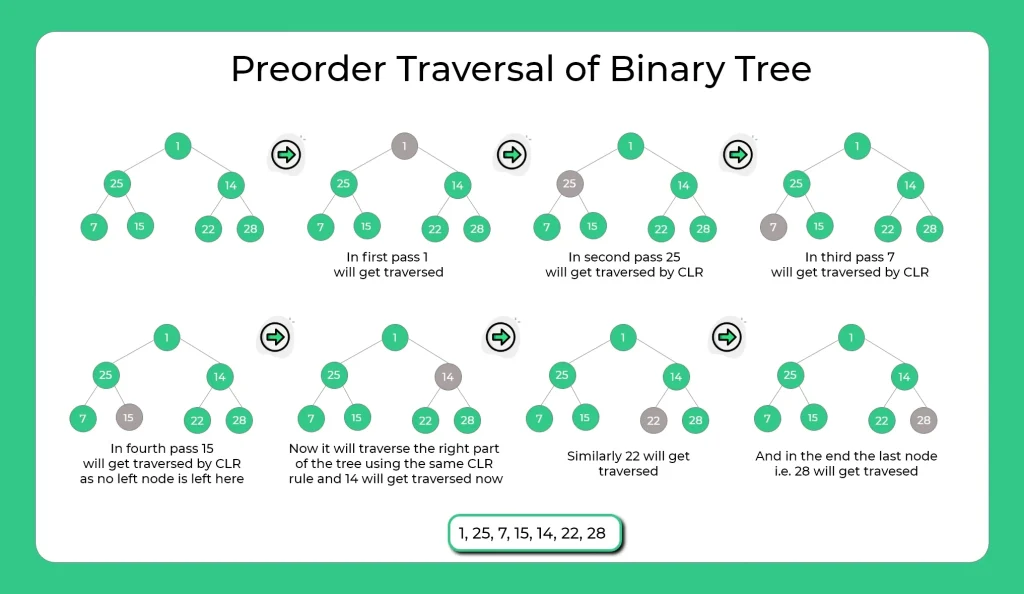
In the above example first root node i.e. 1 get traversed then, using the CLR rule it will traverse the left node i.e. 25 get traversed, then again CLR rule get applied and 7 will get traversed now no left node is left here so it will traverse right node i.e. 15 here , then 14 , then using CLR remaining 22 and 28 will get traversed. The image below will help you to understand in a better way.

Preorder Tree Traversal of Binary Tree in C

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion : C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal Line by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric – C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree- C | C++ | Java

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion :  C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal LIne by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric  C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree. C | C++ | Java