Postorder Tree Traversal in Binary Tree in C

| Direction (Inorder) | Anti Clock |
| Rule | Left Right Center (LRC) |
Postorder Traversal of the Tree in C
Postorder Tree Traversal in Binary Tree in C is one of the most frequently used tree traversals, in such traversal we try to print the left most root first. Let us see how post order tree traversals work –
Postorder Tree Traversal in Binary Tree in C Language
Working of PostOrder Algorithm
- We traverse in Anti Clock wise Direction
- Rule followed is LRC(Left-Right-Center)
Which means that we try to visit the leftmost node of the tree first and then its subtree’s right node and then center/middle node and keep on doing the same iteratively.
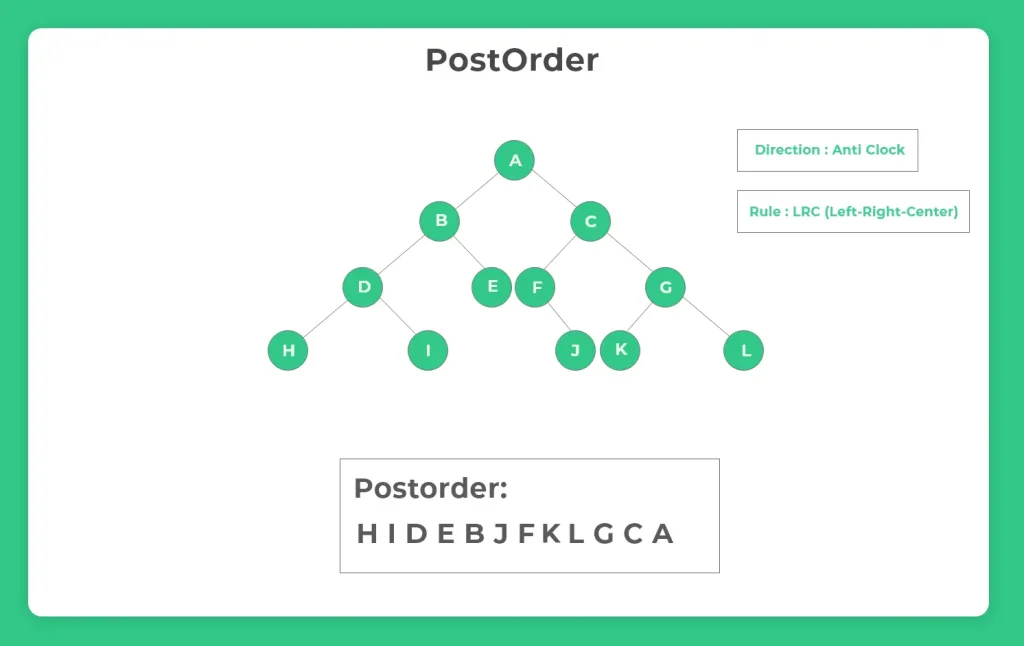
Working for the above image for Postorder traversal
We traverse the tree and try to go to the left most node- Here, Leftmost item is 8, right item : 9, middle item : 4 (Now recursive moving in the tree)
- Print 8 9 4
- Leftmost item is 4 (However, we’ve visited it already), so now, right item is 5 then middle item : 2
- Print 5 2
- The left side of the tree is done, moving to right side of the tree
- (In right subtree) The leftmost item: NULL, and its right item is: 10, middle item: 10 (Move up the tree)
- Print 10 6
- Central item, 3, however 3 has child elements, so we try to visit its subtree’s
- Now, we come across 7, which still has a subtree so we recur down the tree
- The left node of 7 is last node in the tree and left most, its right sibling: 12, middle: 7
- Print: 11 12 7
- Now, recurring up, whole subtree (Both left & right of 3 is printed so
- Print 4
Algorithm for Postorder Traversal
Postorder(root)- Traverse the left sub-tree, (recursively call postorder(root -> left).
- Traverse the right sub-tree, (recursively call postorder(root -> right).
- Visit and print the root node.
Run
// Program for tree traversal postorder in Binary Tree
#include<stdio.h>
#include<stdlib.h>
// We are creating struct for the binary tree below
struct node
{
int data;
struct node *left, *right;
};
// newNode function for initialisation of the newly created node
struct node *newNode (int item)
{
struct node *temporary = (struct node *) malloc (sizeof (struct node));
temporary->data = item;
temporary->left = temporary->right = NULL;
return temporary;
}
// Here we print the postorder recursively
void postorder (struct node *root)
{
if (root != NULL)
{
postorder (root->left);
postorder (root->right);
printf ("%d ", root->data);
}
}
// Basic Program to insert new node at the correct position in BST
struct node *insert (struct node *node, int data)
{
/* When there no node in the tree(subtree) then create
and return new node using newNode function */
if (node == NULL)
return newNode (data);
/* If not then we recur down the tree to find correct position for insertion */
if (data < node->data)
node->left = insert (node->left, data);
else if (data > node->data)
node->right = insert (node->right, data);
return node;
}
int main ()
{
/* What our binary search tree looks like really
9
/ \
7 14
/ \ / \
5 8 11 16 */
struct node *root = NULL;
root = insert (root, 9);
insert (root, 7);
insert (root, 5);
insert (root, 8);
insert (root, 14);
insert (root, 11);
insert (root, 16);
printf ("The postorder is :\n");
postorder (root);
return 0;
}
Output:
The postorder is : 5 8 7 11 16 14 9
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java






Login/Signup to comment