Programming
Aptitude
Syllabus
Interview Preparation
Interview Exp.
Off Campus
0Bubble Sort in C
Bubble Sort in C
Sorting is the process of arranging the data in some logical order. Bubble sort is an algorithm to sort various linear data structures.
The logical order can be ascending and descending in the case of numeric values or dictionary order in the case of alphanumeric values.
- Bubble Sort is a very simple and easy to implement sorting technique.
- In the bubble sort technique, each pair of element is compared.
- Elements are swapped if they are not in order.
- The worst-case complexity of bubble sort is O(n2).
| Time Complexity | O(n2) |
| Best Case | O(n) |
| Worst Case | O(n2) |
| Space Complexity | O(1) |
| Avg. Comparisons | n(n-1)/2 |
Implementation of Bubble Sort
The algorithm works on the principle (For ascending order)
- Linearly traverse an array
- Start from the leftmost item
- If left item is greater than its right item swap them
That is arr[i] > arr[i+1] swap them
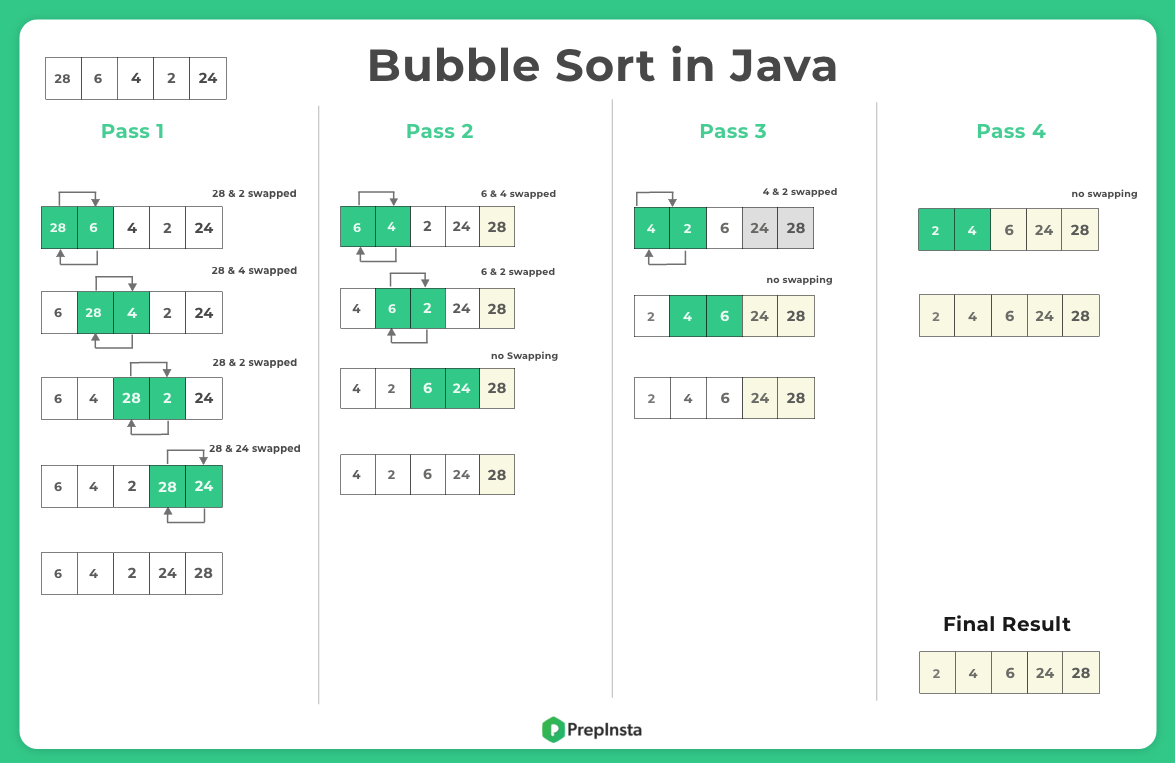
Let’s take an example, we have a list of number stored in array
Pass 1
- ( 28 6 4 2 24 ) -> ( 6 28 4 2 24 ) : Swapped 28 & 6 since 28 > 6
- ( 6 28 4 2 24 ) -> ( 6 4 28 2 24 ) : Swapped 28 & 4 since 28 > 4
- ( 6 4 28 2 24 ) -> ( 6 4 2 28 24 ) : Swapped 28 & 2 since 28 > 2
- ( 6 4 2 28 24 ) -> ( 6 4 2 24 28 ) : Swapped 28 & 24 since 28 > 24
As you can see in pass 1 we got the largest element at the end of the array so that part is already sorted. Which is why its called bubble sort
- Like in a soda drink the largest bubble traverse to the stop first
- Here the largest item traversed to right first
See more iterations in the image below –
Code of Bubble Sort
- Time Complexity: O(n)
- Space Complexity: O(1)
#include <stdio.h>
// Function to print array
void display(int arr[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", arr[i]);
printf("\n");
}
// Main function to run the program
int main()
{
int array[] = {5, 3, 1, 9, 8, 2, 4,7};
int size = sizeof(array)/sizeof(array[0]);
printf("Before bubble sort: \n");
display(array, size);
int i, j, temp;
for (i = 0; i < size-1; i++){
// Since, after each iteration right-most i elements are sorted
for (j = 0; j < size-i-1; j++)
if (array[j] > array[j+1])
{
temp = array[j]; // swap the element
array[j] = array[j+1];
array[j+1] = temp;
}
}
printf("After bubble sort: \n");
display(array, size);
return 0;
}#include <stdio.h>
void swap(int *var1, int *var2)
{
int temp = *var1;
*var1 = *var2;
*var2 = temp;
}
// Here we are implementing bubbleSort
void bubbleSort(int arr[], int n)
{
int i, j;
for (i = 0; i < n-1; i++)
// Since, after each iteration rightmost i elements are sorted
for (j = 0; j < n-i-1; j++)
if (arr[j] > arr[j+1])
swap(&arr[j], &arr[j+1]);
}
/* Function to print array */
void display(int arr[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", arr[i]);
printf("\n");
}
// Main function to run the program
int main()
{
int array[] = {5, 3, 1, 9, 8, 2, 4,7};
int size = sizeof(array)/sizeof(array[0]);
printf("Before bubble sort: \n");
display(array, size);
bubbleSort(array, size);
printf("After bubble sort: \n");
display(array, size);
return 0;
}Output
After Sorted Element List
Before bubble sort
5 3 1 9 8 2 4 7
After bubble sort:
1 2 3 4 5 7 8 9
Method 2
The above code isn’t optimized for if the array is already sorted or nearly sorted.
Even if the array is sorted in the above (method 1) code the time complexity for the best case will still be O(N2).
- This can be resolved using a flag variable that changes its value if there was no swapping in any of the passes.
- This reduces the best case time complexity (when the array is already sorted) to O(N)
This array is already sorted still the above bubble sort code will run all the passes and iterations anyways.
arr[] = {10, 20, 30, 100, 50}
Even for this array which has one single item '100' out of place will get sorted in the first pass itself. Still, all passes and iterations will run.
This can be resolved by changing the code as below by introducing a flag variable
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Code Method 2
If there is any pass where no swap happens, do not implement any further passes since the array is already sorted.
#include <stdio.h>
void swap(int *var1, int *var2)
{
int temp = *var1;
*var1 = *var2;
*var2 = temp;
}
// Here we are implementing bubbleSort
void bubbleSort(int arr[], int n)
{
int i, j;
for (i = 0; i < n-1; i++){
// initializing swapped to 0 (no swaps happenned yet)
int swapped = 0;
// Since, after each iteration righmost i elements are sorted
for (j = 0; j < n-i-1; j++) {
if (arr[j] > arr[j+1])
{
swap(&arr[j], &arr[j+1]);
// change swap value as swap has happenned
swapped = 1;
}
}
// if no swaps happen stop don't impliment further passes/iterations
if(!swapped)
break;
}
}
/* Function to print array */
void display(int arr[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", arr[i]);
printf("\n");
}
// Main function to run the program
int main()
{
int array[] = {10, 20, 30, 40, 50};
int size = sizeof(array)/sizeof(array[0]);
printf("Before bubble sort: \n");
display(array, size);
bubbleSort(array, size);
printf("After bubble sort: \n");
display(array, size);
return 0;
}Output
Before bubble sort: 10 20 30 40 50 After bubble sort: 10 20 30 40 50
Performance-Based Analysis of Bubble Sort Algorithm
Pros
- Easy to implement
- Cool to implement
- Gives the largest value of the array in the first iteration itself.
- Or the smallest value of array in the first iteration itself (Minor tweak in implementation)
- No demand for large amounts of memory for operation
Cons
- Noob (Bad) algorithm 😀
- Very horrible time complexity of O(n2)
Interesting Facts
- Average and worst-case time complexity: o(n2)
- Best case time complexity: n when the array is already sorted.
- Worst case: when the array is reverse sorted.
Number of comparisons in Bubble sort is reduces by 1 in each pass.
Example – For array size 5,
- In Pass 1: 4 comparisons
- In Pass 2: 3 comparisons
- In Pass 3: 2 comparisons
- In Pass 4: 1 comparison
Thus, for n sized array the total number of comparisons, therefore, is (n – 1) + (n – 2)…(2) + (1) = n(n – 1)/2
Time Complexity
For Bubble Search
Best
Ω(n)
Average
Θ(n2)
Worst
O(n2)
Space Complexity
O(1)
Sorting
Sorting algorithms are easy to learn but are really important for college semester exams and companies offering package between 3 – 6 LPA would ask direct searching questions in online test/ interviews.
Login/Signup to comment