Find the Armstrong Numbers in a given Interval in C++
Find the Armstrong Numbers in a given Range in C++
Given two integers high and low for limits as inputs, the objective is to write a code to Find the Armstrong Numbers in a given Interval in C++.
Output : 153 370 371

Find the Armstrong Numbers in a given Interval in C++
Given two integer inputs as high and low, the objective is to find all the Armstrong Numbers that falls under the limits [Low,High] interval. Before Going into the Explanation let’s understand the problem.
Example 1:
Input : 100 400
Output :153 370 371
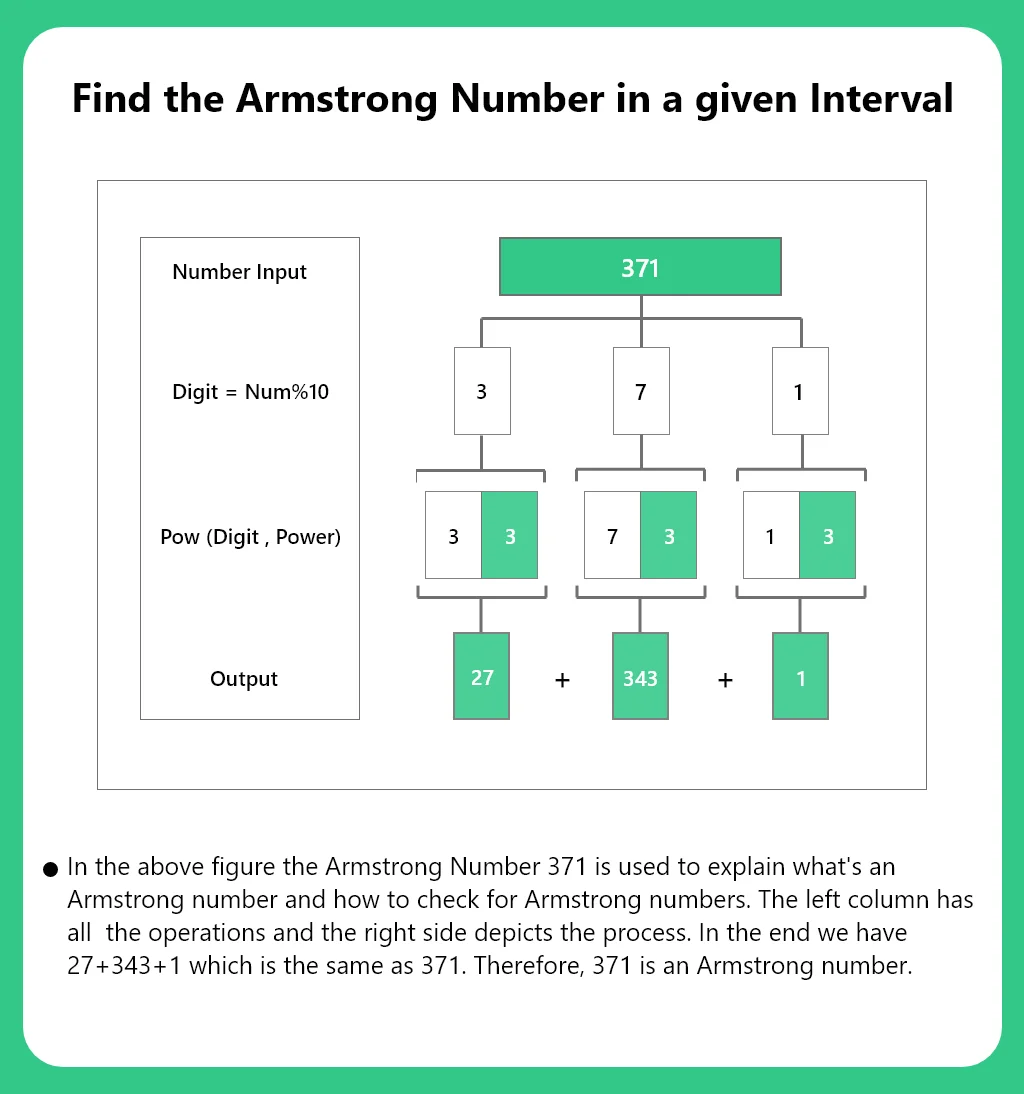
Explanation : 100 and 400 are given
two integers.(interval)
153 = 1*1*1 + 5*5*5 + 3*3*3
= 1 + 125 + 27
= 153
370 = 3*3*3 + 7*7*7 + 0
= 27 + 343
= 370
371 = 3*3*3 + 7*7*7 + 1*1*1
= 27 + 343 +1
= 371
Let’s take the above example and try to understand the definition of Armstrong Numbers, The input for the code as mentioned is the range within which we search for the Armstrong Numbers. The Armstrong Number we Found were 153, 370 and 371. According to the Definition an Armstrong number is any number that can be expressed an the sum of it’s digits raised to the power of it’s length. And as the above mentioned numbers satisfy the conditions, They are printed out as Armstrong Numbers lying with the range [100,400].
Find the Armstrong Numbers in a given Range in C++
As mentioned above, given two integer inputs as limits or range, write a C++ code to find all the Armstrong Numbers lying in the given range. In order to do so we have two different approaches,
- Method 1: Using Order function
- Method 2: Without Order function
We’ll discuss these approaches in depth in the sections below.
Method 1: Using Order Function
In this method we define the order() function which takes in an integer value x and returns the number of digits of the number.
C++ Code
#include<bits/stdc++.h>
#include<math.h>
using namespace std;
// number of digits in a number is order
int order(int x)
{
int len = 0;
while (x)
{
len++;
x = x/10;
}
return len;
}
void armstrong(int low, int high){
for(int num = low; num <= high; num++){
int sum = 0, temp, digit, len;
temp = num;
// function to get order(length)
len = order(num);
// loop to extract digit, find cube & add to sum
while(temp != 0)
{
// extract digit
digit = temp % 10;
// add power to sum
sum = sum + pow(digit,len);;
temp /= 10;
};
if(sum == num)
cout << num << " ";
}
}
// Driver Code
int main ()
{
//variables initialization
int low = 100, high = 400;
// get armstrong numbers
armstrong(low, high);
return 0;
}
Output
153 370 371
Algorithm
The objective of the above code is to find all the Armstrong Numbers in the given input interval in C++. In this Method we’ll use a user defined function order() to solve the problem.
The algorithm for the above code is as follows:
- Include the required header files.
- Define a Function order() which takes a number as argument and returns it’s length.
- Define another function armstrong() which accepts the intervals low and high as arguments and prints the Armstrong numbers along the way.
- Using for loop we’ll check for each number if it’s an Armstrong Number.
- We’ll get the length of the number using the order function.
- Using while loop we’ll carry on the process which is shown in the image above.
- check if the sum of the digits raised to the power of it’s length is equal to the number itself.
- If true, print the number else keep checking.
The output for the above code is all the Armstrong numbers in the given interval.
Method 2: Without using Order Function
In this method we will perform both length calculation and breaking down of the number input within the actual function.
Python Code
#include <bits/stdc++.h>
using namespace std;
// Prints Armstrong Numbers in given range
void findArmstrong(int low, int high)
{
for (int i = low+1; i < high; ++i) {
// number of digits calculation
int x = i;
int n = 0;
while (x != 0) {
x /= 10;
++n;
}
// compute sum of nth power of
// its digits
int pow_sum = 0;
x = i;
while (x != 0) {
int digit = x % 10;
pow_sum += pow(digit, n);
x /= 10;
}
// checks if number i is equal to the
// sum of nth power of its digits
if (pow_sum == i)
cout << i << " ";
}
}
// Driver code
int main()
{
int num1 = 100;
int num2 = 400;
findArmstrong(num1, num2);
cout << '\n';
return 0;
}
Output
153 370 371
Algorithm
The objective of the above code is to find all the Armstrong Numbers in the given input interval in C++.
The algorithm for the above code is as follows:
- Include the required header files.
- Define another function findArmstrong() which accepts the intervals low and high as arguments and prints the Armstrong numbers along the way.
- Using for loop we’ll check for each number if it’s an Armstrong Number.
- We’ll get the length of the number using a while loop.
- Using while loop we’ll carry on the process which is shown in the image above.
- check if the sum of the digits raised to the power of it’s length is equal to the number itself.
- If true, print the number else keep checking.
The output for the above code is all the Armstrong numbers in the given interval.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
- Positive or Negative number: C | C++ | Java | Python
- Even or Odd number: C | C++ | Java | Python
- Sum of First N Natural numbers: C | C++ | Java | Python
- Sum of N natural numbers: C | C++ | Java | Python
- Sum of numbers in a given range: C | C++ | Java | Python
- Greatest of two numbers: C | C++ | Java | Python
- Greatest of the Three numbers: C | C++ | Java | Python
- Leap year or not: C | C++ | Java | Python
- Prime number: C | C++ | Java | Python
- Prime number within a given range: C | C++ | Java | Python
- Sum of digits of a number: C | C++ | Java | Python
- Reverse of a number : C | C++ | Java | Python
- Palindrome number: C | C++ | Java | Python
- Armstrong number : C | C++ | Java | Python
- Armstrong number in a given range : C | C++ | Java | Python
- Fibonacci Series upto nth term : C | C++ | Java | Python
- Find the Nth Term of the Fibonacci Series : C | C++ | Java | Python
- Factorial of a number : C | C++ | Java | Python
- Power of a number : C | C++ | Java | Python
- Factor of a number : C | C++ | Java | Python
- Strong number : C | C++ | Java | Python
- Perfect number : C | C++ | Java | Python
- Automorphic number : C | C++ | Java | Python
- Harshad number : C | C++ | Java | Python
- Abundant number : C| C++ | Java | Python
- Friendly pair : C | C++ | Java | Python







Login/Signup to comment