Finding the Nth Term of the Fibonacci Series in C++

September 27, 2022

What is a Fibonacci Series and Find the Nth Term of the Fibonacci Series?

The Fibonacci numbers, commonly denoted F(N) form a sequence, called the Fibonacci series, such that each number is the sum of the two preceding ones, starting from 0 and 1.

That is,
F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1.

Given N, calculate F(N).

Example 1:
Input:n = 2
Output: 1
Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1
Finding the Nth term of the Fibonacci Series

Finding the Nth Term of the Fibonacci Series

In mathematics, the Fibonacci numbers, commonly denoted Fₙ form a sequence, the Fibonacci sequence, in which each number is the sum of the two preceding ones. The sequence commonly starts from 0 and 1, although some authors omit the initial terms and start the sequence from 1 and 1 or from 1 and 2.

The Series has two seed values F0 = 0 and F1 = 1. Starting with the seed values we keep adding and changing the “a” and “b” values which initially are a = F0 and b = F1.

The General formula for the Fibonacci series is

  • Fn = Fn-1 + Fn-2

Where Fn is the Output.

Finding Nth term in a Fibonacci Series

C++ Code

Method 1: Using Recursion

Run 
//Fibonacci Series using Recursion
#include<bits/stdc++.h>
using namespace std;
 
int F(int N)
{
    if (N <= 1)
       {
        return N;
       }
       
    return F(N-1) + F(N-2);
}
 
int main ()
{
    int N = 5;
    cout << F(N);
    return 0;
}

Output

5

Explanation

The objective is to recursively add the seed values and keep on adding forming a Fibonacci Series until the input index is reached.

The algorithm for the above code is as follows:

  1. Declare an int function F(int N) that takes the index+1 value as an argument.
  2. Check if the integer N is lesser or equal to 1. If yes return the integer N.
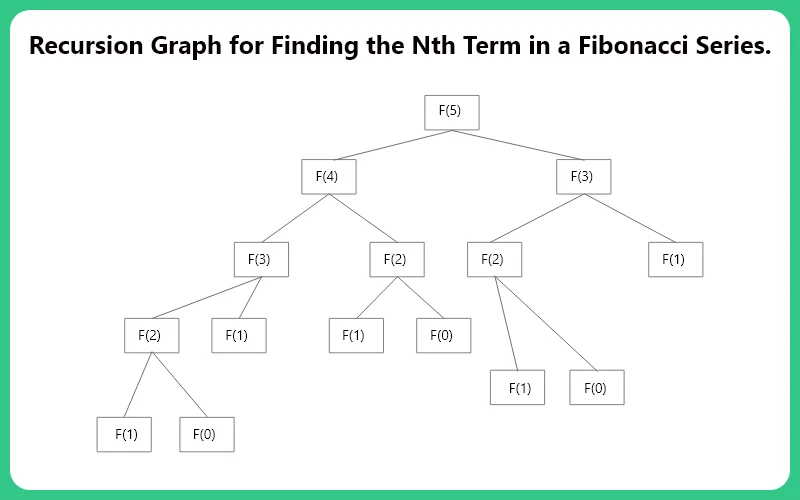
  3. In the return statement call the function F(N) recursively. This process is shown in the recursion tree.
  4. Print the output after calling the F(5) function using cout command.

The output for the above code is the number from the Fibonacci series at the given index N-1.  

 

Fibonacci Series Using Recurssion

Method 2: Using Space Optimization

C++ Code

Run 
// Fibonacci Series using Space Optimized Method
#include<bits/stdc++.h>
using namespace std;
 
int F(int N)
{
    int a = 0, b = 1, c, i;
    if( N == 0)
        return a;
    for(i = 2; i <= N; i++)
    {
       c = a + b;
       a = b;
       b = c;
    }
    return b;
}
 
// Driver code
int main()
{
    int N = 5;
     
    cout << F(N);
    return 0;
}

Output

5

Explanation

The objective is to add the seed values and keep on adding forming a Fibonacci Series until the input index is reached. Then Print out the Value at the given index of the Fibonacci series. 

The algorithm for the above code is as follows:

  1. Declare an integer function F(int N) which takes an integer argument N.
  2. Initialize a and b as seed values and declare an integer variable c for calculation and i for iteration.
  3. Check if N==0, if True return 0.
  4. Iterate through using a for loop with the condition i<=N.
  5. Perform F(N) = F(N-1) + F(N-2).
  6. Return the value of F(N) i.e “b”.
  7. Print the Output using cout command and call the function F(5).

The output for the above code is the number from the Fibonacci series at the given index N-1.  

Fibonacci Series Formula
  • Formula for Finding the Nth Term of the Fibonacci Series.

Armstrong number in a given range

Fibonacci Series upto nth term

Find the Nth Term of the Fibonacci Series

Factorial of a number

Power of a number

Factor of a number

Method 3: Using Matrix Multiplication

C++ Code

Run 
// Using Matrix
#include<bits/stdc++.h>
using namespace std;

void multiply(int fibonacci[2][2], int Mat[2][2]);

void power(int fibonacci[2][2], int N);

int F(int N)
{
	int fibonacci[2][2] = { { 1, 1 }, { 1, 0 } };
	
	if (N == 0)
		return 0;
		
	power(fibonacci, N - 1);
	
	return fibonacci[0][0];
}

void multiply(int fibonacci[2][2], int Mat[2][2])
{
	int x = fibonacci[0][0] * Mat[0][0] +
			fibonacci[0][1] * Mat[1][0];
	int y = fibonacci[0][0] * Mat[0][1] +
			fibonacci[0][1] * Mat[1][1];
	int z = fibonacci[1][0] * Mat[0][0] +
			fibonacci[1][1] * Mat[1][0];
	int w = fibonacci[1][0] * Mat[0][1] +
			fibonacci[1][1] * Mat[1][1];
	
	fibonacci[0][0] = x;
	fibonacci[0][1] = y;
	fibonacci[1][0] = z;
	fibonacci[1][1] = w;
}

void power(int fibonacci[2][2], int N)
{
	int i;
	int Mat[2][2] = { { 1, 1 }, { 1, 0 } };
	
	for(i = 2; i <= N; i++)
		multiply(fibonacci, Mat);
}

// Driver code
int main()
{
	int N = 5;
	
	cout << " " << F(N);
	
	return 0;
}

Output

5

Explanation

The objective is to use matrix multiplication to form a Fibonacci Series using the given Formula and print out the value at the given index of the Fibonacci series.

The algorithm for the above code is as follows:

  1. Declare an integer function F( int N) which accepts integer values N as argument.
  2. Create a 2D integer matrix or dimensions 2×2 and initialize it.
  3. Check if N==0, if True return 0.
  4. Using Matrix Multiplication raise the matrix fibonacci[2][2] to the power of N.
  5. Return the First element of the matrix i.e fibonacci[0][0].
  6. Print the output using cout command and call the function F(5).

The output for the above code is the number from the Fibonacci series at the given index N-1.

Fibonacci Series
  • Formula for Finding the Nth Element of a Fibonacci series using Matrix Multiplication.

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime