Programming
Aptitude
Syllabus
Interview Preparation
Interview Exp.
Off Campus
0
Notifications Mark All Read
- Login
- Get Prime
0
Python Program to Find Maximum Scalar Product of Two Vectors in an Array
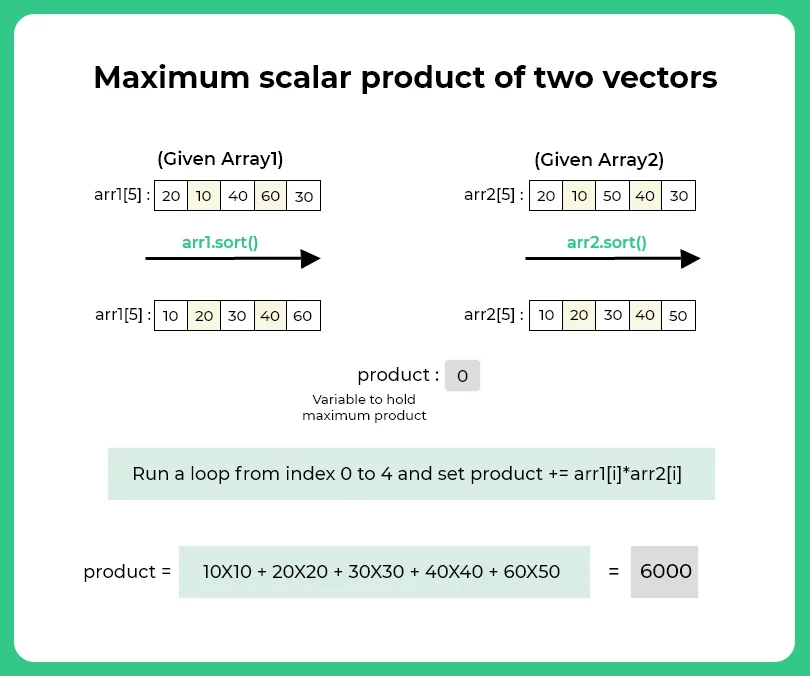
Maximum Scalar Product of two Vectors in Python
Here, in this page we will discuss the program to find the maximum scalar product of two vectors in python programming language. Scalar product is also known as dot product. We are given with two vectors and need to print the maximum dot product obtained.
Example
Input :arr1[4] = [10, 30, 40, 20]arr2[4] = [2, 4, 5, 1]
Output : 370
Explanation : 10*1 + 20*2 + 30*4 + 40*5 = 370
Methods Discussed :
- Method 1 : Without Using Inbuilt sort() function.
- Method 2 : Using sort() function.
Method 1 :
- Sort the first and second array in ascending order.
- Declare a variable say product = 0.
- Run a loop from index 0 to n
- Set product += (arrr1[i]*arr2[i])
- After complete iteration print product.
Time and Space Complexity :
- Time Complexity : O(n2)
- Space Complexity : O(1)
Method 1 : Code in Python
Run
arr1 = [1, 2, 6, 3, 7]
arr2 = [10, 7, 45, 3, 7]
n = len(arr1)
#Sort arr1 in ascending order
for i in range(n):
for j in range(i+1, n):
if arr1[i]>arr1[j] :
arr1[i], arr1[j] = arr1[j], arr1[i]
#Sort arr2 in ascending order
for i in range(n):
for j in range(i+1, n):
if arr2[i]>arr2[j] :
arr2[i], arr2[j] = arr2[j], arr2[i]
product = 0
for i in range(n):
product += arr1[i]*arr2[i]
print(product)
Output
413
Method 2 :
In this method we will use inbuilt sort function to sort the array.
- For, sorting arr1 in ascending order, use arr1.sort()
- For, sorting arr2 in ascending order, use
arr2.sort().
sort() function
The sort() method is a built-in Python method that, by default, sorts the list in ascending order.However, you can modify the order from ascending to descending by specifying the sorting criteria.
Method 2 : Code in Python
Run
arr1 = [1, 2, 6, 3, 7] arr2 = [10, 7, 45, 3, 7] n = len(arr1) #Sort arr1 in ascending order arr1.sort() #Sort arr2 in ascending order arr2.sort() product = 0 for i in range(n): product += arr1[i]*arr2[i] print(product)
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Output:
413
Login/Signup to comment
//Try this in C:
#include
int InsertionSort(int *,int);
int main()
{
int arrX[50],arrY[50],n,i,j,total=0;
printf(“Enter the length of array: “);
scanf(“%d”,&n);
printf(“Enter the value in arrayX: “);
for(i=0;i<n;i++)
{
scanf("%d",&arrX[i]);
}
printf("Enter the value in arrayY: ");
for(i=0;i<n;i++)
{
scanf("%d",&arrY[i]);
}
InsertionSort(arrX,n);
InsertionSort(arrY,n);
for(i=0;i<n;i++)
{
total=total+arrX[i]*arrY[i];
}
printf("The result is: %d",total);
return 0;
}
int InsertionSort(int *arr,int n)
{
int temp,pos,i;
for(i=1;i<n;i++)
{
temp=arr[i];
pos=i-1;
while(temp=0)
{
arr[pos+1]=arr[pos];
pos=pos-1;
}
arr[pos+1]=temp;
}
return 0;
}