Programming
Aptitude
Syllabus
Interview Preparation
Interview Exp.
Off Campus
0
Notifications Mark All Read
- Login
- Get Prime
0
Insertion in B-Tree
B-Trees
In this article, we will learn Introduction to B-Trees. B-Tree is a self-balancing search tree. The main idea of using B-Trees is to reduce the number of disk accesses. The height of B-Trees is kept low by putting maximum possible keys in a B-Tree node.
Insertion in B-Tree
In this article, we will learn about Insertion in B-Tree.
- In a B-Tree new key is always inserted at the leaf node.
- In B-tree, we start from the root and traverse down till we reach a leaf node.
- After we reach a leaf node, we insert the key in that leaf node.
- In this technique, we have a predefined range on the number of keys that a node can contain.
- So before inserting a key to the node, we make sure that the node has extra space.
- For this,we use an operation called
splitChild()that is used to split a child of a node.
Algorithm for insertion in B-Tree
Step 1: Initialize x as root.
Step 2: While x is not leaf, do following
- Find the child of x that is going to be traversed next. Let the child be y.
- If y is not full, change x to point to y.
- If y is full, split it and change x to point to one of the two parts of y. If k is smaller than mid key in y, then set x as the first part of y else second part of y. When we split y, we move a key from y to its parent x.
Step 3: The loop in step 2 stops when x is leaf. x must have space for 1 extra key as we have been splitting all nodes in advance. So simply insert key to x.
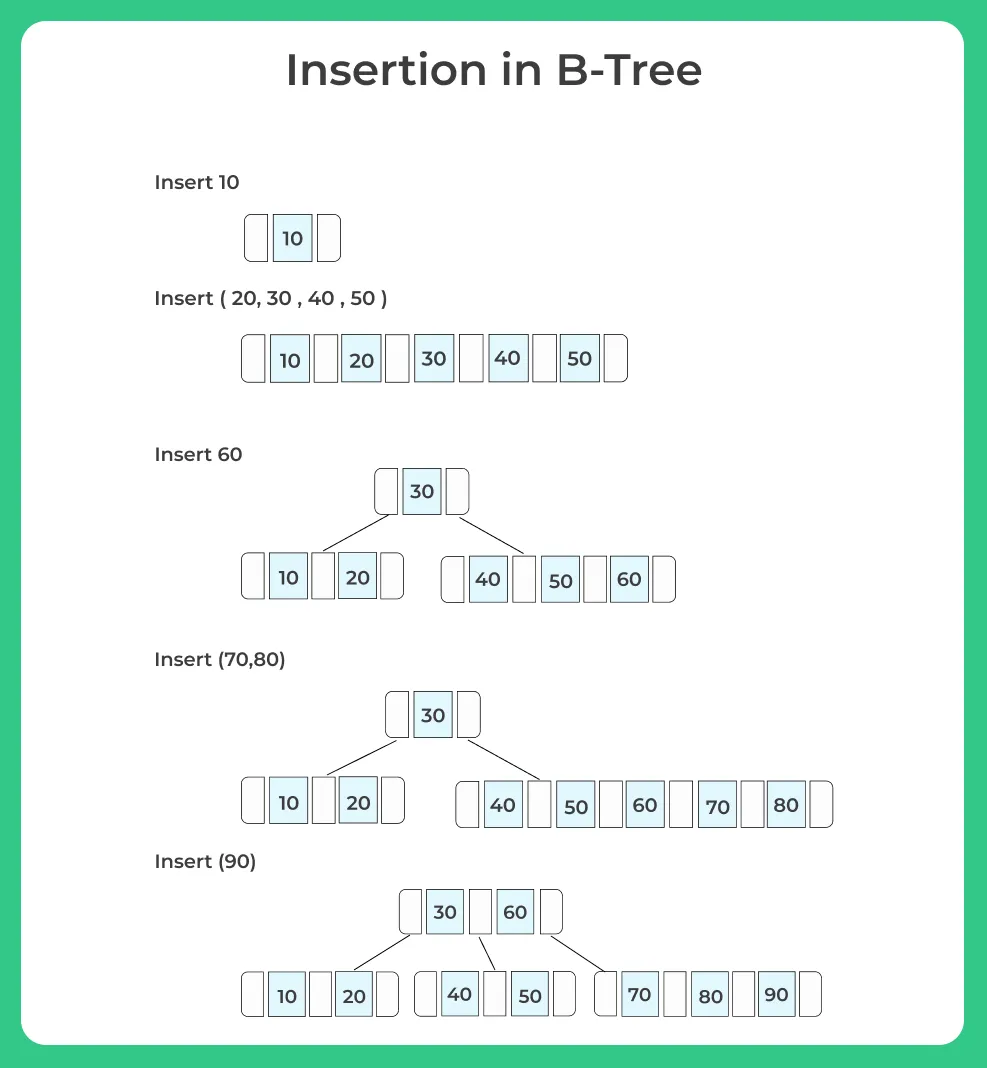
Example
Consider a sequence of integers 10, 20, 30, 40, 50, 60, 70, 80 and 90 to be inserted in an initially empty B-Tree with minimum degree n=3
Step1:Initially root is NULL. Let us first insert 10.
Step2: Now insert 20, 30, 40 and 50. They all will be inserted in root because the maximum number of keys a node can accommodate is 2n–1 which is 5.
Step3: Now insert 60. As root node is full, it will first split into two, then 60 will be inserted into the appropriate child.
Step4: Let us now insert 70 and 80. These new keys will be inserted into the appropriate leaf without any split.
Step5: Let us now insert 90. This insertion will cause a split. The middle key will go up to the parent.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Login/Signup to comment