0
Notifications Mark All Read
- Login
- Get Prime
Relational Algebra in DBMS
What is Relational Algebra in DBMS?
On this page, we will learn about Relational Algebra in DBMS.
Relational Algebra in DBMS is a query language which is procedural in nature, both of its input and output are relations. The theoretical foundations of relational databases and SQL is provided by Relational Algebra.

Relational Algebra in DBMS
Following operations can be applied via relational algebra –
- Select
- Project
- Union
- Set Different
- Cartesian product
- Rename
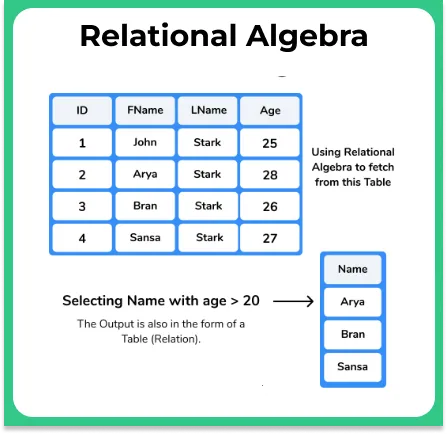
Select Operation (σ)
Use – Fetching rows (tuples) from a table, which satisfied a given condition.
Notation – σp(r)
Breakdown –
σrepresents select predicaterfor relationpfor proposition logics like –− =, ≠, ≥, < , >, ≤. with us of connectors likeOR,AND, orNOT
Like we used in the earlier example in the image above, of selecting rows for people who had age > 25 and give results in Fname format.

Example 1
- Query –
σage > 25 (Student)σ(select predicate)r(relation) – Employeep(proposition logic) – age >25- Result – returning the list of students with age greater than 25.
- In SQL – select * from Student where age > 25

Example 2
- Query
σage > 25 and Fname = 'Arya' (Student)σ(select predicate)r(relation) – Employeep(proposition logic) – age >25 and Fname = ‘Arya’- Result – returning the list of students with age greater than 25 and Fname equals to arya
- In SQL – select * from Student where age > 25 & Fname = ‘Arya’
- Query

Example 3
- Query
σLname = 'Stark' (Student)σ(select predicate)r(relation) – Employeep(proposition logic) – Lname = ‘Stark’- Result – returning the list of students Lname = ‘Stark’
- In SQL – select * from Student where Lname = ‘Stark’

Project Operation (∏)
Use – Fetching on specific columns from a table
Notation – ∏ A1,A2,An(r)
Breakdown –
∏represents Project predicaterfor relationA1, A2, A3for selection from columns for projection
Example 1
- Query
σLname = 'Stark' (Student)σ(select predicate)r(relation) – Employeep(proposition logic) – Lname = ‘Stark’- Result – returning the list of students Lname = ‘Stark’
- In SQL – select * from Student where Lname = ‘Stark’
| ID | Fname | Lname | Age |
|---|---|---|---|
| 1 | Jon | Stark | 25 |
| 2 | Arya | Stark | 28 |
| 3 | Bran | Stark | 26 |
| 4 | Sansa | Stark | 27 |
Union Operation (∪)
Union Operation performs as expected, it essentially finds the union of the tables included in the union i.e finds only the unique rows/tuples from multiple tables, removing the duplications.
Use – Fetching union rows (tuples), i.e unique rows (tuples) from multiple tables removing the duplications
Notation – A(∪)B
Breakdown –
(∪)represents Union Operation- A and B are the tables
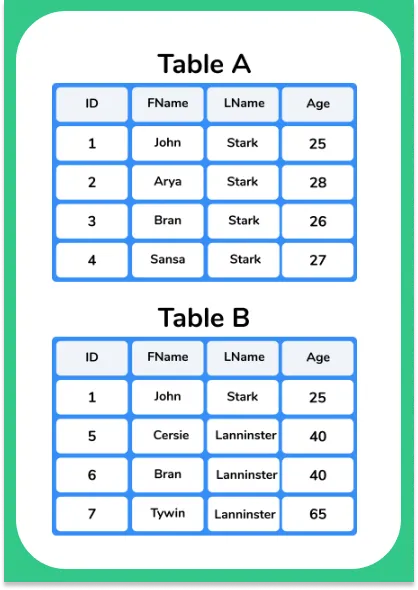
- Query
A(∪)B(∪)(Union Operation)A and BTable- In SQL – SELECT * FROM A UNION SELECT * FROM B;
Resultant
| 1 | Jon | Stark | 25 |
Resultant
Table A
| ID | FNAME | LNAME | AGE |
|---|---|---|---|
| 1 | John | Stark | 25 |
| 2 | Arya | Stark | 28 |
| 3 | Bran | Stark | 26 |
| 4 | Sansa | Stark | 27 |
| 5 | Cersie | Lannister | 40 |
| 6 | Jamie | Lannister | 40 |
| 7 | Tywin | Lannister | 65 |
Intersection Operation (∩)
Intersection operation works simply by helping to find the rows (tuples) that are common i.e. exists in both (all) the tables involved in the intersection operation.
Use – Fetching union rows (tuples), i.e common rows (tuples) from multiple tables and only the rows that exist in both (all) tables involved in the operation.
Notation – A(∩)B
Breakdown –
(∩)represents Intersection Operation- A and B are the tables
Table A
| ID | Fname | Lname | Age |
|---|---|---|---|
| 1 | Jon | Stark | 25 |
| 2 | Arya | Stark | 28 |
| 3 | Bran | Stark | 26 |
| 4 | Sansa | Stark | 27 |
Table B
| ID | Fname | Lname | Age |
|---|---|---|---|
| 1 | Jon | Stark | 25 |
| 5 | Cersie | Lannister | 40 |
| 6 | Jamie | Lannister | 40 |
| 7 | Tywin | Lannister | 65 |
- Query
A(∩)B -
A and BTables(∩)(Intersection Operation)- In SQL – SELECT * FROM A INTERSECT SELECT * FROM B;
Resultant
| ID | Fname | Lname | Age |
| 1 | Jon | Stark | 25 |
∏ player (Cricket) ∪ ∏ player (Football)The following gives the result for selecting the people who either play only cricket or only play football or play both of them.
Set Difference (−)
Use – Fetching rows from which are present in relation but not the other one. Example players who play cricket but don’t play football.
Notation – A - B
Breakdown –
-represents Set Difference Operation- A and B are the tables (relations)
Table Plays Cricket
| ID | Fname |
|---|---|
| 1 | Jon |
| 2 | Arya |
| 3 | Bran |
| 4 | Sansa |
Table Football
| ID | Fname |
|---|---|
| 1 | Jon |
| 2 | Arya |
| 5 | Cersi |
| 6 | Jamie |
- Query
A - B -
A and BTables A: Plays Cricket B: Plays Football-(Intersection Operation)- In SQL – SELECT * FROM A INTERSECT SELECT * FROM B;
Resultant A - B
| ID | Fname |
|---|---|
| 3 | Bran |
| 4 | Sansa |
Resultant B - A
| ID | Fname |
|---|---|
| 5 | Cersie |
| 6 | Jamie |
Cartesian Product (Χ)
Use – Merging columns from two different relations, i.e. combining them together. It is mostly not a suitable and meaningful data representation if we just calculate the cartesian product alone. To get meaningful data we must follow the same by subsequent operations. We will understand more about this in detail.
Notation – A X B
Breakdown –
Xrepresents Cartesian Product- A and B are the tables (relations)
| ID | Fname | Country |
|---|---|---|
| 3 | Bran | UK |
| 4 | Sansa | UK |
| 5 | Jon | India |
| ID | Fname | Country |
|---|---|---|
| 5 | Cersie | India |
| 6 | Jamie | Australia |
| 5 | Samwell | India |
Imaging that we have list of all Facebook and Twitter users and we want to find out the unique list of people from both of them who live in India.
σFname = 'Country'(Facebook Χ Twitter)
Result
| Fname |
|---|
| Jon |
| Samwell |
Rename Operation (ρ)
Use – When we find the result of a some relational operation they are just displayed !. However, we may want to store them in a new relation with a name that we can further use. For the same we use rename operation.
Don’t get confused with the name, the name might give idea that it is done to rename an existing table. However, this is used to store results of relation in a new named table.
Notation – ρx (E)
Breakdown –
ρi.e. rho represents rename operation.xis the new name of the resultant table,- E is the expression used for result.
Use – ρ users (E =A (∩) B)
The results of expression will be stored in new table names as users.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

 0
0



Login/Signup to comment