Minimum Cost Path
Minimum Cost Path
In the Minimum Cost Path problem, we are given a matrix and we have to return the minimum cost from starting point to the destination. In this article, we will provide C++ Solution with an explanation of the problem.

Minimum Cost Path Problem Description
We are given a n*m matrix. Each cell of the matrix has a cost associated to it. We have to return the minimum cost of reaching the destination (n-1,m-1) from the staring cell (0,0).
From any cell we can,
- Move 1 cell right.
- Move 1 cell down.
- Move 1 cell down diagonally.
Input:
- First line contains 2 integers n & m – The dimensions of matrix.
- Next n lines contain m integers each specifying the cost associated with each cell.
Output:
Cost of Minimum Possible Path.
Minimum Cost Path Problem Solution Explanation
Solution (Top Down):
To build a top-down solution we must follow the following steps –
- Break Down the Problem – Let’s suppose we have a function – F(i,j) = Minimum cost of path from (0,0) to(i,j).
For finding F(i,j) we require the cost of (we will take a minimum of all these options)-
F(i-1,j) ie one cell up
F(i,j-1) ie one cell left
F(i-1,j-1) ie one cell upwards but diagonally.
Thus, F(i,j) = cost(i,j) + min({F(i-1,j-1), F(i-1,j),F(i,j-1)})
- Find the base case – The base case is the solution to the smallest known problem. Here F(0,0) ie cost of (0,0) to (0,0) is cost(0,0). Also, we need to keep a check on whether we are inside the grid or not. If we move outside we return a very large value to penalize the result.
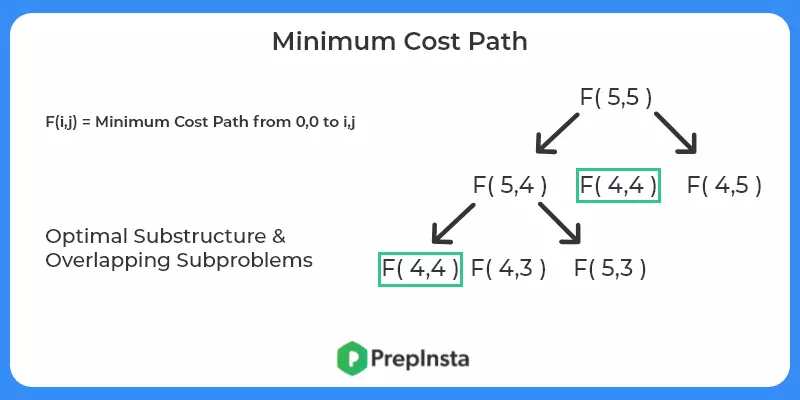
- Check for optimal substructure and overlapping subproblems – It is easy to see that the problem can be broken down into smaller problems. The optimal substructure and overlapping subproblems properties can be visualized below.
Code
Output
3 3
1 2 3
4 5 6
7 8 9
15
Bottom up Solution
Here we create a dp table and where dp[i][j] = minimum cost of path from (0,0) to (i,j).
Now we just have to use same transitions as above. Refer to code for more detail.
Code
Output
3 3
1 2 3
4 5 6
7 8 9
15



Login/Signup to comment