Infix to Postfix in C using Stacks

Infix to Postfix
Any operation can be expressed in Infix, postfix and prefix, we shall see how to convert infix to prefix operation via manual calculation and via code. Lets have a look at Infix to postfix conversion using stack in C
Infix to Postfix in C
- Infix – Any operation of format
a op bformat examplea + bis called an infix operation - Postfix – An operation or expression can also be written in the format of
a b opi.e.a b +which is similar to writinga + bin infix. All we are doing is shifting operator to the right of operands
Why we need postfix operator?
For a compiler, it is easier to read postfix or prefix operation. As a compiler either reads from right to left or left to right. Let us understand this with the help of an example –Imagine the following - a + b * c + d
- Let us assume compiler starts reading from right to left
- It reads
c + dthe operation first and it would be efficient if it could’ve implemented it, but, it can’t as next operation isc * bwhich has higher precedence and must be implemented first. - Thus, if the compiler reads a notation in which, it can keep on implementing operations as soon as it sees them right!
The corresponding Postfix would be: abc*+d+
Steps to convert
- Any infix
op1 oper op2can be written asop1 op2 oper- Where op1 = Operand 1
- op2 = Operand2
- oper = Operation
- Example
a + bcan be written asab+in postfix
Problem
- Infix:
a + b * c + dcan be written asa + (b * c) + d - Now, for all + – / * associativity is left to right we will write it as
(a + (b * c)) + dand thus further((a + (b * c)) + d)- Solving and converting innermost bracket to postfix
- Step 1 –
((a + bc*)+ d) - Step 2 – Consider
bc*as separate operandxthe innermost bracket now looks like((a + x)+ d)- Applying postfix it looks like –
(ax+ + d)replacing x here(abc*+ + d)
- Applying postfix it looks like –
- Step 3 – Considering
abc*+as separate operand z, the final bracket looks like –(z + d)the result would bezd+- replacing z value =
abc*+d+
- replacing z value =
Alert
The above may give wrong results sometimes, which is why its always safer to use below algorithm for both coding and manual calculation -Also note below algorithm is given wrong on Geeks4Geek website, only refer from here.(As most codes are made by interns and PrepInsta pages are made by Ph.D Teachers)
Algorithm
- First Start scanning the expression from left to right
- If the scanned character is an operand, output it, i.e. print it
- Else
- If the precedence of the scanned operator is higher than the precedence of the operator in the stack(or stack is empty or has'(‘), then push operator in the stack
- Else, Pop all the operators, that have greater or equal precedence than the scanned operator. Once you pop them push this scanned operator. (If we see a parenthesis while popping then stop and push scanned operator in the stack)
- If the scanned character is an ‘(‘, push it to the stack.
- If the scanned character is an ‘)’, pop the stack and output it until a ‘(‘ is encountered, and discard both the parenthesis.
- Now, we should repeat the steps 2 – 6 until the whole infix i.e. whole characters are scanned.
- Print output
- Do the pop and output (print) until stack is not empty
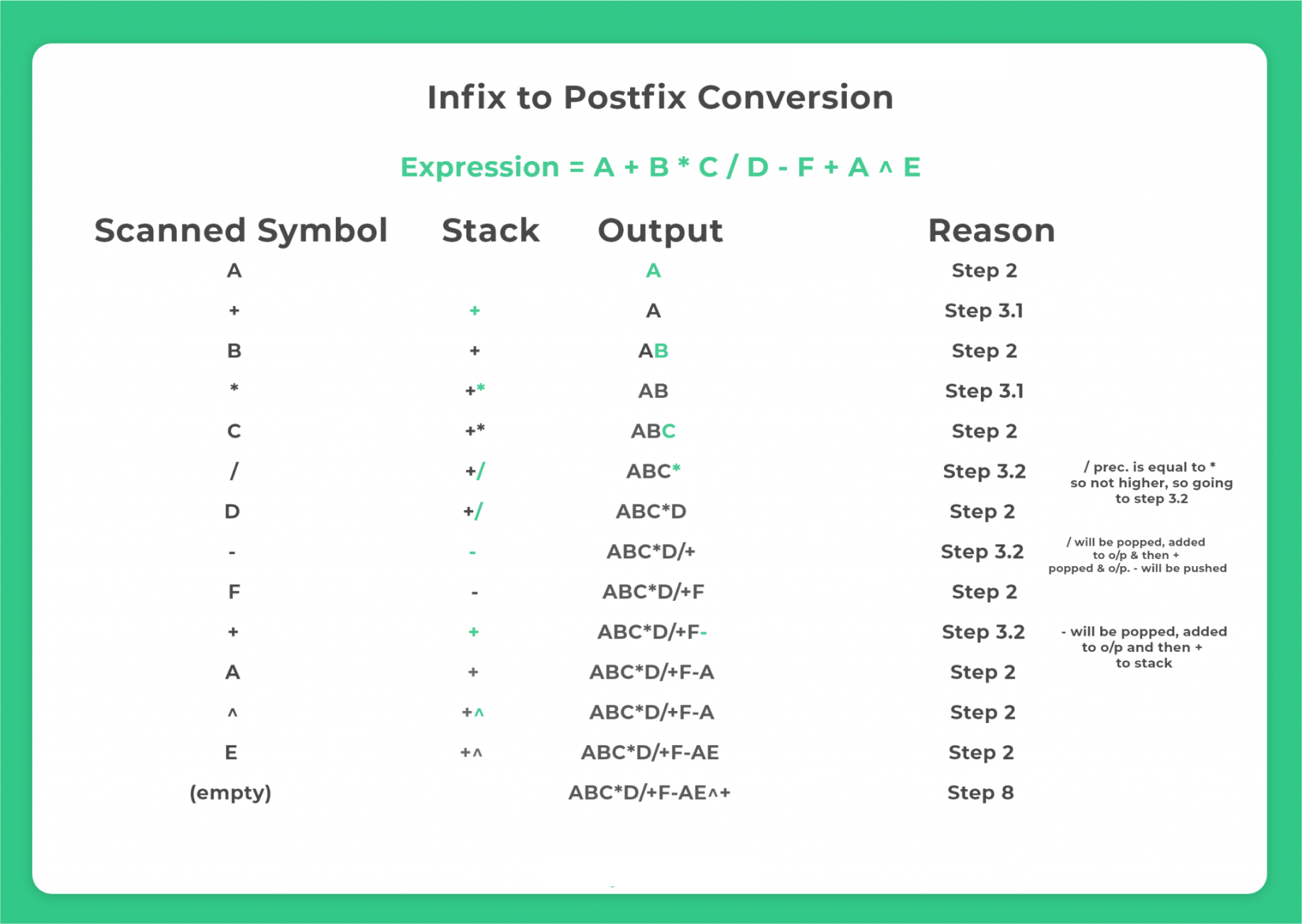
Program for Infix to Postfix in C
We will discuss two methods –
- Method 1: Using array-based stack approach
- Method 2: Using struct based stack approach
Method 1
Method 2
Method 1
This method uses Array based Stack.
Run
// C Program for Infix to Postfix conversion
// Array based stack implimentation
#include<limits.h>
#include<stdio.h>
#include<stdlib.h>
#define MAX 20
char stk[20];
int top = -1;
int isEmpty ()
{
return top == -1;
}
int isFull ()
{
return top == MAX - 1;
}
char peek ()
{
return stk[top];
}
char pop ()
{
if (isEmpty ())
return -1;
char ch = stk[top];
top--;
return (ch);
}
void push (char oper)
{
if (isFull ())
printf ("Stack Full!!!!");
else
{
top++;
stk[top] = oper;
}
}
// A utility function to check if the given character is operand
int checkIfOperand (char ch)
{
return (ch >= 'a' && ch <= 'z') || (ch >= 'A' && ch <= 'Z');
}
// Fucntion to compare precedence
// If we return larger value means higher precedence
int precedence (char ch)
{
switch (ch)
{
case '+':
case '-':
return 1;
case '*':
case '/':
return 2;
case '^':
return 3;
}
return -1;
}
// The driver function for infix to postfix conversion
int covertInfixToPostfix (char *expression)
{
int i, j;
for (i = 0, j = -1; expression[i]; ++i)
{
// Here we are checking is the character we scanned is operand or not
// and this adding to to output
if (checkIfOperand (expression[i]))
expression[++j] = expression[i];
// Here, if we scan character ')', we need push it to the stack.
else if (expression[i] == '(')
push (expression[i]);
/*Here, if we scan character is an ')',
we need to pop and print from the stack
do this until an '(' is encountered in the stack. */
else if (expression[i] == ')')
{
while (!isEmpty () && peek () != '(')
expression[++j] = pop ();
if (!isEmpty () && peek () != '(')
return -1; // invalid expression
else
pop ();
}
else // if an opertor
{
while (!isEmpty ()
&& precedence (expression[i]) <= precedence (peek ()))
expression[++j] = pop ();
push (expression[i]);
}
}
// Once all inital expression characters are traversed
// adding all left elements from stack to exp
while (!isEmpty ())
expression[++j] = pop ();
expression[++j] = '\0';
printf ("%s", expression);
}
int main ()
{
char expression[] = "((a+(b*c))-d)";
covertInfixToPostfix (expression);
return 0;
}
Method 2
This method uses struct based implementation of stack
Run
// This uses struct based stack implimentation of Stack
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<limits.h>
// A structure to represent a stack
struct Stack
{
int top;
int maxSize;
int *array;
};
struct Stack *create (int max)
{
struct Stack *stack = (struct Stack *) malloc (sizeof (struct Stack));
stack->maxSize = max;
stack->top = -1;
stack->array = (int *) malloc (stack->maxSize * sizeof (int));
return stack;
}
// Checking with this function is stack is full or not
// Will return true is stack is full else false
//Stack is full when top is equal to the last index
int isFull (struct Stack *stack)
{
if (stack->top == stack->maxSize - 1)
{
printf ("Will not be able to push maxSize reached\n");
}
// Since array starts from 0, and maxSize starts from 1
return stack->top == stack->maxSize - 1;
}
// By definition the Stack is empty when top is equal to -1
// Will return true if top is -1
int isEmpty (struct Stack *stack)
{
return stack->top == -1;
}
// Push function here, inserts value in stack and increments stack top by 1
void push (struct Stack *stack, int item)
{
if (isFull (stack))
return;
stack->array[++stack->top] = item;
}
// Function to remove an item from stack. It decreases top by 1
int pop (struct Stack *stack)
{
if (isEmpty (stack))
return INT_MIN;
return stack->array[stack->top--];
}
// Function to return the top from stack without removing it
int peek (struct Stack *stack)
{
if (isEmpty (stack))
return INT_MIN;
return stack->array[stack->top];
}
// A utility function to check if the given character is operand
int checkIfOperand (char ch)
{
return (ch >= 'a' && ch <= 'z') || (ch >= 'A' && ch <= 'Z');
}
// Fucntion to compare precedence
// If we return larger value means higher precedence
int precedence (char ch)
{
switch (ch)
{
case '+':
case '-':
return 1;
case '*':
case '/':
return 2;
case '^':
return 3;
}
return -1;
}
// The driver function for infix to postfix conversion
int covertInfixToPostfix (char *expression)
{
int i, j;
// Stack size should be equal to expression size for safety
struct Stack *stack = create (strlen (expression));
if (!stack) // just checking is stack was created or not
return -1;
for (i = 0, j = -1; expression[i]; ++i)
{
// Here we are checking is the character we scanned is operand or not
// and this adding to to output.
if (checkIfOperand (expression[i]))
expression[++j] = expression[i];
else if (expression[i] == '(')
push (stack, expression[i]);
else if (expression[i] == ')')
{
while (!isEmpty (stack) && peek (stack) != '(')
expression[++j] = pop (stack);
if (!isEmpty (stack) && peek (stack) != '(')
return -1; // invalid expression
else
pop (stack);
}
else // if an opertor
{
while (!isEmpty (stack)
&& precedence (expression[i]) <= precedence (peek (stack)))
expression[++j] = pop (stack);
push (stack, expression[i]);
}
}
// Once all inital expression characters are traversed
// adding all left elements from stack to exp
while (!isEmpty (stack))
expression[++j] = pop (stack);
expression[++j] = '\0';
printf ("%s", expression);
}
int main ()
{
char expression[] = "((a+(b*c))-d)";
covertInfixToPostfix (expression);
return 0;
}
Output
abc*+d-
Handling all the cases
In the above program, we assumed that expression will only contain alphabets as operands and ‘(‘ or ‘)’ as brackets.
The below program will handle the cases
- Operands: alphabets or digits
- Example – a-z or A-Z or 0 – 9
- Brackets: { } or [ ] or ( )
Code for this Program
Method 1
Method 2
Method 1
This method uses array based stack approach.
Run
// C Program for Infix to Postfix conversion
// Array based stack implementation
#include<stdlib.h>
#include<stdio.h>
#include<limits.h>
#define MAX 20
char stk[20];
int top = -1;
int isEmpty ()
{
return top == -1;
}
int isFull ()
{
return top == MAX - 1;
}
char peek ()
{
return stk[top];
}
char pop ()
{
if (isEmpty ())
return 0;
char ch = stk[top];
top--;
return (ch);
}
void push (char oper)
{
if (isFull ())
printf ("Stack Full!!!!");
else
{
top++;
stk[top] = oper;
}
}
// A utility function to check if the given character is operand
int checkIfOperand (char ch)
{
return (ch >= 'a' && ch <= 'z') || (ch >= 'A' && ch <= 'Z') || (ch >= '0'
&& ch <=
'9');
}
// Fucntion to compare precedence
// If we return larger value means higher precedence
int precedence (char ch)
{
switch (ch)
{
case '+':
case '-':
return 1;
case '*':
case '/':
return 2;
case '^':
return 3;
}
return -1;
}
// The driver function for infix to postfix conversion
int covertInfixToPostfix (char *expr)
{
int i, j;
for (i = 0, j = -1; expr[i]; ++i)
{
if (checkIfOperand (expr[i]))
expr[++j] = expr[i];
else if (expr[i] == '(' || expr[i] == '[' || expr[i] == '{')
push (expr[i]);
else if (expr[i] == ')' || expr[i] == '}' || expr[i] == ']')
{
if (expr[i] == ')')
{ // keep popping & adding to expression until opening pair found
while (!isEmpty () && peek () != '(')
expr[++j] = pop ();
// pops '('
pop ();
}
if (expr[i] == ']')
{ // keep popping & adding to expression until opening pair found
while (!isEmpty () && peek () != '[')
expr[++j] = pop ();
// pops '['
pop ();
}
if (expr[i] == '}')
{ // keep popping & adding to expression until opening pair found
while (!isEmpty () && peek () != '{')
expr[++j] = pop ();
// pops '}'
pop ();
}
}
else // if an opertor
{
while (!isEmpty () && precedence (expr[i]) <= precedence (peek ()))
expr[++j] = pop ();
push (expr[i]);
}
}
// Once all inital expression characters are traversed
// adding all left elements from stack to exp
while (!isEmpty ())
expr[++j] = pop ();
expr[++j] = '\0';
printf ("%s", expr);
}
int main ()
{
char expression[] = "{[a(3*5)]-d}";
covertInfixToPostfix (expression);
return 0;
}
Method 2
Struct based stack approach
Run
// This uses struct based stack implimentation of Stack
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<limits.h>
// A structure to represent a stack
struct Stack
{
int top;
int maxSize;
// we are storing string in integer array, this will not give error
// as values will be stored in ASCII and returned in ASCII thus, returned as string again
int *array;
};
struct Stack *create (int max)
{
struct Stack *stack = (struct Stack *) malloc (sizeof (struct Stack));
stack->maxSize = max;
stack->top = -1;
stack->array = (int *) malloc (stack->maxSize * sizeof (int));
return stack;
}
// Checking with this function is stack is full or not
// Will return true is stack is full else false
//Stack is full when top is equal to the last index
int isFull (struct Stack *stack)
{
if (stack->top == stack->maxSize - 1)
{
printf ("Will not be able to push maxSize reached\n");
}
// Since array starts from 0, and maxSize starts from 1
return stack->top == stack->maxSize - 1;
}
// By definition the Stack is empty when top is equal to -1
// Will return true if top is -1
int isEmpty (struct Stack *stack)
{
return stack->top == -1;
}
// Push function here, inserts value in stack and increments stack top by 1
void push (struct Stack *stack, int item)
{
if (isFull (stack))
return;
stack->array[++stack->top] = item;
}
// Function to remove an item from stack. It decreases top by 1
int pop (struct Stack *stack)
{
if (isEmpty (stack))
return INT_MIN;
return stack->array[stack->top--];
}
// Function to return the top from stack without removing it
int peek (struct Stack *stack)
{
if (isEmpty (stack))
return INT_MIN;
return stack->array[stack->top];
}
// A utility function to check if the given character is operand
int checkIfOperand (char ch)
{
return (ch >= 'a' && ch <= 'z') || (ch >= 'A' && ch <= 'Z') || (ch >= '0'
&& ch <=
'9');
}
// Fucntion to compare precedence
// If we return larger value means higher precedence
int precedence (char ch)
{
switch (ch)
{
case '+':
case '-':
return 1;
case '*':
case '/':
return 2;
case '^':
return 3;
}
return -1;
}
// The driver function for infix to postfix conversion
int covertInfixToPostfix (char *expr)
{
int i, j;
// Stack size should be equal to expression size for safety
struct Stack *stack = create (strlen (expr));
if (!stack) // just checking is stack was created or not
return -1;
for (i = 0, j = -1; expr[i]; ++i)
{
// Here we are checking is the character we scanned is operand or not
// and this adding to to output.
if (checkIfOperand (expr[i]))
expr[++j] = expr[i];
else if (expr[i] == '(' || expr[i] == '[' || expr[i] == '{')
push (stack, expr[i]);
else if (expr[i] == ')' || expr[i] == '}' || expr[i] == ']')
{
if (expr[i] == ')')
{
while (!isEmpty (stack) && peek (stack) != '(')
expr[++j] = pop (stack);
// pops '('
pop (stack);
}
if (expr[i] == ']')
{
while (!isEmpty (stack) && peek (stack) != '[')
expr[++j] = pop (stack);
// pops '['
pop (stack);
}
if (expr[i] == '}')
{
while (!isEmpty (stack) && peek (stack) != '{')
expr[++j] = pop (stack);
// pops '}'
pop (stack);
}
}
else // if an opertor
{
while (!isEmpty (stack)
&& precedence (expr[i]) <= precedence (peek (stack)))
expr[++j] = pop (stack);
push (stack, expr[i]);
}
}
// Once all inital expression characters are traversed
// adding all left elements from stack to exp
while (!isEmpty (stack))
expr[++j] = pop (stack);
expr[++j] = '\0';
printf ("%s", expr);
}
int main ()
{
char expression[] = "{[a(3*5)]-d}";
covertInfixToPostfix (expression);
return 0;
}
Output
a35*d-
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Stacks
- Introduction to Stack in Data Structure
- Operations on a Stack
- Stack: Infix, Prefix and Postfix conversions
- Stack Representation in – C | C++ | Java
- Representation of a Stack as an Array. – C | C++ | Java
- Representation of a Stack as a Linked List. – C | C++ | Java
- Infix to Postfix Conversion – C | C++ | Java
- Infix to prefix conversion in – C | C++ | Java
- Postfix to Prefix Conversion in – C | C++ | Java
Queues
- Queues in Data Structures (Introduction)
- Queues Program in C and implementation
- Implementation of Queues using Arrays | C Program
- Types of Queues in Data Structure
- Application of Queue Data Structure
- Insertion in Queues Program (Enqueuing) – C | C++ | Java
- Deletion (Removal) in Queues Program(Dequeuing) – C | C++ | Java
- Reverse a Queue – C | C++ | Java
- Queues using Linked Lists – C | C++ | Java
- Implement Queue using Stack – C | C++ | Java
- Implement Queue using two Stacks – C | C++ | Java
Circular Queues
- Circular queue in Data Structure
- Applications of Circular Queues
- Circular queue in – C | C++ | Java
- Circular queue using Array – C | C++ | Java
- Circular Queue using Linked Lists – C | C++ | Java
Priority Queue
Stacks
- Introduction to Stack in Data Structure
Click Here - Operations on a Stack
Click Here - Stack: Infix, Prefix and Postfix conversions
Click Here - Stack Representation in –
C | C++ | Java - Representation of a Stack as an Array. –
C | C++ | Java - Representation of a Stack as a Linked List. –
C | C++ | Java - Infix to Postfix Conversion –
C | C++ | Java - Infix to prefix conversion in –
C | C++ | Java - Postfix to Prefix Conversion in –
C | C++ | Java
Queues
- Queues in Data Structures (Introduction)
Click Here - Queues Program in C and implementation
Click Here - Implementation of Queues using Arrays | C Program
Click Here - Types of Queues in Data Structure
Click Here - Application of Queue Data Structure
Click Here - Insertion in Queues Program (Enqueuing) –
C | C++ | Java - Deletion (Removal) in Queues Program(Dequeuing) –
C | C++ | Java - Reverse a Queue –
C | C++ | Java - Queues using Linked Lists –
C | C++ | Java - Implement Queue using Stack –
C | C++ | Java - Implement Queue using two Stacks –
C | C++ | Java
Circular Queues
- Circular queue in Data Structure
Click Here - Applications of Circular Queues
Click Here - Circular queue in –
C | C++ | Java - Circular queue using Array –
C | C++ | Java - Circular Queue using Linked Lists –
C | C++ | Java






Login/Signup to comment