Representation of a Stack using a Linked List
Representation of Stack using a Linked List in C++
One of the basic linear user defined data structure that is also very useful to solve problems and implement tons of Graph theory algorithms is Stack. It follows the last in first out model and cann be implemented using LinkedList if you want to get its size changing dynamically. This is anarticle on the Representation of a Stack using a Linked List.

What is Stack?
Stack is a data structure where you can add any kind of and store then in a LIFO (last in first out) manner.
- If you want to know about The given stack Data structure in a C++ STL, here it goes: Stack in C++ STL
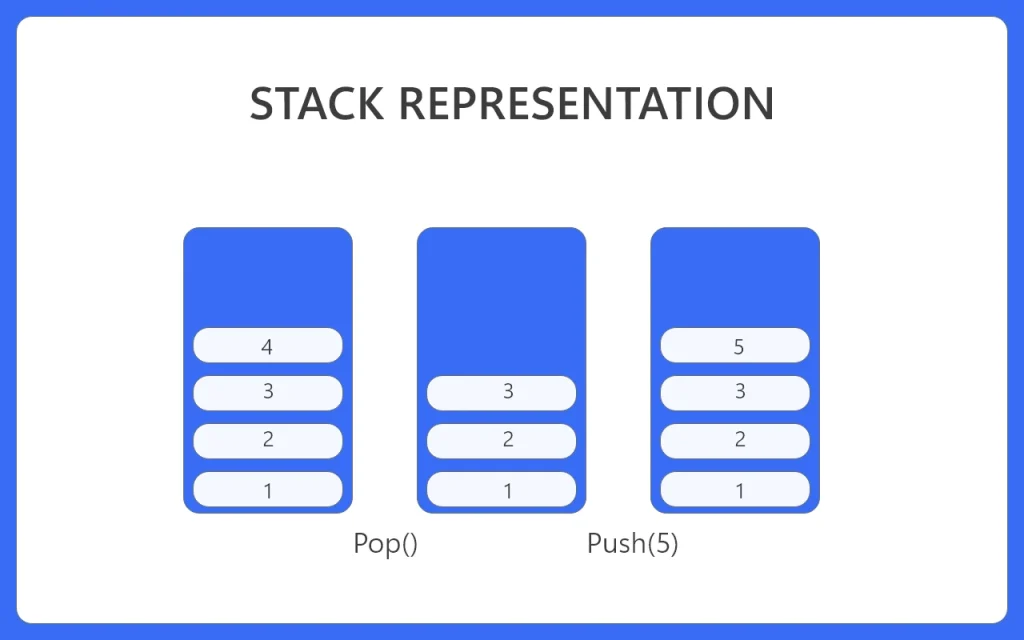

The Algorithm Goes here:
So here goes the algorithm about How to use a linked list to implement a stack. It is one of the easiest algorithms, if you know what a linked list is. Here we used the inbuilt STL List (List in C++ STL) as a linked list inside a ‘Stack’ named class, otherwise you can make a class or structure with pointers to make a Linked List.
- Firstly, This is a LinkedList, where only the last element is visible. So you have only one place open to change in the list, that is the topmost node of the list.
- So if you want to push values, you have to push them at the back. Only if the list is empty, you can push the first value in the first node.
- If you want to pop values, only the topmost or the last pushed place is accessible. If the list is empty, no values can be popped, otherwise, the momentary topmost value is to be popped.
- That is how you can achieve the model of Last in First Out.
- So Here a class is made with a list member. Then values are added only at the back, same goes for the popping.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
The code to implement this:
The code for representing a stack using a linked list demonstrates how dynamic memory allocation allows flexible stack operations without worrying about size limits. Each node holds data and a pointer to the next, making push and pop operations efficient and adaptable.
- It efficiently utilizes memory by allocating nodes dynamically during runtime.
- The linked list implementation avoids stack overflow issues seen in array-based stacks.
Run
#include<bits/stdc++.h>
using namespace std;
class Stack
{
public:
list < int >L;
void Push (int i)
{
cout << "Pushing the element : " << (i) << endl;
L.push_back (i);
}
int pop ()
{
if (L.empty ())
{
cout << "The Stack is empty" << endl;
}
int a = L.back ();
L.pop_back ();
cout << "Popping the element : " << a << endl;
return a;
}
void Show ()
{
cout << "The present Stack is:" << endl;
for (auto i:L)
cout << i << " ";
cout << endl;
}
};
int main ()
{
Stack s;
s.Push (5);
s.Push (2);
s.Push (11);
s.Show ();
s.pop ();
s.Push (12);
s.Show ();
}
Output:
Pushing the element : 5 Pushing the element : 2 Pushing the element : 11 The present Stack is: 5 2 11 Popping the element : 11 Pushing the element : 12 The present Stack is: 5 2 12
Explanation:
- The code begins by defining a Stack class that utilizes the STL list to store elements, ensuring efficient insertion and deletion.
- Inside the Push() method, each new element is appended at the end of the list using push_back(), and the pushed value is displayed.
- When pop() is called, it retrieves and removes the last element using pop_back(), also checking if the stack is empty before performing the operation.
- To view the contents, the Show() function iterates through the list and prints all current elements in the stack.
- Finally, in the main() function, various push and pop operations are executed to demonstrate the LIFO (Last In First Out) nature of the stack.
Time and Space Complexity:
| Operation | Time Complexity | Space Complexity |
|---|---|---|
| Push Operation | O(1) | O(1) |
| Pop Operation | O(1) | O(1) |
| Show / Display Stack | O(n) | O(1) |
| Overall Space Used by Stack | — | O(n) |
To wrap it up:
The concept of representing a stack using a linked list in C++ offers better flexibility compared to array implementation. It allows efficient push and pop operations without worrying about overflow, as memory is allocated dynamically according to the number of elements.
Understanding this approach helps strengthen core data structure knowledge and is extremely useful for solving interview-level coding problems. Practising such programs on PrepInsta can enhance your grasp of linked list operations and improve your coding efficiency.
FAQs
A linked list is preferred because it provides dynamic memory allocation, eliminating the need to define a fixed stack size and preventing overflow issues.
Both push and pop operations have a time complexity of O(1), as they involve inserting or deleting a node at the beginning of the list.
Yes, a stack can be implemented using a doubly linked list, but it increases memory usage without offering significant benefits over a singly linked list.
Memory is allocated dynamically for each new node and freed when an element is popped, ensuring optimal memory utilization.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Stacks
- Introduction to Stack in Data Structure
Click Here - Operations on a Stack
Click Here - Stack: Infix, Prefix and Postfix conversions
Click Here - Stack Representation in –
C | C++ | Java - Representation of a Stack as an Array. –
C | C++ | Java - Representation of a Stack as a Linked List. –
C | C++ | Java - Infix to Postfix Conversion –
C | C++ | Java - Infix to prefix conversion in –
C | C++ | Java - Postfix to Prefix Conversion in –
C | C++ | Java
Queues
- Queues in Data Structures (Introduction)
Click Here - Queues Program in C and implementation
Click Here - Implementation of Queues using Arrays | C Program
Click Here - Types of Queues in Data Structure
Click Here - Application of Queue Data Structure
Click Here - Insertion in Queues Program (Enqueuing) –
C | C++ | Java - Deletion (Removal) in Queues Program(Dequeuing) –
C | C++ | Java - Reverse a Queue –
C | C++ | Java - Queues using Linked Lists –
C | C++ | Java - Implement Queue using Stack –
C | C++ | Java - Implement Queue using two Stacks –
C | C++ | Java
Circular Queues
- Circular queue in Data Structure
Click Here - Applications of Circular Queues
Click Here - Circular queue in –
C | C++ | Java - Circular queue using Array –
C | C++ | Java - Circular Queue using Linked Lists –
C | C++ | Java
Priority Queue
Stacks
- Introduction to Stack in Data Structure
- Operations on a Stack
- Stack: Infix, Prefix and Postfix conversions
- Stack Representation in – C | C++ | Java
- Representation of a Stack as an Array. – C | C++ | Java
- Representation of a Stack as a Linked List. – C | C++ | Java
- Infix to Postfix Conversion – C | C++ | Java
- Infix to prefix conversion in – C | C++ | Java
- Postfix to Prefix Conversion in – C | C++ | Java
Queues
- Queues in Data Structures (Introduction)
- Queues Program in C and implementation
- Implementation of Queues using Arrays | C Program
- Types of Queues in Data Structure
- Application of Queue Data Structure
- Insertion in Queues Program (Enqueuing) – C | C++ | Java
- Deletion (Removal) in Queues Program(Dequeuing) – C | C++ | Java
- Reverse a Queue – C | C++ | Java
- Queues using Linked Lists – C | C++ | Java
- Implement Queue using Stack – C | C++ | Java
- Implement Queue using two Stacks – C | C++ | Java
Circular Queues
- Circular queue in Data Structure
- Applications of Circular Queues
- Circular queue in – C | C++ | Java
- Circular queue using Array – C | C++ | Java
- Circular Queue using Linked Lists – C | C++ | Java
Priority Queue
FAQs - Stack using a Linked List
In a linked list-based stack, memory is allocated dynamically during runtime using pointers (e.g., new in C++ or malloc in C). This means the stack can grow as long as the system has free memory, reducing the chances of overflow. In contrast, an array-based stack has a fixed size, so it can overflow even if the system has free memory. However, dynamic allocation comes at the cost of increased overhead and slightly slower performance due to pointer management.
Both implementations provide O(1) time complexity for push() and pop() operations. However, array-based stacks may occasionally face O(n) complexity during dynamic resizing (in languages like Java with ArrayList). Linked list stacks always maintain O(1) time, but at the cost of extra memory for storing pointers and less cache locality, which can slow down operations in practice.
Linked list-based stacks allocate memory for each node individually, which can lead to memory fragmentation if there are frequent allocations and deallocations. Fragmentation can reduce performance over time due to inefficient memory access and increased overhead in memory management. In contrast, array-based stacks allocate memory in contiguous blocks, improving spatial locality and reducing fragmentation.
Linked list-based stacks involve frequent pointer updates (next and top), which are not atomic operations. In a multithreaded environment, this can lead to race conditions, data corruption, or segmentation faults. To mitigate this, developers must use mutex locks, atomic operations, or implement lock-free data structures using CAS (Compare-And-Swap) operations. Ensuring thread safety adds complexity and may reduce performance due to synchronization overhead.
In garbage-collected languages, unreferenced nodes in a linked list stack are cleaned up automatically. However, frequent node allocation and deallocation can trigger the garbage collector more often, potentially leading to GC pauses and degraded performance. Moreover, if references to nodes are not released properly (e.g., through circular references), memory leaks may still occur. Proper nullification of node references is critical for efficient memory usage.




Login/Signup to comment