Program for Priority Queue Insertion and Deletion in C++
Priority Queue Insertion and Deletion in C++
In this page, we will explore how Priority Queue insertion and deletion work in C++ with clear examples and an easy-to-understand approach. You’ll learn how elements are arranged based on their priority and how the queue ensures that the highest-priority element is always processed first.
We will also walk through an efficient method to insert new elements and remove existing ones, helping you understand the internal working of priority queues in C++ for better implementation in real-world problems.
What is Priority Queue?
A priority is basically an extension of the general queue. A major difference is that dequeuing happens based on the priority of each item in the queue.Types of Priority Queue :
Max Priority Queue – A larger priority value means higher priorityMin Priority Queue – A smaller priority value means lower priority
Operations on Priority Queue
Different operations that can be performed on priority queue are given below,
- enqueue()
- dequeue()
- peek()/top()
Let’s discuss each operations in brief,
enqueue()
- Adding a new item to the Queue Data Structure, in other words Enqueue new item to Queue If Queue is full, then it is said to be in an overflow condition.
- When we require to add an element and its priority to the queue we perform enqueue() operation.
- Enqueue() operation is synonymous of insertion in a data structure Queue.
Time-Complexity of enqueue() operation
The time complexity for inserting an element in the priority queue is O(1)
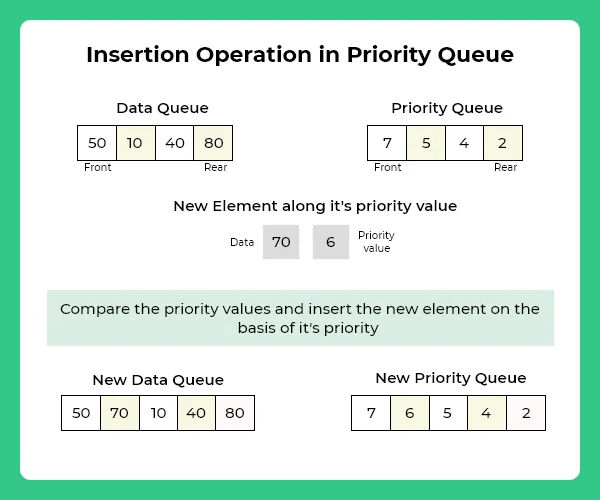
dequeue()
- Delete a item from a Queue, Deletion based on priority, highest priority element deleted first.In other words Dequeue item from Queue If queue is empty then it is said to be in an underflow condition.
- When we require to delete an element and its priority from the queue we perform dequeue() operation.
- dequeue() operation is synonymous of deletion in a data structure Queue.
Time-Complexity of dequeue() operation
The time complexity for deleting an element in the priority queue is O(N)

peek()/top()
This function returns the element with highest priority in the given priority queue.
- Traverse the entire priority queue and find the element with the highest priority and return its index.
- In the case of multiple elements with the same priority, find the element with the highest value having the highest priority.
Time-Complexity of peek() operation
The time complexity for finding the element with highest priority is O(N)
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Code Implementation for Priority Queue Insertion and Deletion
Code implementation for Priority Queue insertion and deletion in C++ focuses on managing elements based on their priority rather than their arrival order. It ensures that the highest priority element is always accessed first, making operations efficient and structured. This approach is widely used in scheduling, optimization, and real time processing.
- Insertion places elements in the queue while maintaining proper priority order for quick access.
- Deletion always removes the element with the highest priority, ensuring reliable and predictable processing.
#include<iostream>
#include<limits.h>
#define MAX 100
using namespace std;
// struct to hold data and priority of any item in priority queue
struct item
{
int data;
int priority;
};
// array of type struct item
// example rather than int array[] we have item array[]
// item is a struct that holds data and priority
item pq[MAX];
// denotes where the last item in priority queue is
// initialized to -1 since no item is in queue
int idx = -1;
bool isEmpty ()
{
return idx == -1;
}
bool isFull ()
{
return idx == MAX - 1;
}
// enqueue just adds item to the end of the priority queue | O(1)
void enqueue (int data, int priority)
{
if (!isFull ())
{
// Increase the index
idx++;
// Insert the element in priority queue
pq[idx].data = data;
pq[idx].priority = priority;
}
}
// returns item with highest priority
// NOTE: Low priority number means higher priority | O(N)
int peek ()
{
int maxPriority = INT_MAX;
int indexPos = -1;
// Linear search for highest priority
for (int i = 0; i <= idx; i++) { // If two items have same priority choose the one with // higher data value if (maxPriority == pq[i].priority && indexPos > -1
&& pq[indexPos].data < pq[i].data) { maxPriority = pq[i].priority; indexPos = i; } // note low priority number means higher priority // ex: Two processes P1 - 1 priority and P2 - 5 priority // P1 will get executed first, thus comes out of ready queue first else if (maxPriority > pq[i].priority)
{
maxPriority = pq[i].priority;
indexPos = i;
}
}
// Return index of the element where
return indexPos;
}
// This removes the element with highest priority
// from the priority queue | O(N)
void dequeue ()
{
if (!isEmpty ())
{
// Get element with highest priority
int indexPos = peek ();
// reduce size of priority queue by first
// shifting all elements one position left
// from index where the highest priority item was found
for (int i = indexPos; i < idx; i++)
{
pq[i] = pq[i + 1];
}
// reduce size of priority queue by 1
idx--;
}
}
void display ()
{
for (int i = 0; i <= idx; i++)
{
cout << "(" << pq[i].data << ", " << pq[i].priority << ")\n";
}
}
// Driver Code
int main ()
{
// To enqueue items as per priority
enqueue (10, 1);
enqueue (20, 3);
enqueue (30, 4);
enqueue (40, 5);
enqueue (1000, 2);
cout << "Before: " << endl;
display ();
// Dequeue the top element
dequeue (); // 10 dequeued
dequeue (); // 1000 dequeued
cout << "\nAfter: " << endl;
display ();
return 0;
}
Output:
Before : (10, 1) (20, 3) (30, 4) (40, 5) (1000, 2) After : (20, 3) (30, 4) (40, 5)
Explanation:
- The code stores each element as a struct containing both data and priority inside a fixed-size array.
- enqueue() simply inserts the new element at the end of the array, so insertion is always O(1).
- peek() performs a linear search to find the item with the highest priority (smallest priority value).
- dequeue() removes that highest-priority item by shifting all elements left from that index, making deletion O(N).
- The queue keeps track of the last index using idx, which makes checking full/empty conditions easy and efficient.
Time and Space Complexity:
| Operation | Time Complexity | Space Complexity |
|---|---|---|
| Enqueue | O(1) | O(1) |
| Peek (Find Highest Priority) | O(N) | O(1) |
| Dequeue | O(N) | O(1) |
| Overall Space Used | — | O(N) |
To Wrap It Up:
The implementation of priority queue insertion and deletion in C++ effectively demonstrates how tasks can be managed based on their importance rather than their order of arrival. By separating data and priority values, the program offers a clear and structured approach to handling prioritized operations.
Overall, the concept is made easy to understand through clean logic and step-by-step execution of enqueue and dequeue functions. This makes the implementation suitable for both learning and applying priority-based processing in real-world scenarios.
FAQs
A priority queue is a special queue where elements are removed based on priority instead of FIFO order. Higher-priority elements always get processed first.
Insertion simply adds the element to the end of the array, making it a constant-time operation. The priority is stored alongside the data for later comparison.
Deletion searches the entire array to find the element with the highest priority. After locating it, the element is removed and the array is adjusted.
Use a priority queue when tasks must be executed based on importance rather than order of arrival. It is ideal for scheduling, simulations, and path-finding algorithms.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Stacks
- Introduction to Stack in Data Structure
Click Here - Operations on a Stack
Click Here - Stack: Infix, Prefix and Postfix conversions
Click Here - Stack Representation in –
C | C++ | Java - Representation of a Stack as an Array. –
C | C++ | Java - Representation of a Stack as a Linked List. –
C | C++ | Java - Infix to Postfix Conversion –
C | C++ | Java - Infix to prefix conversion in –
C | C++ | Java - Postfix to Prefix Conversion in –
C | C++ | Java
Queues
- Queues in Data Structures (Introduction)
Click Here - Queues Program in C and implementation
Click Here - Implementation of Queues using Arrays | C Program
Click Here - Types of Queues in Data Structure
Click Here - Application of Queue Data Structure
Click Here - Insertion in Queues Program (Enqueuing) –
C | C++ | Java - Deletion (Removal) in Queues Program(Dequeuing) –
C | C++ | Java - Reverse a Queue –
C | C++ | Java - Queues using Linked Lists –
C | C++ | Java - Implement Queue using Stack –
C | C++ | Java - Implement Queue using two Stacks –
C | C++ | Java
Circular Queues
- Circular queue in Data Structure
Click Here - Applications of Circular Queues
Click Here - Circular queue in –
C | C++ | Java - Circular queue using Array –
C | C++ | Java - Circular Queue using Linked Lists –
C | C++ | Java
Priority Queue
Stacks
- Introduction to Stack in Data Structure
- Operations on a Stack
- Stack: Infix, Prefix and Postfix conversions
- Stack Representation in – C | C++ | Java
- Representation of a Stack as an Array. – C | C++ | Java
- Representation of a Stack as a Linked List. – C | C++ | Java
- Infix to Postfix Conversion – C | C++ | Java
- Infix to prefix conversion in – C | C++ | Java
- Postfix to Prefix Conversion in – C | C++ | Java
Queues
- Queues in Data Structures (Introduction)
- Queues Program in C and implementation
- Implementation of Queues using Arrays | C Program
- Types of Queues in Data Structure
- Application of Queue Data Structure
- Insertion in Queues Program (Enqueuing) – C | C++ | Java
- Deletion (Removal) in Queues Program(Dequeuing) – C | C++ | Java
- Reverse a Queue – C | C++ | Java
- Queues using Linked Lists – C | C++ | Java
- Implement Queue using Stack – C | C++ | Java
- Implement Queue using two Stacks – C | C++ | Java
Circular Queues
- Circular queue in Data Structure
- Applications of Circular Queues
- Circular queue in – C | C++ | Java
- Circular queue using Array – C | C++ | Java
- Circular Queue using Linked Lists – C | C++ | Java




Login/Signup to comment