Priority Queue implementation using Array in C++

November 18, 2025

Implementation of Priority Queue using Arrays in C++

Priority Queue implementation using Array in C++ is not so complicated operation. We can take two arrays one for priority and second for the data. And maintain the data and there respective priority using the index of array.

There you can learn how we can implement priority queue using array and different methods to implement it.

Priority queue implementation using array in C++

Priority Queue Implementation in C++

Using ordered Array

  • In ordered Array elements store in sorted for it can be in ascending order or descending order.
  • So insertion takes O(n) time complexity. and deletion takes O(1) time complexity.

Using unordered Array

  • In unordered Array elements store in as they insert in Queue there is no sorting.

  • So Insertion takes o(1) time complexity and deletion takes o(n) time complexity.

Steps for Implementing Priority Queue in C++

Insertion

  • Take data and priority from the user.
  • Check if Queue is not full.
  • If f=0 and rear = n-1 then print Queue is full,
  • If f == r ==-1 then increment both with 1 and enqueue data from the rear.
  • Else if there is some elements in array we will compare the priority of entered element with the priority of elements in Queue.
  • When we finds out the position of element which is smaller then entered priority then we insert the entered element before it.

Deletion

  • If front == -1 then print underflow condition.
  • Else print the element from the front.
  • If front == rear then initialize front = rear =-1
  • Else increment front by 1.

Print

  • Traverse a Queue with the help of loop from front to rear and print the data and priority of Queue.
Priority Queue implementation using array in C Programming – 1

Application of Priority Queue

Priority Queue Example

Priority Queue Implementation using Array

Priority Queue using Linked List

Priority Queue Insertion and Deletion

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

C++ Program to Implement Max Priority Queue (using Ordered Array)

A C++ Program to Implement a Max Priority Queue using an Ordered Array stores elements in sorted order so the maximum element is always at the end of the array. This approach makes deletion of the maximum very efficient, as it can be removed in constant time. Although insertion takes linear time, it ensures quick access to the highest-priority element.

Run

#include<iostream>
#define N 20
using namespace std;
int Q[N], Pr[N];
int r = -1, f = -1;
void enqueue (int data, int p)	//Enqueue function to insert data and its priority in queue
{
  int i;
  if ((f == 0) && (r == N - 1))	//Check if Queue is full
    cout << "Queue is full";
  else
    {
      if (f == -1)		//if Queue is empty
	{
	  f = r = 0;
	  Q[r] = data;
	  Pr[r] = p;

	}
      else if (r == N - 1)	//if there there is some elemets in Queue
	{
	  for (i = f; i <= r; i++) { Q[i - f] = Q[i]; Pr[i - f] = Pr[i]; r = r - f; f = 0; for (i = r; i > f; i--)
		{
		  if (p > Pr[i])
		    {
		      Q[i + 1] = Q[i];
		      Pr[i + 1] = Pr[i];
		    }
		  else
		    break;
		  Q[i + 1] = data;
		  Pr[i + 1] = p;
		  r++;
		}
	    }
	}
      else
	{
	  for (i = r; i >= f; i--)
	    {
	      if (p > Pr[i])
		{
		  Q[i + 1] = Q[i];
		  Pr[i + 1] = Pr[i];
		}
	      else
		break;
	    }
	  Q[i + 1] = data;
	  Pr[i + 1] = p;
	  r++;
	}
    }

}

void display ()			//print the data of Queue
{
  int i;
  for (i = f; i <= r; i++)
    {
      cout << "Element =" << Q[i] << " Priority = " << Pr[i] << endl;
    }
}

void dequeue ()			//remove the data from front
{
  if (f == -1)
    {
      cout << "Queue is Empty";
    }
  else
    {
      cout << "deleted Element =" << Q[f] << endl;
      cout << "Its Priority = " << Pr[f] << endl;
      if (f == r)
	f = r = -1;
      else
	f++;
    }
}

int main ()
{
  int opt, n, i, data, p;
  cout << "Enter Your Choice:-" << endl;
  do
    {
      cout <<
	"1 for Insert the Data in Queue\n2 for show the Data in Queue \n3 for Delete the data from the Queue\n0 for Exit"
	<< endl; cin >> opt;
      switch (opt)
	{
	case 1:
	  cout << "Enter the number of data" << endl; cin >> n;
	  cout << "Enter your data and Priority of data" << endl;
	  i = 0;
	  while (i < n) { cin >> data;
	      cin >> p;
	      enqueue (data, p);
	      i++;
	    }
	  break;
	case 2:
	  display ();
	  break;
	case 3:
	  dequeue ();
	  break;
	case 0:
	  break;
	default:
	  cout << "Incorrect Choice" << endl;

	}
    }
  while (opt != 0);
  return 0;
}

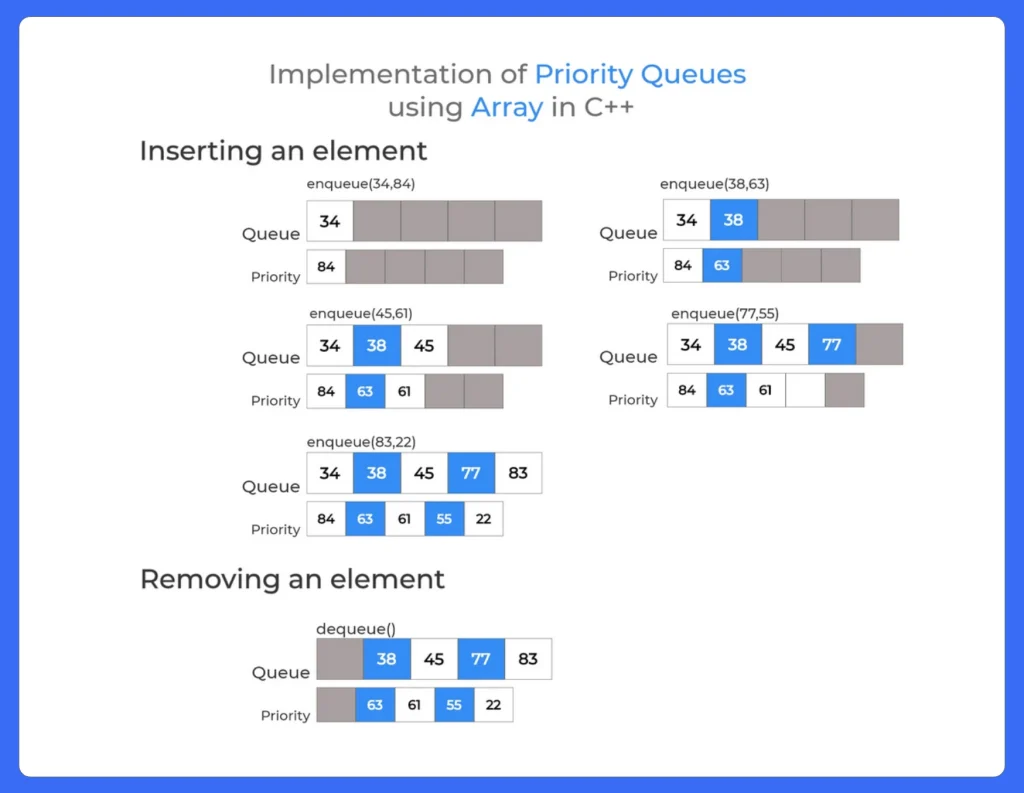
Enter Your Choice:-
1 for Insert the Data in Queue
2 for show the Data in Queue
3 for Delete the data from the Queue
0 for Exit
1

Enter the number of data 5

Enter your data and Priority of data
34 84
38 63
45 61
77 55
83 22

1 for Insert the Data in Queue
2 for show the Data in Queue
3 for Delete the data from the Queue
0 for Exit
3
deleted Element = 34 Its Priority = 84

1 for Insert the Data in Queue
2 for show the Data in Queue
3 for Delete the data from the Queue
0 for Exit
2

Element = 38 Priority = 63
Element = 45 Priority = 61
Element = 77 Priority = 55
Element = 83 Priority = 22

1 for Insert the Data in Queue
2 for show the Data in Queue
3 for Delete the data from the Queue
0 for Exit

Explanation:

  • The code stores elements and their priorities in two arrays and keeps the queue ordered so that higher-priority elements always stay in front.
  • The enqueue function shifts elements to make space for the new value so the correct priority order is maintained.
  • When the rear reaches the end but space exists at the front, the queue elements are compacted toward index 0 to free space.
  • The dequeue function removes the front element in constant time by simply moving the front index forward.
  • Display prints all active elements between the front and rear indices.

Time and Space Complexity:

OperationTime ComplexitySpace Complexity
EnqueueO(N)O(1)
DequeueO(1)O(1)
DisplayO(n)O(1)
Total Memory Used—O(N)

To wrap it up:

The priority queue implementation using arrays provides a simple and clear way to understand how elements are arranged based on their priority. It demonstrates how insertion and deletion operations work and how priority influences which element gets removed first.

Although easy to implement, array-based priority queues can become inefficient for large datasets due to shifting and scanning operations. Still, they serve as a strong foundation for learning before moving to advanced structures like heaps.

FAQs

A priority queue is a data structure where each element has a priority, and the element with the highest priority is removed first. It works similar to a queue but follows priority-based ordering.

Insertion is costly because elements must be placed in sorted order, requiring shifting existing elements. This increases the time complexity as the array grows.

Deletion becomes slow because the entire array must be scanned to find the highest-priority element. This leads to increased time complexity for each delete operation.

The static size and frequent shifting or scanning make arrays inefficient for large data. Dynamic structures like heaps handle growth and operations more efficiently.

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout

Stacks

  • Introduction to Stack in Data Structure
    Click Here
  • Operations on a Stack
    Click Here
  • Stack: Infix, Prefix and Postfix conversions
    Click Here
  • Stack Representation in –
    C | C++ | Java
  • Representation of a Stack as an Array. –
    C | C++ | Java
  • Representation of a Stack as a Linked List. –
    C | C++ | Java
  • Infix to Postfix Conversion –
    C | C++ | Java
  • Infix to prefix conversion in –
    C | C++ | Java
  • Postfix to Prefix Conversion in –
    C | C++ | Java

Queues

  • Queues in Data Structures (Introduction)
    Click Here
  • Queues Program in C and implementation
    Click Here
  • Implementation of Queues using Arrays | C Program
    Click Here
  • Types of Queues in Data Structure
    Click Here
  • Application of Queue Data Structure
    Click Here
  • Insertion in Queues Program (Enqueuing) –
    C | C++ | Java
  • Deletion (Removal) in Queues Program(Dequeuing) –
    C | C++ | Java
  • Reverse a Queue –
    C | C++ | Java
  • Queues using Linked Lists –
    C | C++ | Java
  • Implement Queue using Stack –
    C | C++ | Java
  • Implement Queue using two Stacks –
    C | C++ | Java

Circular Queues

Priority Queue

  • Application of Priority Queue
  • Priority Queue Example
  • Priority Queue Introduction –
    C | C++ | Java
  • Priority Queue Implementation using Array –
    C | C++ | Java
  • Priority Queue using Linked List –
    C | C++ | Java
  • Priority Queue Insertion and Deletion-
    C | C++ | Java

Stacks

Queues

Circular Queues

Priority Queue

  • Application of Priority Queue
  • Priority Queue Example
  • Priority Queue Introduction – C | C++ | Java
  • Priority Queue Implementation using Array – C | C++ | Java
  • Priority Queue using Linked List – C | C++ | Java
  • Priority Queue Insertion and Deletion- C | C++ | Java