Infix to Postfix Conversion in Java
Infix to Postfix Conversion
Infix to Postfix Conversion in Java is a classic stack based problem that teaches you how compilers and calculators handle operator precedence and parentheses efficiently.
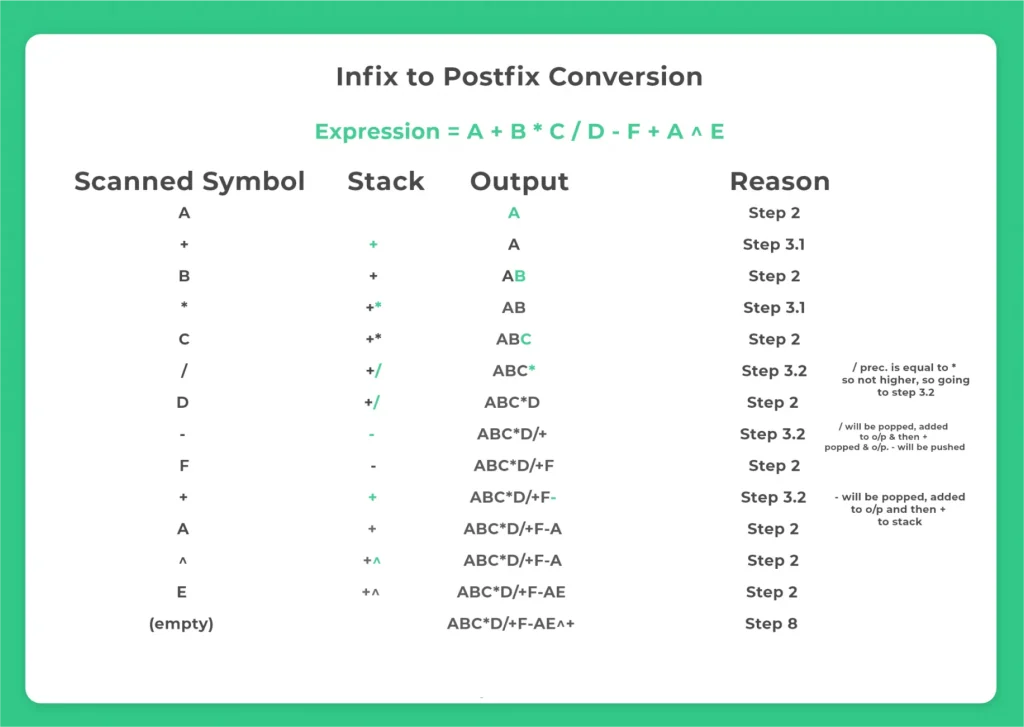
Infix is the normal format humans write (like A+B*C), while postfix (also called Reverse Polish Notation) places operators after operands (like ABC*+). Postfix is convenient for machines because it removes the need to handle precedence during evaluation.
Understand what Postfix & Infix is
- Infix Expression: When an operator is in between the two operands
- Example: A * B is known as infix expression.
- Postfix Expression: When operator is after the two operands
- Example: BD * is known as postfix expression.
Algorithm for Infix to Postfix in Java
Variables used:
- String infix → input expression
- Stack<Character> ops → operator stack
- StringBuilder postfix → output expression
Algorithm Steps:
- Initialize ops as empty, postfix as empty.
- For each character ch in infix:
If ch is an operand → append to postfix
Else if ch == ‘(‘ → push to ops
Else if ch == ‘)’ → pop from ops to postfix until ‘(‘ appears; pop ‘(‘
Else if ch is an operator:
- While ops not empty and top is operator and popping condition (precedence/associativity) holds:
- Pop ops to postfix
- Push ch to ops
- While ops not empty and top is operator and popping condition (precedence/associativity) holds:
After loop ends, pop remaining operators from ops to postfix.
postfix is the result.
Learn DSA
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Method to Implement Infix to Postfix in Java
- Use a stack to store operators and parentheses.
- Build postfix output in a string builder.
Note:
This version supports operands as single letters/digits (common in DSA problems). It also includes ^ as right-associative.
Java Code:
import java.util.Stack;
public class InfixToPostfix {
private static boolean isOperand(char ch) {
return Character.isLetterOrDigit(ch);
}
private static boolean isOperator(char ch) {
return ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '^';
}
private static int precedence(char op) {
switch (op) {
case '^': return 3;
case '*':
case '/': return 2;
case '+':
case '-': return 1;
default: return -1;
}
}
// ^ is right-associative, others are left-associative
private static boolean isRightAssociative(char op) {
return op == '^';
}
public static String convert(String infix) {
Stack ops = new Stack<>();
StringBuilder postfix = new StringBuilder();
for (int i = 0; i < infix.length(); i++) { char ch = infix.charAt(i); // Ignore spaces if (ch == ' ') continue; if (isOperand(ch)) { postfix.append(ch); } else if (ch == '(') { ops.push(ch); } else if (ch == ')') { while (!ops.isEmpty() && ops.peek() != '(') { postfix.append(ops.pop()); } // Pop '(' if (!ops.isEmpty() && ops.peek() == '(') ops.pop(); else throw new IllegalArgumentException("Mismatched parentheses"); } else if (isOperator(ch)) { while (!ops.isEmpty() && isOperator(ops.peek())) { char top = ops.peek(); // Pop if top has higher precedence // Or same precedence and current is left-associative if (precedence(top) > precedence(ch) ||
(precedence(top) == precedence(ch) && !isRightAssociative(ch))) {
postfix.append(ops.pop());
} else {
break;
}
}
ops.push(ch);
} else {
throw new IllegalArgumentException("Invalid character found: " + ch);
}
}
while (!ops.isEmpty()) {
if (ops.peek() == '(') throw new IllegalArgumentException("Mismatched parentheses");
postfix.append(ops.pop());
}
return postfix.toString();
}
public static void main(String[] args) {
String infix = "a*(b+c)/d";
String postfix = convert(infix);
System.out.println("Infix : " + infix);
System.out.println("Postfix : " + postfix);
}
}
Output:
Infix : a*(b+c)/d Postfix : abc+*d/
Space Complexity: O(n)
Common Edge Cases for Infix to Postfix in Java
- Mismatched parentheses should be detected and reported.
- Right associativity of ^ must be handled correctly (e.g., a^b^c becomes abc^^).
- If you need multi-digit numbers (like 12+34), tokenization is required (splitting input into numbers/operators instead of single characters).
Many beginner problems avoid this by using single letter operands.
Frequently Asked Questions
Answer:
Infix to Postfix Conversion in Java means converting a normal expression like A+B*C into postfix form ABC*+ using a stack to preserve precedence and parentheses.
Answer:
A stack temporarily stores operators and parentheses so we can output them in correct order based on precedence and associativity.
Answer:
Standard stack based method runs in O(n) time because each token is processed once and each operator is pushed and popped at most one time.
Answer:
( is pushed to the stack, and when ) is found, operators are popped to output until ( is reached; then ( is removed.
Answer:
Yes, but you must tokenize the input (read full numbers like 123 as one token). A character by character approach works best for single letter or single digit operands.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others






Login/Signup to comment