Tree Traversal : Inorder Preorder Postorder in Java
Tree Traversal : Inorder Preorder Postorder
In linear data structures like arrays and linked lists, we could traversel in one way but in tree data structures like binary tree, we can do tree traverse them in different ways. In this article we will learn about inorder, preorder and postorder traversal.

Tree Traversal : Inorder Preorder Postorder
Tree traversal is a process of visiting all the nodes in a tree data structure in a particular order. Tree traversal is used in many applications, including searching, sorting, and evaluating expressions. It is a fundamental concept in computer science and is essential for understanding and implementing various algorithms and data structures.
Example
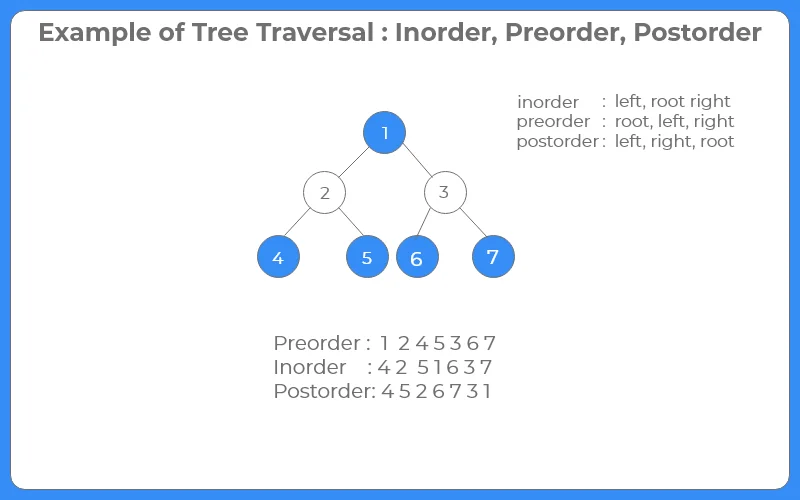
Different Tree Traversal Algorithms
Algorithm to Find Inorder Traversal
Algorithm inorder(tree)
- Recursively traverse left subtree.
- Visit root node.
- Recursively traverse right subtree.
Algorithm to find preorder traversal
Algorithm preorder(Tree):
- Visit root node.
- Recursively traverse left subtree.
- Recursively traverse right subtree.
Algorithm to find Postorder traversal
Algorihtm postorder(Tree):
- Recursively traverse left sub-tree.
- Recursively traverse right sub-tree.
- Visit root node.
Java code for implementing tree traversal
Run
class Node
{
int key;
Node left, right;
public Node (int item)
{
key = item;
left = right = null;
}
}
class BinaryTree
{
// Root of Binary Tree
Node root;
BinaryTree ()
{
root = null;
}
void postorder (Node ptr)
{
if (ptr == null)
return;
// first recur on left subtree
postorder (ptr.left);
// then recur on right subtree
postorder (ptr.right);
// now deal with the node
System.out.print (ptr.key + " ");
}
/* Given a binary tree, print its nodes in inorder*/
void inorder (Node ptr)
{
if (ptr == null)
return;
/* first recur on left child */
inorder (ptr.left);
/* then print the data of node */
System.out.print (ptr.key + " ");
/* now recur on right child */
inorder (ptr.right);
}
void preorder (Node ptr)
{
if (ptr == null)
return;
/* first print data of node */
System.out.print (ptr.key + " ");
/* then recur on left subtree */
preorder (ptr.left);
/* now recur on right subtree */
preorder (ptr.right);
}
}
public class Main
{
public static void main (String[]args)
{
BinaryTree tree = new BinaryTree ();
tree.root = new Node (1);
tree.root.left = new Node (2);
tree.root.right = new Node (3);
tree.root.left.left = new Node (4);
tree.root.left.right = new Node (5);
System.out.println ("Preorder traversal");
tree.preorder (tree.root);
System.out.println ("\nInorder traversal");
tree.inorder (tree.root);
System.out.println ("\nPostorder traversal");
tree.postorder (tree.root);
}
}
Output :
Preorder traversal
1 2 4 5 3
Inorder traversal
1 2 4 5 3
Postorder traversal
4 5 2 3 1
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Stacks
- Introduction to Stack in Data Structure
Click Here - Operations on a Stack
Click Here - Stack: Infix, Prefix and Postfix conversions
Click Here - Stack Representation in –
C | C++ | Java - Representation of a Stack as an Array. –
C | C++ | Java - Representation of a Stack as a Linked List. –
C | C++ | Java - Infix to Postfix Conversion –
C | C++ | Java - Infix to prefix conversion in –
C | C++ | Java - Postfix to Prefix Conversion in –
C | C++ | Java
Queues
- Queues in Data Structures (Introduction)
Click Here - Queues Program in C and implementation
Click Here - Implementation of Queues using Arrays | C Program
Click Here - Types of Queues in Data Structure
Click Here - Application of Queue Data Structure
Click Here - Insertion in Queues Program (Enqueuing) –
C | C++ | Java - Deletion (Removal) in Queues Program(Dequeuing) –
C | C++ | Java - Reverse a Queue –
C | C++ | Java - Queues using Linked Lists –
C | C++ | Java - Implement Queue using Stack –
C | C++ | Java - Implement Queue using two Stacks –
C | C++ | Java
Circular Queues
- Circular queue in Data Structure
Click Here - Applications of Circular Queues
Click Here - Circular queue in –
C | C++ | Java - Circular queue using Array –
C | C++ | Java - Circular Queue using Linked Lists –
C | C++ | Java
Priority Queue
Stacks
- Introduction to Stack in Data Structure
- Operations on a Stack
- Stack: Infix, Prefix and Postfix conversions
- Stack Representation in – C | C++ | Java
- Representation of a Stack as an Array. – C | C++ | Java
- Representation of a Stack as a Linked List. – C | C++ | Java
- Infix to Postfix Conversion – C | C++ | Java
- Infix to prefix conversion in – C | C++ | Java
- Postfix to Prefix Conversion in – C | C++ | Java
Queues
- Queues in Data Structures (Introduction)
- Queues Program in C and implementation
- Implementation of Queues using Arrays | C Program
- Types of Queues in Data Structure
- Application of Queue Data Structure
- Insertion in Queues Program (Enqueuing) – C | C++ | Java
- Deletion (Removal) in Queues Program(Dequeuing) – C | C++ | Java
- Reverse a Queue – C | C++ | Java
- Queues using Linked Lists – C | C++ | Java
- Implement Queue using Stack – C | C++ | Java
- Implement Queue using two Stacks – C | C++ | Java
Circular Queues
- Circular queue in Data Structure
- Applications of Circular Queues
- Circular queue in – C | C++ | Java
- Circular queue using Array – C | C++ | Java
- Circular Queue using Linked Lists – C | C++ | Java






Login/Signup to comment