Implementation of Stack in C++ (Introduction)
Introduction to Stack in Cpp
Stack Implementation in CPP – A stack is another type of Data Structure,generally implemented using arrays. Generally, the implementation is LIFO i.e. Last in First out .They are used to convert prefix expression into postfix expression , balanced parenthesis problem, finding preorder of a tree.
| Push Time Complexity | O(1) |
| Pop Time Complexity | O(1) |
| Display Time Complexity | O(n) |
| Space Complexity | O(n) |

Stack Data Structure in C++
A stack in C++ is a linear data structure that stores elements in a Last-In-First-Out (LIFO) manner. This means the element inserted last will be the first one to be removed.
- For ex – Think of it like a stack of plates — you can only take the top plate off first.
More about Implementation of Stack in C++
- Stack can be defined as a Data Structure that serves as saving the data in a particular fashion.
- In linear data structures like an array and linked list a user is allowed to insert or delete any element to and from any location respectively.
- However, in a Stack, both, insertion and deletion, is permitted at one end only.
- It works on the LIFO (Last In – First Out) basis, i.e, the first element that is inserted in the stack would be the last to be deleted; or the last element to be inserted in the stack would be the first to be deleted.
- It will be implemented in two ways –
- Array-based implementation
- Linked List based implementation
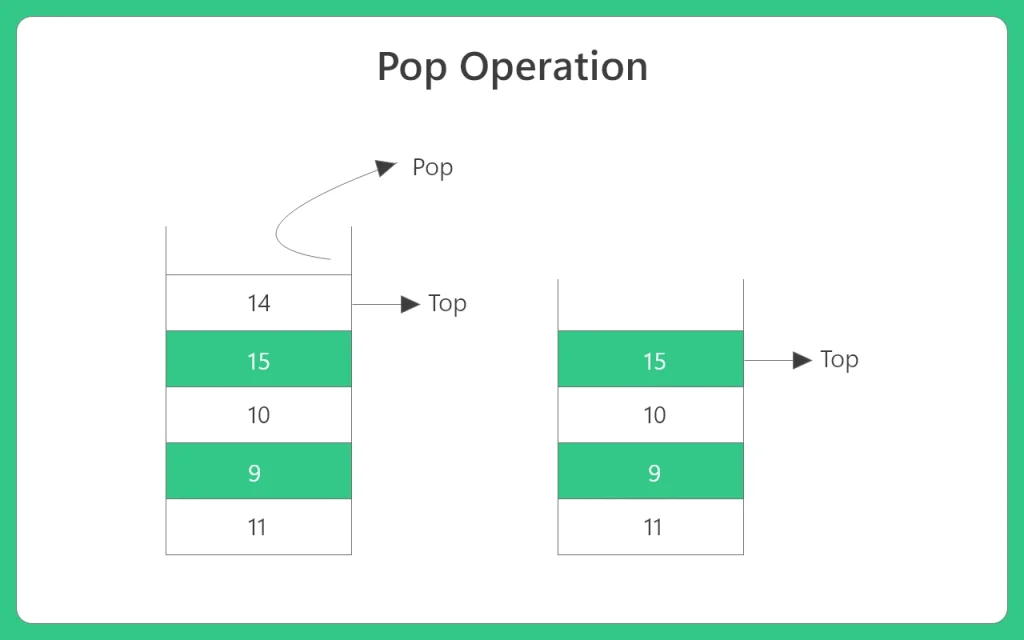
Stack Operations(Push, Pop, Display)
- Push: Adding a new item to the Stack Data Structure, in other words pushing new item to Stack DS. It is said to be in an overflow condition if the stack is full.
- Pop: Removing an item from the stack, i.e. popping an item out. If a stack is empty then it is said to be in an underflow condition
- Display: This basically display the whole stack.
Push Operation
Algorithm:
- Check whether stack is full or not.
- If the stack is full, it is not possible to add another element.
- Otherwise, create new node, store the data and change the pointer of top to the newly created node.

Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
C++ Program for Implementation of stack (array) using structure
The C++ program for implementing a stack using an array and structure demonstrates how to manage data in a Last-In-First-Out (LIFO) manner. It defines a structure to hold stack properties like top and array elements, along with operations such as push, pop, and display. This approach provides a clear understanding of stack behavior and memory handling using arrays in C++.
// C++ Program for Implmentation of stack (array) using structure
#include <limits.h>
#include <bits/stdc++.h>
using namespace std;
// A structure to represent a stack
struct Stack {
int top;
int maxSize;
int* array;
};
struct Stack* create(int max)
{
struct Stack* stack = (struct Stack*)malloc(sizeof(struct Stack));
stack->maxSize = max;
stack->top = -1;
stack->array = (int*)malloc(stack->maxSize * sizeof(int));
//here above memory for array is being created
// size would be 10*4 = 40
return stack;
}
// Checking with this function is stack is full or not
// Will return true is stack is full else false
//Stack is full when top is equal to the last index
int isFull(struct Stack* stack)
{
if(stack->top == stack->maxSize - 1){
cout<<"Will not be able to push maxSize reached\n"; } // Since array starts from 0, and maxSize starts from 1 return stack->top == stack->maxSize - 1;
}
// By definition the Stack is empty when top is equal to -1
// Will return true if top is -1
int isEmpty(struct Stack* stack)
{
return stack->top == -1;
}
// Push function here, inserts value in stack and increments stack top by 1
void push(struct Stack* stack, int item)
{
if (isFull(stack))
return;
stack->array[++stack->top] = item;
cout<<"We have pushed "<<item <<" to stack\n";
}
// Function to remove an item from stack. It decreases top by 1
int pop(struct Stack* stack)
{
if (isEmpty(stack))
return INT_MIN;
return stack->array[stack->top--];
}
// Function to return the top from stack without removing it
int peek(struct Stack* stack)
{
if (isEmpty(stack))
return INT_MIN;
return stack->array[stack->top];
}
int main()
{
struct Stack* stack = create(10);
push(stack, 5);
push(stack, 10);
push(stack, 15);
int flag=1;
while(flag)
{
if(!isEmpty(stack))
cout<<"We have popped"<< pop(stack)<<" from stack\n";
else
cout<<"Can't Pop stack must be empty\n";
flag=0;
}
return 0;
}
Output :
We have pushed 5 to stack We have pushed 10 to stack We have pushed 15 to stack We have popped 15 from the stack
Time and Space Complexity for Stack Implementation
| Operation | Time Complexity | Space Complexity |
|---|---|---|
| create() | O(1) | O(n) |
| isFull() | O(1) | O(1) |
| isEmpty() | O(1) | O(1) |
| push() | O(1) | O(1) |
| pop() | O(1) | O(1) |
| peek() | O(1) | O(1) |
| Overall | O(n) for n ops | O(n) |
Stack Implementation using Linked List in C++
A stack is a linear data structure that follows the Last In First Out (LIFO) principle. You can insert (push) and remove (pop) elements only from the top of the stack.
This implementation uses a singly linked list, where each element (node) contains two parts:
- data: The value of the stack element.
- next: A pointer to the next node in the stack.
The top of the stack is represented by the head (i.e., the first node) of the linked list.
C++ Code: Linked List-based Stack Implementation
#include<iostream>
using namespace std;
// Node structure
struct Node {
int data;
Node* next;
Node(int value) {
data = value;
next = nullptr;
}
};
// Stack class using Linked List
class Stack {
private:
Node* top; // Top of the stack
public:
Stack() {
top = nullptr;
}
// Push operation
void push(int value) {
Node* newNode = new Node(value);
newNode->next = top;
top = newNode;
cout << value << " pushed to stack\n";
}
// Pop operation
void pop() {
if (isEmpty()) {
cout << "Stack Underflow\n"; return; } Node* temp = top; top = top->next;
cout << "Popped element: " << temp->data << endl;
delete temp;
}
// Peek operation
int peek() {
if (isEmpty()) {
cout << "Stack is empty\n"; return -1; } return top->data;
}
// Check if the stack is empty
bool isEmpty() {
return top == nullptr;
}
// Display stack elements
void display() {
Node* current = top;
cout << "Stack elements: ";
while (current != nullptr) {
cout << current->data << " "; current = current->next;
}
cout << endl;
}
// Destructor to free memory
~Stack() {
while (!isEmpty()) {
pop();
}
}
};
// Driver code
int main() {
Stack s;
s.push(10);
s.push(20);
s.push(30);
s.display();
cout << "Top element is: " << s.peek() << endl;
s.pop();
s.display();
return 0;
}Output:
10 pushed to stack 20 pushed to stack 30 pushed to stack Stack elements: 30 20 10 Top element is: 30 Popped element: 30 Stack elements: 20 10
Time Complexity
- push() – O(1)
- pop() – O(1)
- peek() – O(1)
- isEmpty() – O(1)
- display() – O(n)
Space Complexity
- O(n) for storing n elements in the stack (each node holds data + pointer).
Explanation of the given Code
- Each element in the stack is a node that stores the value (data) and a pointer to the next node. These nodes are created using the Node structure.
- The Stack class keeps track of the top of the stack using a pointer called top. Initially, this is set to nullptr (empty stack).
- The push() function adds a new element to the top. It creates a new node, connects it to the current top, and then updates the top pointer to this new node.
- The pop() function removes the top element. It checks if the stack is empty. If not, it deletes the top node and moves the top pointer to the next node.
- The peek() function shows the top value without removing it. If the stack is empty, it returns -1 and shows a message.
- The display() function prints all elements from top to bottom by looping through the linked list. The isEmpty() function checks if the stack has any elements.
Conclusion
Using a linked list to implement a stack in C++ is a smart way to manage data when we don’t know the size in advance. It follows the Last In, First Out (LIFO) rule, meaning the last element added is the first to be removed. Unlike arrays, it doesn’t waste memory because it grows and shrinks as needed. All main operations like push, pop, and peek are fast and take constant time.
This method is simple, easy to understand, and helpful for learning pointers in C++. It’s also useful in many coding problems and real-world applications.
FAQs - Stack implementation using Linked List in C++
In real-time systems, we don’t always know how many elements will be stored. Arrays have a fixed size, but linked lists grow as needed. This avoids memory waste and overflow errors. Also, linked lists don’t require shifting or resizing, which makes operations faster and more predictable.
Both push and pop only change a few pointers:
- push adds a new node at the beginning
- pop removes the first node
These don’t depend on the number of elements, so the time complexity is always O(1), no matter how big the stack is.
Yes, memory leaks can happen if we don’t delete nodes properly. For example, forgetting to delete the top node during pop, or not freeing all nodes in the destructor.
- To prevent this, always use delete when removing a node and write a destructor that clears the whole stack.
If the stack is empty and we try to pop or peek, it can cause a crash or return garbage values. In this code, we’ve handled it safely using an isEmpty() check. This shows an error message and avoids breaking the program.
Recursion internally uses the system’s call stack, while manual stack (like this one) gives you more control. In large problems, manual stack is safer because recursion can cause stack overflow. So, for complex problems like DFS or maze solving, a linked list-based stack is often more stable and flexible.
Arrays have a fixed size, so you must decide the stack’s maximum capacity in advance. If more elements are pushed than the size allows, it causes stack overflow. Unlike linked lists, arrays can’t grow automatically, which limits their use in cases with unpredictable input sizes.
In array-based stacks, both push and pop take O(1) time. That’s because you’re just adding or removing an element at the top index without shifting any other elements. This makes basic stack operations fast and efficient.
- Overflow happens when you try to push into a full array.
- Underflow happens when you try to pop from an empty stack.
To handle these, always check the current size of the stack before performing push or pop
Yes, in some cases. Arrays don’t use extra memory for pointers, so they use less space per element. However, they can waste memory if the array is over-sized, or cause overflow if it’s too small. Linked lists use more memory per element but never waste space.
Yes, but not automatically like a linked list. You have to manually create a new larger array and copy the old elements. This resizing operation takes O(n) time, so it’s slow. That’s why array-based stacks are great when the size is known, but not ideal for dynamic data.
FAQs - Stack implementation using Linked List in C++
In real-time systems, we don’t always know how many elements will be stored. Arrays have a fixed size, but linked lists grow as needed. This avoids memory waste and overflow errors. Also, linked lists don’t require shifting or resizing, which makes operations faster and more predictable.
Both push and pop only change a few pointers:
- push adds a new node at the beginning
- pop removes the first node
These don’t depend on the number of elements, so the time complexity is always O(1), no matter how big the stack is.
Yes, memory leaks can happen if we don’t delete nodes properly. For example, forgetting to delete the top node during pop, or not freeing all nodes in the destructor.
- To prevent this, always use delete when removing a node and write a destructor that clears the whole stack.
If the stack is empty and we try to pop or peek, it can cause a crash or return garbage values. In this code, we’ve handled it safely using an isEmpty() check. This shows an error message and avoids breaking the program.
Recursion internally uses the system’s call stack, while manual stack (like this one) gives you more control. In large problems, manual stack is safer because recursion can cause stack overflow. So, for complex problems like DFS or maze solving, a linked list-based stack is often more stable and flexible.
Arrays have a fixed size, so you must decide the stack’s maximum capacity in advance. If more elements are pushed than the size allows, it causes stack overflow. Unlike linked lists, arrays can’t grow automatically, which limits their use in cases with unpredictable input sizes.
In array-based stacks, both push and pop take O(1) time. That’s because you’re just adding or removing an element at the top index without shifting any other elements. This makes basic stack operations fast and efficient.
- Overflow happens when you try to push into a full array.
- Underflow happens when you try to pop from an empty stack.
To handle these, always check the current size of the stack before performing push or pop
Yes, in some cases. Arrays don’t use extra memory for pointers, so they use less space per element. However, they can waste memory if the array is over-sized, or cause overflow if it’s too small. Linked lists use more memory per element but never waste space.
Yes, but not automatically like a linked list. You have to manually create a new larger array and copy the old elements. This resizing operation takes O(n) time, so it’s slow. That’s why array-based stacks are great when the size is known, but not ideal for dynamic data.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Stacks
- Introduction to Stack in Data Structure
Click Here - Operations on a Stack
Click Here - Stack: Infix, Prefix and Postfix conversions
Click Here - Stack Representation in –
C | C++ | Java - Representation of a Stack as an Array. –
C | C++ | Java - Representation of a Stack as a Linked List. –
C | C++ | Java - Infix to Postfix Conversion –
C | C++ | Java - Infix to prefix conversion in –
C | C++ | Java - Postfix to Prefix Conversion in –
C | C++ | Java
Queues
- Queues in Data Structures (Introduction)
Click Here - Queues Program in C and implementation
Click Here - Implementation of Queues using Arrays | C Program
Click Here - Types of Queues in Data Structure
Click Here - Application of Queue Data Structure
Click Here - Insertion in Queues Program (Enqueuing) –
C | C++ | Java - Deletion (Removal) in Queues Program(Dequeuing) –
C | C++ | Java - Reverse a Queue –
C | C++ | Java - Queues using Linked Lists –
C | C++ | Java - Implement Queue using Stack –
C | C++ | Java - Implement Queue using two Stacks –
C | C++ | Java
Circular Queues
- Circular queue in Data Structure
Click Here - Applications of Circular Queues
Click Here - Circular queue in –
C | C++ | Java - Circular queue using Array –
C | C++ | Java - Circular Queue using Linked Lists –
C | C++ | Java
Priority Queue
Stacks
- Introduction to Stack in Data Structure
- Operations on a Stack
- Stack: Infix, Prefix and Postfix conversions
- Stack Representation in – C | C++ | Java
- Representation of a Stack as an Array. – C | C++ | Java
- Representation of a Stack as a Linked List. – C | C++ | Java
- Infix to Postfix Conversion – C | C++ | Java
- Infix to prefix conversion in – C | C++ | Java
- Postfix to Prefix Conversion in – C | C++ | Java
Queues
- Queues in Data Structures (Introduction)
- Queues Program in C and implementation
- Implementation of Queues using Arrays | C Program
- Types of Queues in Data Structure
- Application of Queue Data Structure
- Insertion in Queues Program (Enqueuing) – C | C++ | Java
- Deletion (Removal) in Queues Program(Dequeuing) – C | C++ | Java
- Reverse a Queue – C | C++ | Java
- Queues using Linked Lists – C | C++ | Java
- Implement Queue using Stack – C | C++ | Java
- Implement Queue using two Stacks – C | C++ | Java
Circular Queues
- Circular queue in Data Structure
- Applications of Circular Queues
- Circular queue in – C | C++ | Java
- Circular queue using Array – C | C++ | Java
- Circular Queue using Linked Lists – C | C++ | Java





Login/Signup to comment