Queue Data Structure (Introduction)

Queue Introduction
A Queue is another type of Data Structure, generally done via arrays. Generally, Queues are FIFO i.e. First in First out. A good example would be people standing at a billing counter in a queue, the person who comes first, will be served first
More about Queues
- Unlike arrays, where insertion and deletion can happen at any end.
- In Queues, insertion (Enqueue) and deletion (Dequeue) can happen at only one end each.
- Insertion happens at the rear end and deletion happens at the front
- Queues follow FIFO First in First out structure, i.e. the element added first (Enqueued) will go out of the queue first(Dequeued)
- Unlike stack, which follows, LIFO, last in first out, and stack where both insertion and deletion happens as one end. For queue insertion(Enqueue) and deletion(Dequeue) happens at opposite ends.
Queue Operations
- Enqueue: Adding a new item to the Queue Data Structure, in other words, enqueuing new item to Stack DS.
If the Queue is full, then it is said to be in an overflow condition
- Dequeue: Removing an item from the Queue, i.e. dequeuing an item out.
If a Queue is empty then it is said to be in an underflow condition
- IsEmpty: This returns True If the Queue is empty else returns False
- IsFull: This returns True if the Queue is full else returns false.
Some other notations are Front and Rear, that return the front end read items of the queue.
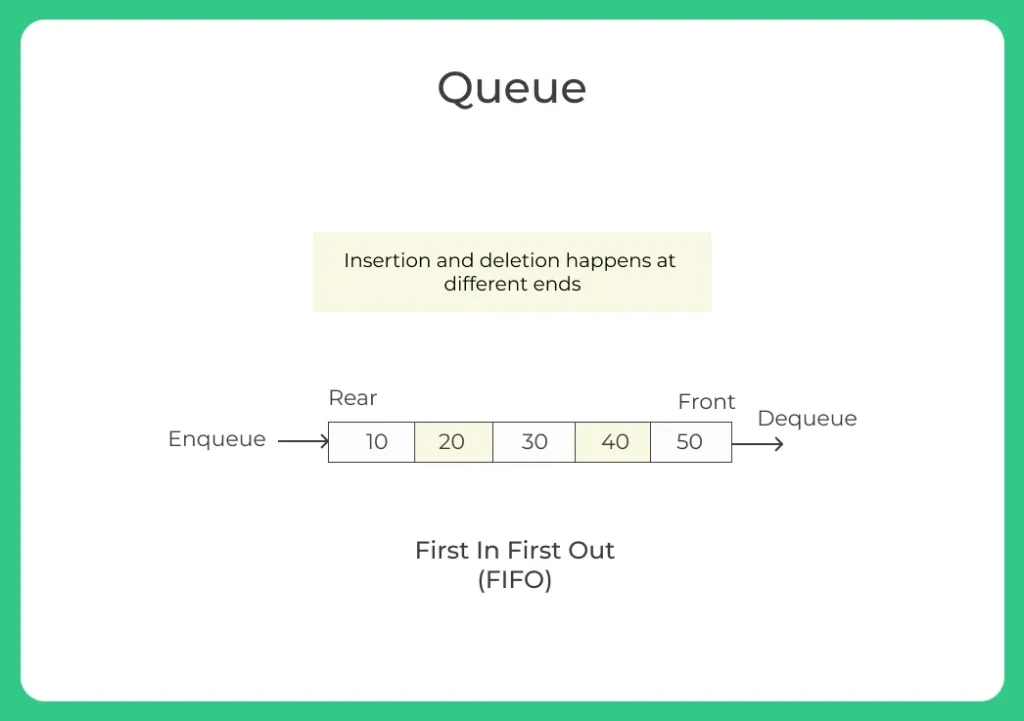
Representation of Queue
Queue as a data structure can be represented in two ways.
- Stack as an Array (Most popular)
- Stack as a struct (Popular)
- Stack as a Linked List.
Very Important Note
The given diagram of enqueueing, dequeue and even the code for queues is given wrong on GeeksforGeeks and all other websites.
As these website's codes are written by interns and not teachers.
As these website's codes are written by interns and not teachers.
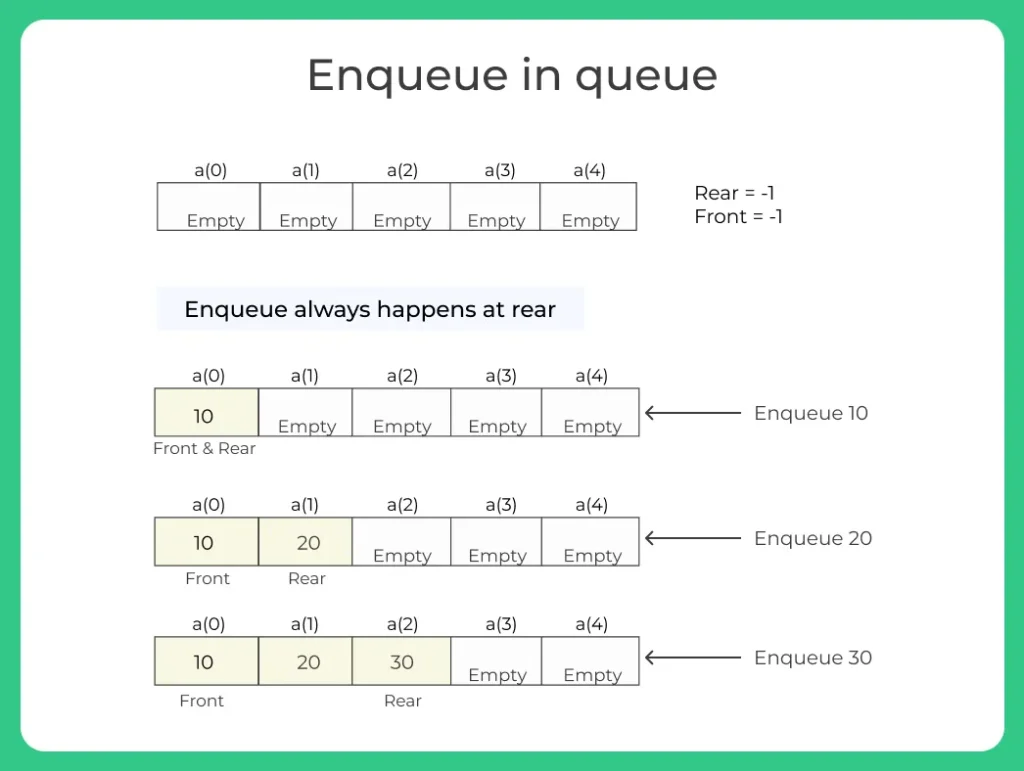
1. Enqueue()
- When we require to add an element to the Queue we perform Enqueue() operation.
- Push() operation is synonymous of insertion/addition in a data structure.
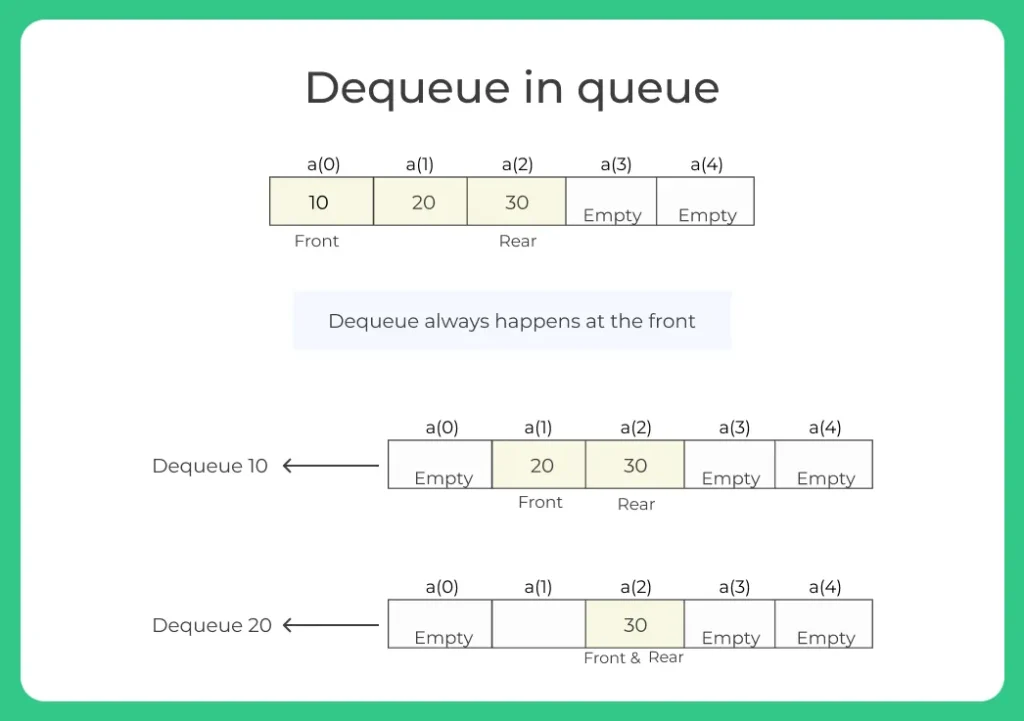
2. Dequeue()
- When we require to delete/remove an element to the Queue we perform Dequeue() operation.
- Dequeue() operation is synonymous of deletion/removal in a data structure.
Applications and uses for Queues
- Heavily used in almost all applications of the operating system, to schedule processes, moving them in or out of process scheduler.
- FCFS, SJF etc
- Asynchronously i.e. when data resource may be the same but not received at the same rate.
- Anything that has to do with process and schedule, in the system or code.
Run
#include <bits/stdc++.h>
using namespace std;
// A structure to represent a queue
class Queue {
public:
int front, rear, size;
unsigned capacity;
int* array;
};
// function to create a queue
// of given capacity.
// It initializes size of queue as 0
Queue* createQueue(unsigned capacity)
{
Queue* queue = new Queue();
queue->capacity = capacity;
queue->front = queue->size = 0;
// This is important, see the enqueue
queue->rear = capacity - 1;
queue->array = new int[queue->capacity];
return queue;
}
// Queue is full when size
// becomes equal to the capacity
int isFull(Queue* queue)
{
return (queue->size == queue->capacity);
}
// Queue is empty when size is 0
int isEmpty(Queue* queue)
{
return (queue->size == 0);
}
// Function to add an item to the queue.
// It changes rear and size
void enqueue(Queue* queue, int item)
{
if (isFull(queue))
return;
queue->rear = (queue->rear + 1)
% queue->capacity;
queue->array[queue->rear] = item;
queue->size = queue->size + 1;
cout << item << " enqueued to queue\n";
}
// Function to remove an item from queue.
// It changes front and size
int dequeue(Queue* queue)
{
if (isEmpty(queue))
return INT_MIN;
int item = queue->array[queue->front];
queue->front = (queue->front + 1)
% queue->capacity;
queue->size = queue->size - 1;
return item;
}
// Function to get front of queue
int front(Queue* queue)
{
if (isEmpty(queue))
return INT_MIN;
return queue->array[queue->front];
}
// Function to get rear of queue
int rear(Queue* queue)
{
if (isEmpty(queue))
return INT_MIN;
return queue->array[queue->rear];
}
// Driver code
int main()
{
Queue* queue = createQueue(1000);
enqueue(queue, 10);
enqueue(queue, 20);
enqueue(queue, 30);
enqueue(queue, 40);
cout << dequeue(queue)
<< " dequeued from queue\n";
cout << "Front item is "
<< front(queue) << endl;
cout << "Rear item is "
<< rear(queue) << endl;
return 0;
}10 enqueued to queue 20 enqueued to queue 30 enqueued to queue 40 enqueued to queue 10 dequeued from queue Front item is 20 Rear item is 40
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Stacks
- Introduction to Stack in Data Structure
Click Here - Operations on a Stack
Click Here - Stack: Infix, Prefix and Postfix conversions
Click Here - Stack Representation in –
C | C++ | Java - Representation of a Stack as an Array. –
C | C++ | Java - Representation of a Stack as a Linked List. –
C | C++ | Java - Infix to Postfix Conversion –
C | C++ | Java - Infix to prefix conversion in –
C | C++ | Java - Postfix to Prefix Conversion in –
C | C++ | Java
Queues
- Queues in Data Structures (Introduction)
Click Here - Queues Program in C and implementation
Click Here - Implementation of Queues using Arrays | C Program
Click Here - Types of Queues in Data Structure
Click Here - Application of Queue Data Structure
Click Here - Insertion in Queues Program (Enqueuing) –
C | C++ | Java - Deletion (Removal) in Queues Program(Dequeuing) –
C | C++ | Java - Reverse a Queue –
C | C++ | Java - Queues using Linked Lists –
C | C++ | Java - Implement Queue using Stack –
C | C++ | Java - Implement Queue using two Stacks –
C | C++ | Java
Circular Queues
- Circular queue in Data Structure
Click Here - Applications of Circular Queues
Click Here - Circular queue in –
C | C++ | Java - Circular queue using Array –
C | C++ | Java - Circular Queue using Linked Lists –
C | C++ | Java
Priority Queue
Stacks
- Introduction to Stack in Data Structure
- Operations on a Stack
- Stack: Infix, Prefix and Postfix conversions
- Stack Representation in – C | C++ | Java
- Representation of a Stack as an Array. – C | C++ | Java
- Representation of a Stack as a Linked List. – C | C++ | Java
- Infix to Postfix Conversion – C | C++ | Java
- Infix to prefix conversion in – C | C++ | Java
- Postfix to Prefix Conversion in – C | C++ | Java
Queues
- Queues in Data Structures (Introduction)
- Queues Program in C and implementation
- Implementation of Queues using Arrays | C Program
- Types of Queues in Data Structure
- Application of Queue Data Structure
- Insertion in Queues Program (Enqueuing) – C | C++ | Java
- Deletion (Removal) in Queues Program(Dequeuing) – C | C++ | Java
- Reverse a Queue – C | C++ | Java
- Queues using Linked Lists – C | C++ | Java
- Implement Queue using Stack – C | C++ | Java
- Implement Queue using two Stacks – C | C++ | Java
Circular Queues
- Circular queue in Data Structure
- Applications of Circular Queues
- Circular queue in – C | C++ | Java
- Circular queue using Array – C | C++ | Java
- Circular Queue using Linked Lists – C | C++ | Java






is there going to be any ph test of elitmus during December?
Yeah Mansi, there are chances for that to happen
Have any questions ? Ask us in the comment section 🙂