Postfix to Prefix Conversion using Stack in C (C Program)
Postfix to Prefix
As we already know that any give operation in compiler can be expressed in 3 ways which are Infix, postfix and prefix, we shall see how to convert postfix to prefix operation via manual calculation and via code.

What postfix, infix, prefix rules are –
- Infix: (X + Y)
- Postfix – The postfix will look like, XY+
- Prefix: The prefix will look like, +YX
Infix : (X + Y) / (U – V)
- Postfix – The postfix will look like, XY+UV-/
- Prefix – The prefix will look like, /+XY-UV
If we want to get postfix to infix all of us generally convert postfix to the infix and then convert Infix to prefix, as this is easier to do, and even we recommend to do the same.
- What when Postfix is given and you want to calculate Prefix directly?
- Or if you want to code the same doing temporary conversion to Infix will be time-consuming and longer code will be there.
Following is the algorithm-
A + B, where A and B are operands and + is operator, the whole A + B is expression.
- Start reading the expression from L – R i.e. Left to right
- If you encounter an operand, then do push in the stack
- If we encounter an operator then, pop two operands from the stack, and concatenate them, in +AB type of format
- And push the resultant sting back to the stack
- Repeat the above steps till end of the expression
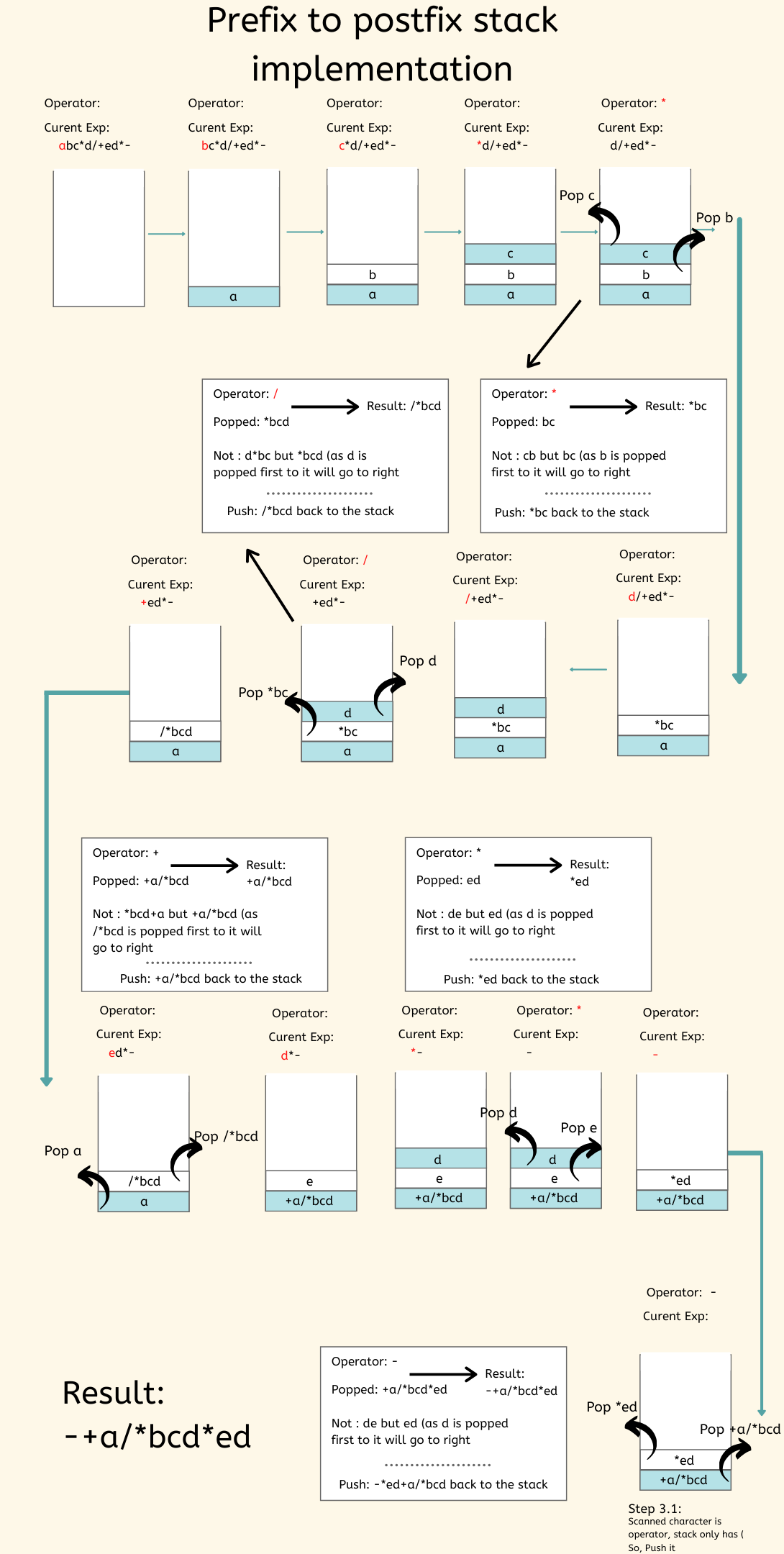
- Postfix: abc*d/+ed*-
- Prefix: -+a/*bcd*ed
- Infix: ((a+((b*c)/d))-(e*d))
Below is an implementation for it
Code for Postfix to Prefix in C
However, to code, we will apply different logic as it is difficult to push into the stack when we have a 2D array in C. For example, pushing a character ‘a’ is fine but pushing *bc which is a string and in a stack which already is an array needs 2D array so, we use other implementation in C. Please follow the code below and you will understand how this implementation works.
Note – It has a different logic than the above rule explained.
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define MAX 20
char str[MAX], stack[MAX];
int top = -1;
void push (char c)
{
stack[++top] = c;
}
char pop ()
{
return stack[top--];
}
// A utility function to check if the given character is operand
int checkIfOperand (char ch)
{
return (ch >= 'a' && ch <= 'z') || (ch >= 'A' && ch <= 'Z');
}
//function to check if it is an operator
int isOperator (char x)
{
switch (x)
{
case '+':
case '-':
case '/':
case '*':
return 1;
}
return 0;
}
void postfixToprfix ()
{
int n, i, j = 0;
char c[20];
char a, b, op;
printf ("Enter the postfix expression\n");
scanf ("%s", str);
n = strlen (str);
for (i = 0; i < MAX; i++)
stack[i] = '\0';
printf ("Prefix expression is: ");
for (i = n - 1; i >= 0; i--)
{
if (isOperator (str[i]))
{
push (str[i]);
}
else
{
c[j++] = str[i];
while ((top != -1) && (stack[top] == '#'))
{
a = pop ();
c[j++] = pop ();
}
push ('#');
}
}
c[j] = '\0';
i = 0;
j = strlen (c) - 1;
char d[20];
while (c[i] != '\0')
{
d[j--] = c[i++];
}
printf ("%s\n", d);
}
int main ()
{
postfixToprfix ();
return 0;
}
Output
Enter the postfix expression ab+cd-* Prefix expression is: *+ab-cd
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Stacks
- Introduction to Stack in Data Structure
- Operations on a Stack
- Stack: Infix, Prefix and Postfix conversions
- Stack Representation in – C | C++ | Java
- Representation of a Stack as an Array. – C | C++ | Java
- Representation of a Stack as a Linked List. – C | C++ | Java
- Infix to Postfix Conversion – C | C++ | Java
- Infix to prefix conversion in – C | C++ | Java
- Postfix to Prefix Conversion in – C | C++ | Java
Queues
- Queues in Data Structures (Introduction)
- Queues Program in C and implementation
- Implementation of Queues using Arrays | C Program
- Types of Queues in Data Structure
- Application of Queue Data Structure
- Insertion in Queues Program (Enqueuing) – C | C++ | Java
- Deletion (Removal) in Queues Program(Dequeuing) – C | C++ | Java
- Reverse a Queue – C | C++ | Java
- Queues using Linked Lists – C | C++ | Java
- Implement Queue using Stack – C | C++ | Java
- Implement Queue using two Stacks – C | C++ | Java
Circular Queues
- Circular queue in Data Structure
- Applications of Circular Queues
- Circular queue in – C | C++ | Java
- Circular queue using Array – C | C++ | Java
- Circular Queue using Linked Lists – C | C++ | Java
Priority Queue
Stacks
- Introduction to Stack in Data Structure
Click Here - Operations on a Stack
Click Here - Stack: Infix, Prefix and Postfix conversions
Click Here - Stack Representation in –
C | C++ | Java - Representation of a Stack as an Array. –
C | C++ | Java - Representation of a Stack as a Linked List. –
C | C++ | Java - Infix to Postfix Conversion –
C | C++ | Java - Infix to prefix conversion in –
C | C++ | Java - Postfix to Prefix Conversion in –
C | C++ | Java
Queues
- Queues in Data Structures (Introduction)
Click Here - Queues Program in C and implementation
Click Here - Implementation of Queues using Arrays | C Program
Click Here - Types of Queues in Data Structure
Click Here - Application of Queue Data Structure
Click Here - Insertion in Queues Program (Enqueuing) –
C | C++ | Java - Deletion (Removal) in Queues Program(Dequeuing) –
C | C++ | Java - Reverse a Queue –
C | C++ | Java - Queues using Linked Lists –
C | C++ | Java - Implement Queue using Stack –
C | C++ | Java - Implement Queue using two Stacks –
C | C++ | Java
Circular Queues
- Circular queue in Data Structure
Click Here - Applications of Circular Queues
Click Here - Circular queue in –
C | C++ | Java - Circular queue using Array –
C | C++ | Java - Circular Queue using Linked Lists –
C | C++ | Java






Login/Signup to comment