InfyTQ Advantage Coding Round Question 2024
InfyTQ Advantage Round Coding
Question with Solutions PDF 2024
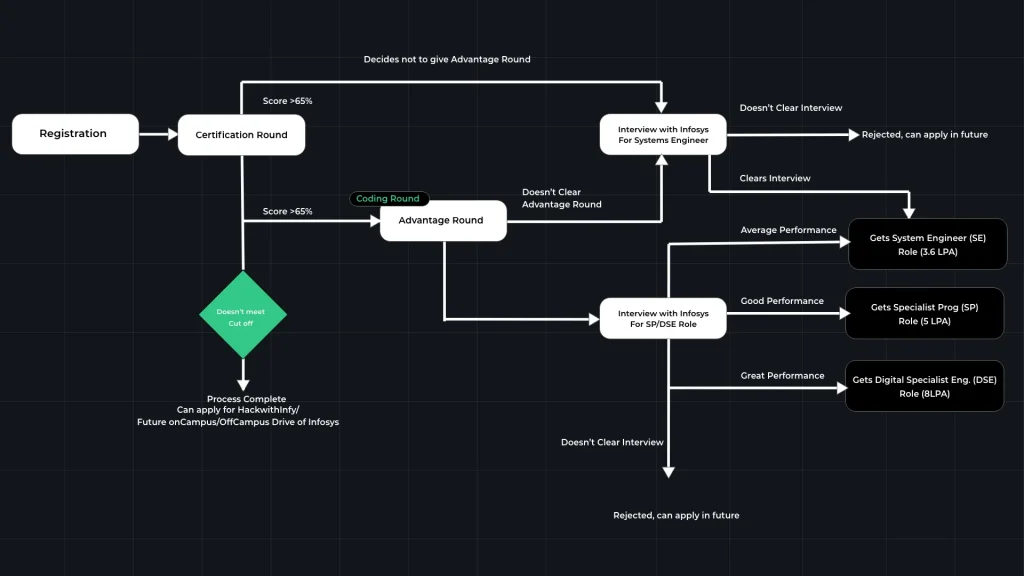
InfyTQ Advantage Round is an optional round for the candidates who will qualify the Certificate round(score >65%). This round is a coding test round, where you will have 3 coding questions with varied difficulty level. The better you perform in this round, the chances of a better package increases.

Pattern for InfyTQ Advantage Round
- There will be 3 coding questions in this round, with varied difficulty level.
- Each question will have a different weight-age of marks, depending upon the difficulty level of that question.
- You will be able to solve the questions only either in Java or Python, depending upon the language that you would have chosen at the time of booking the slots.
- Clearing the Advantage round will give you a chance for a pre-replacement interview either for the post of Power Programmer or System Engineer Specialist based on their performance in the interview.
Detailed analysis for InfyTQ Advantage Coding Round
| Topics | No. of Questions |
|---|---|
| Number of Questions | 3 |
| Time Limit | 3 hrs(combined with MCQ) |
| Difficulty level | very high |
| Package Offered | 5 LPA – 8 LPA |
InfyTQ Advantage Round Practice Coding Questions
Question 1: TOR
Problem Statement-: Lets define Ternary numbers to be the positive integer numbers that consist of digits 0,1,2 only. Let’s also define the operation TOR(x,y) to be the following operation on two Trenary numbers x and y (its output is z = TOR(x,y)).
- Go through the digits one by one .
- For each digit i, the digit i in the output will be z[i] = (x[i] + y[i]) % 3
You are given a positive integer n, and a long positive integer c, your job is to find two Ternary numbers a,b (of length n) where c = TOR(a,b) and max(a,b) is as minimum as possible. After finding that pair output max(a,b). If there’s no such pair, output -1.
- Note 1: the given numbers won’t have any leading zeros.
- Note 2: a,b should be of length n without leading zeros.
- Note 3: since the answer can be very large, output it modulo 1000000007 (10^9 +7).
Function Description:
Complete the TOR function in the editor below. It has the following parameters(s):
Parameters:
| Name | Type | Description |
|---|---|---|
| n | integer | The length of a and b |
| c | string | The number which should satisfy the equation c=TOR(a,b). |
The function must return an INTEGER denoting the max(a,b) when it’s minimized.
Constraints:
- 1 <= n <= 10^5
- 1 <= len(c) <= 2*n
Input Format
- The first line contains an integer, n, denoting the length of a and b .
- The next line contains a string, c, denoting the number which should satisfy the equation c=TOR(a,b).
Sample Cases:
- Sample input 1
2
22 - Sample output
11
#include<bits/stdc++.h>
using namespace std;
string s;
int n;
bool ch;
int fun(int i,int num)
{
if(i==s.length()) return num;//cout<<num<<endl;
if(ch) return fun(i+1,num*10);
if(s[i]=='0') return fun(i+1,num*10);
if(s[i]=='2') return fun(i+1,num*10 + 1);
if(i==0) return fun(i+1,2);
ch=true;
return fun(i+1,num*10+1);
}
int main()
{
cin>>n;
ch=false;
cin>>s;
cout << fun(0,0)%1000000007;
}
ch=False
n=int(input())
s=input()
def fun(i,num,ch):
if i==n:
return num
if ch:
return fun(i+1,num*10,ch)
if s[i]=='0':
return fun(i+1,num*10,ch)
if s[i]=='2':
return fun(i+1,num*10+1,ch)
if i==0:
return fun(i+1,2,ch)
ch=True
return fun(i+1,num*10+1,ch)
print(fun(0,0,ch))
import java.util.*;
class Main {
static String s;
static int n;
static Boolean ch;
static int fun(int i, int num) {
if (i == s.length())
return num;
if (ch)
return fun(i + 1, num * 10);
if (s.charAt(i) == '0')
return fun(i + 1, num * 10);
if (s.charAt(i) == '2')
return fun(i + 1, num * 10 + 1);
if (i == 0)
return fun(i + 1, 2);
ch = true;
return fun(i + 1, num * 10 + 1);
}
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
s = sc.next();
ch = false;
System.out.println(fun(0, 0) % 1000000007);
}
}Question 2 : Special LIS
Problem statement-: Given an array of N integers. Find the length of the longest increasing subsequence such that the difference between adjacent elements of the longest increasing subsequence is also increasing.
Note: It’s not required that the sequence should have strictly increasing numbers and the differences are also not required to be strictly increasing.
Ex: [1,2,3,4,5]. The longest increasing subsequence will be [1,2,4,5] but the difference array in this case is [1,2,1] which is not increasing. If we consider [1,2,4] or [1,2,5] then the numbers as well as the differences are in increasing order.
Function Description:
Complete the specialLIS function in the editor below. It has the following parameter(s):
Parameters:
| Name | Type | Type |
|---|---|---|
| size | Integer | size of array |
| arr | Integer array | array |
Return:
The function must return an INTEGER denoting the length of the longest increasing sub sequence with increasing differences.
Constraints:
- 1 <= size <= 500
- 1 <= arr[i] <= 10^5
Input Format:
- The first line contains integer, size, denoting the size of the array.
- Each line i of the size subsequent lines (where 0 <= i < size) contains an integer describing the ith elements of the array.
Sample Cases
- Sample Input 1
5
1
2
3
4
5
- Sample Output 1
5
#include<bits/stdc++.h>
using namespace std;
int n;
map<int,map<int,map<int,map<int,int>>>> m;
int fun(int i,int le,int d,int i1,vector a)
{
if(m[i][le][d][i1]) return m[i][le][d][i1];
if(i==n) return m[i][le][d][i1]=le;
if(le==0) return m[i][le][d][i1]=max(fun(i+1,1,0,i,a),fun(i+1,0,0,i+1,a));
if(a[i]-a[i1]>=d) return m[i][le][d][i1]=max(fun(i+1,le+1,a[i]-a[i1],i,a),fun(i+1,le,d,i1,a));
return m[i][le][d][i1]=fun(i+1,le,d,i1,a);
}
int main()
{
cin>>n;
vector a(n);
for(int i=0;i<n;i++) cin>>a[i];
cout<<fun(0,0,0,0,a);
}n=int(input())
a=[]
for i in range(n):
a.append(int(input()))
dp=[[[[-2 for i in range(n+1)] for j in range((max(a)-min(a)+2))] for k in range(n+1)] for l in range(n+1)]
def answer(i,le,d,i1):
if dp[i][le][d][i1]!=-2:
return dp[i][le][d][i1]
if i==n:
dp[i][le][d][i1]=le
return dp[i][le][d][i1]
else:
if le==0:
dp[i][le][d][i1] = max(answer(i+1,1,0,i),answer(i+1,0,0,i+1))
return dp[i][le][d][i1]
else:
if (a[i]-a[i1])>=d:
dp[i][le][d][i1]= max(answer(i+1,le+1,(a[i]-a[i1]),i),answer(i+1,le,d,i1))
return dp[i][le][d][i1]
else:
dp[i][le][d][i1]= answer(i+1,le,d,i1)
return dp[i][le][d][i1]
print(answer(0,0,0,0))
import java.util.*;
public class Main{
public static void main(String[]args) {
Scanner sc = new Scanner(System.in);
System.out.println("enter the size of the array");
int n =sc.nextInt();
int[] arr = new int[n];
System.out.println("Elements are not of original array");
for (int i = 0;i<arr.length; i++) {
arr[i]=sc.nextInt();
}
System.out.println(lis(arr,n));
}
static int lis(int[] arr, int n)
{
int lis[] = new int[n];
int i, j, max = 0;
// Initialize LIS values for all indexes /
for (i = 0; i < n; i++)
lis[i] = 1;
// Compute optimized LIS values in
//bottom up manner /
for (i = 1; i < n; i++)
for (j = 0; j < i; j++)
if (arr[i] > arr[j] && lis[i] < lis[j] + 1)
lis[i] = lis[j] + 1;
//Pick maximum of all LIS values */
for (i = 0; i < n; i++)
if (max < lis[i])
max = lis[i];
return max;
}
}Question 3: Alisa In the Library
Problem Statement -: Alisa is in the library, she wants to buy some different books, there are “nm” different chemistry books and k different science books. In how many different ways can Alisa select a book of mathematics, two books of chemistry, and some books of science?
Function Description:
- Complete the books function in the editor below. It has the following parameter(s):
Parameters:
| Name | Type | Description |
|---|---|---|
| n | Integer | the number of mathematics books |
| m | Integer | the number of chemistry books |
| k | Integer | the number of science books |
| x | Integer | the number of books of science Alisa needs |
Return: The function must return an INTEGER denoting the number of ways Alisa can buy the books she needs.
Constraints:
- 1 <= n <= 10^6
- 1 <= m <= 10^6
- 1 <= k <= 10^6
- 1 <= x <= 10^6
Input Format:
- The first line contains an integer, n, denoting the number of mathematics books.
- The next line contains an integer, m, denoting the number of chemistry books.
- The next line contains an integer, k, denoting the number of science books.
- The next line contains an integer, x, denoting the number of books of science Alisa needs.
OUTPUT DESCRIPTION
We have 5 different mathematics books, four different chemistry books, and two different science books which we have to choose all of them (d=2) so, we can choose 1 book out of five mathematics books in 5 ways, 2 out of 4 chemistry books in 6 ways, and we have only one way to choose 2 out of 2 science books, total: 5*6*1 = 30 ways.
Sample Test Cases
- Sample Input 1
5
4
2
2 - Sample Output 1
30
#include <bits/stdc++.h>
using namespace std;
int comb(int c,int d,int cc,int dd)
{
if(d==1) return cc*c/dd;
return comb(c-1,d-1,cc*c,dd*d);
}
int main()
{
int a,b,c,d;
cin>>a>>b>>c>>d;
if(a<1||b<2||c<d) {cout<<0;return 0;}
int ans=1;
ans*=a;
ans=ans*b*(b-1)/2;
ans*=comb(c,d,1,1);
cout<<ans;
}
>def comb(c,d,cc,dd):
if d==1:
return cc*c//dd
return comb(c-1,d-1,cc*c,dd*d)
a=int(input())
b=int(input())
c=int(input())
d=int(input())
if a<1 or b<2 or c<d:
print(0)
else:
ans=1
ans*=a
ans=ans*b*(b-1) // 2
ans*=comb(c,d,1,1)
print(ans)
import java.util.*;
class Main {
static int comb(int c, int d, int cc, int dd) {
if (d == 1) return cc * c / dd;
return comb(c - 1, d - 1, cc * c, dd * d);
}
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
int a, b, c, d;
a = sc.nextInt();
b = sc.nextInt();
c = sc.nextInt();
d = sc.nextInt();
if (a < 1 || b < 2 || c < d) {
System.out.println("0");
}
else {
int ans = 1;
ans *= a;
ans = ans * b * (b - 1) / 2;
ans *= comb(c, d, 1, 1);
System.out.println(ans);
}
}
}Question 4: Palindromic Paths
Problem Statement-: You are given a grid of size of N*M (1-based indexing). Each cell in the grid contains a lower case English alphabet (a-z). You have to replace some letters of the grid such that any path from (1,1) to (N,M) is a palindromic path. A path is palindromic if the string obtained by joining letters from the corresponding cells of a traversed path is a palindrome i.e. reads the same forward and backward. You are only allowed to move Right or Down in the grid.
Calculate the minimum number of letters that you need to replace such that any valid path from (1,1) to (N,M) is palindromic.
Function Description:
Complete the palindromicPaths function in the editor below. It has the following parameter(s):
Parameters:
| Name | Type | Description |
|---|---|---|
| n | Integer | Number of rows in the grid |
| m | Integer | number of columns in the grid |
| grid | string 2D array | the given grid |
Return: The function must return an integer denoting the minimum number of letters.
Constraints:
- 1 <= N <= 10^3
- 1 <= M <= 10^3
- a <= grid[i][j] <= z
Input format for Custom Testing:
- The first line contains an integer, N, denoting the number of rows in the grid.
- The next line contains an integer, M, denoting the number of columns in the grid.
- Each line i of the N subsequent lines (where 0 <= i <N) contains a string of lower-case English Alphabets of size M.
Sample Test Cases
- Sample Input
2
2
ac
bc - Sample Output
1 - Explanation
Change the letter at (2,2) to ‘a’, such that both paths become palindromes.
Path1: (1,1) -> (1,2) -> (2,2)
Path2: (1,1) -> (2,1) -> (2,2)
#include <bits/stdc++.h>
using namespace std;
int func(vector<vector> mat)
{
int ans=0;
int n=mat.size(),m=mat[0].size();
map<int,map<int,int>> mp;
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
{
int ind =i+j;
mp[ind][mat[i][j]]++;
}
int r=m+n-2,l=0;
while(l<r)
{
int t=0,mx=0;
for(auto x:mp[r])
{
mp[l][x.first]+=x.second;
}
for(auto x:mp[l])
{
t+=x.second;
mx=max(x.second,mx);
}
ans+=t-mx;
l++;
r--;
}
return ans;
}
int main()
{
int N,M;
string s;
cin>>N>>M;
vector<vector> mat(N,vector(M));
for(int i=0;i<N;i++)
{
cin>>s;
for(int j=0;j<M;j++)
mat[i][j]=s[j]-'a';
}
cout<<func(mat);
}
def m(lis,n):
d1=dict()
for i in lis:
if i in d1:
d1[i]+=1
else:
d1[i]=1
m1=0
for i in d1:
m1=max(m1,d1[i])
return (n-m1)
r=int(input())
c=int(input())
a=[]
for i in range(r):
b=list(input())
a.append(b)
d=dict()
t=r+c-2
d=dict()
for i in range(r):
for j in range(c):
t1=min((i+j),(t-(i+j)))
if t1 in d:
d[t1].append(a[i][j])
else:
d[t1]=[a[i][j]]
ans=0
for i in d:
if (i*2)!=t:
lis=d[i]
n=len(d[i])
ans+=m(lis,n)
print(ans)
Question 5: Divisible by K
Problem Statement-: Alice has a non-negative integer x written in the base y (a numeral system where 2 <= y <= 16). The number x has distinct digits. Bob has a number k written in the decimal numeral system. Alice wanted to check if the number x is divisible by the number k. However, Bob thinks it’s a very easy task. That’s why he proposed another problem: count the number of permutations of x which result in a number divisible by k.
Alice is confused and doesn’t know how to solve Bob’s problem, can you help her?
Notes:
- y is given in decimal.
- The possible digits for x start with the usual digits (0-9), and then with the letters (A – F), depending on the value of y. For example, if y = 12 then the digits are [0,1,… 9, A, B]. Also when y = 3, the possible digits are [0,1,2].
- Since x may contain letters, it’s inputted as a string.
- It’s guaranteed that the number x is a valid number in the base y, and that it doesn’t contain leading zeroes.
- Since the final answer can be very large, output it modulo 1000000007 (10^9+7).
Function Description:
Complete the divisible_k function in the editor below. It has the following parameter(s):
Parameters:
| Name | Type | Description |
|---|---|---|
| y | Integer | the base which x is written in |
| k | Integer | the number which bob has |
| x | String | Alice number written in the base y |
Return: The function must return an INTEGER denoting the number of permutations of x which result in a number divisible by k.
Constraints:
- 1 <= y <= 16
- 1 <= k <= 20
- 1 <= len(x) <= y
Input Format for custom testing:
- The first line contains an integer, y, denoting the base which x is written in.
- The next line contains an integer, k, denoting the number which Bob has.
- The next line contains a string, x, denoting Alice’s number written in the base y.
Sample Cases:
- Sample Input 1
5
4
24 - Sample Output 1
0 - Explanation
24 in base 5, is 14 in decimal. 42 in base 5, is 22 in decimal. For in both cases the number is not divisible by 4. So the answer is 0
Run#include<bits/stdc++.h> using namespace std; int main() { int y,k,m,ans=0; string s; cin>>y>>k>>s; sort(s.begin(),s.end()); m=stoull(s,0,y); if(m%k==0) ans++; while(next_permutation(s.begin(),s.end())) { m=stoull(s,0,y); if(m%k==0) ans++; } cout<<ans; }
from itertools import permutations y=int(input()) k=int(input()) s=input() ans=0 p=permutations(s) L=set(p) pp=list(L) for i in list(pp): a=''.join(i) aa=int(a,y) if aa%k==0: ans+=1 print(ans)
Question 6: Four in a line
Problem Statement -: Given a m x n matrix inmatrix of positive integers, print an integer outnum based on the below logic:
- Identify all possible sets in inmatrix that contain at least four consecutive elements of the same value val, either horizontally, vertically, or diagonally
- If only one set of consecutive elements is identified, store the value val in outnum
- If more than one set of consecutive elements is identified, find the smallest value and store it in outnum
- If no set of four consecutive elements of the same value is identified either horizontally, vertically, or diagonally, print -1
Assumption:
- m and n will be greater than 3
Input format:
- First line will contain number of rows m of inmatrix
- The next m lines will contain the elements of inmatrix. Each line will have n elements separated by space.
- Read the input from the standard input stream.
Output format:
- Print outnum to the standard output stream.
- Sample Input 1
5
0 1 6 8 8 9
5 6 1 6 8 9
6 5 6 1 1 9
1 6 6 1 1 9
6 3 3 3 3 9 - Sample Output 1
1 - Explanation 1
Following elements are present consecutively at least four times: Element 3 horizontally in the 5th row. Element 1 diagonally starting from the 2nd column in the first row. Element 6 diagonally starting from the 4th column in the second row. Element 9 vertically in the 6th column. As element 1 is the smallest value of the four identified sets of consecutive values, the output is 1
- Sample input 2
5
0 1 6 8 6 0
5 5 2 1 8 2
6 5 6 1 1 9
1 5 6 1 4 0
3 7 3 3 4 0 - Sample Output 2
-1 - Explanation 2
Here there are no sets of four consecutive elements of the same value either horizontally, vertically,or diagonally hence output is -1
#include<bits/stdc++.h>
using namespace std;
int main()
{
int m,ans=INT_MAX,I=-1,J=-1;
cin>>m;
vector<vector> mat(m,vector());
cin.ignore();
for(int i=0;i<m;i++)
{
string s;
getline(cin,s);
istringstream ss(s);
while(ss)
{
string w;
ss>>w;
if(w=="") break;
mat[i].push_back(stoi(w));
}
}
int n=mat[0].size();
vector<vector> Ans1(m,vector(n,1));
vector<vector> Ans2(m,vector(n,1));
vector<vector> Ans3(m,vector(n,1));
vector<vector> Ans4(m,vector(n,1));
for(int i=0;i<m-1;i++)
for(int j=0;j<mat[i].size();j++)
if(mat[i][j]==mat[i+1][j])
Ans1[i+1][j]=Ans1[i][j]+1;
for(int i=0;i<m;i++)
for(int j=0;j<mat[i].size() -1;j++)
if(mat[i][j]==mat[i][j+1])
Ans2[i][j+1]=Ans2[i][j]+1;
for(int i=0;i<m-1;i++)
for(int j=0;j<mat[i].size()-1;j++)
if(mat[i][j]==mat[i+1][j+1])
Ans3[i+1][j+1]=Ans3[i][j]+1;
for(int i=0;i<m-1;i++)
for(int j=1;j<mat[i].size();j++)
if(mat[i][j]==mat[i+1][j-1])
Ans4[i+1][j-1]=Ans4[i][j]+1;
for(int i=0;i<m;i++)
for(int j=0;j<mat[i].size();j++)
{
if(Ans1[i][j]>=4 && ans>mat[i][j])
{ans=mat[i][j];I=i;J=j;}
if(Ans2[i][j]>=4 && ans>mat[i][j])
{ans=mat[i][j];I=i;J=j;}
if(Ans3[i][j]>=4 && ans>mat[i][j])
{ans=mat[i][j];I=i;J=j;}
if(Ans3[i][j]>=4 && ans>mat[i][j])
{ans=mat[i][j];I=i;J=j;}
}
if(I==-1)cout<<-1;
else cout<<ans<<endl;
}r=int(input()) a=[] for i in range(r): b=list(map(int,input().split())) a.append(b) c=len(a[0]) ans=set() i=0 while i<r: j=0 while j<(c-3): if a[i][j]==a[i][j+1] and a[i][j]==a[i][j+2] and a[i][j]==a[i][j+3]: ans.add(a[i][j]) j+=4 else: j+=1 i+=1 j=0 while j<c: i=0 while i<(r-3): if a[i][j]==a[i+1][j] and a[i][j]==a[i+2][j] and a[i][j]==a[i+3][j]: ans.add(a[i][j]) i+=4 else: i+=1 j+=1 for i in range(r): i1=i j=0 while (i1+3) if a[i1][j]==a[i1+1][j+1] and a[i1][j]==a[i1+2][j+2] and a[i1][j]==a[i1+3][j+3]: i1+=4 j+=4 ans.add(a[i1][j]) else: i1+=1 j+=1 for j1 in range(1,c): j=j1 i1=0 while (i1+3) if a[i1][j]==a[i1+1][j+1] and a[i1][j]==a[i1+2][j+2] and a[i1][j]==a[i1+3][j+3]: ans.add(a[i1][j]) i1+=4 j+=4 else: i1+=1 j+=1 for i in range(r): i1=i j=(c-1) while (i1+3)=0: if a[i1][j]==a[i1+1][j-1] and a[i1][j]==a[i1+2][j-2] and a[i1][j]==a[i1+3][j-3]: i1+=4 j-=4 ans.add(a[i1][j]) else: i1+=1 j-=1 for j1 in range(c-2,-1,-1): j=j1 i1=0 while (i1+3)=0: if a[i1][j]==a[i1+1][j-1] and a[i1][j]==a[i1+2][j-2] and a[i1][j]==a[i1+3][j-3]: ans.add(a[i1][j]) i1+=4 j-=4 else: i1+=1 j-=1 if len(ans)>=1: print(min(ans)) else: print(-1)
Question 7 : Identify Palindrome
Problem Statement-: For a given positive number num, identify the palindrome formed by performing the following operations-
- Add num and its reverse
- Check whether the sum is palindrome or not. If not, add the sum and its reverse and repeat the process until a palindrome is obtained
For example:
If original integer is 195, we get 9,339 as the resulting palindrome after the fourth addition:
195
+ 591
————–
786
+ 687
————–
1473
+ 3741
————–
5214
+ 4125
———-
9339
Input format:
- Read num from the standard input stream.
Output format:
- Print the palindrome calculated to the standard output stream.
Sample Test Cases
- Sample Input 1
124 - Sample Output 1
545 - Explanation 1
The sum of 124 and its reverse 421 is 545 which is a palindrome.
- Sample input 1
4 - Sample output 1
8 - Explanation 1
The sum of 4 and its reverse 4 is 8 which is a palindrome.
#include <bits/stdc++.h>
using namespace std;
string Add(string s1,string s2)
{
int i=stoi(s1)+stoi(s2);
return to_string(i);
}
string rev(string s)
{
reverse(s.begin(),s.end());
return s;
}
bool Palindrome(string s1)
{
return s1==rev(s1);
}
int main()
{
string s;
cin>>s;
while(1)
{
string s1=Add(s,rev(s));
//cout<<s1<<endl;
if(Palindrome(s1)){cout<<s1;return 0;}
s=s1;
}
}
def isPalindrome(n):
return str(n)[::-1]==str(n)
def rev(n):
return int(str(n)[::-1])
n=int(input())
while(1):
n=n+rev(n)
if(isPalindrome(n)):
print(n)
break
import java.util.Objects;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
Integer num = scanner.nextInt();
while (true) {
Integer addedNum = num + reverse(num);
if (Objects.equals(addedNum, reverse(addedNum))){
System.out.println( addedNum);
break;
}
num = addedNum;
}
}
private static Integer reverse(Integer number) {
int reverse = 0;
while (number != 0) {
int remainder = number % 10;
reverse = reverse * 10 + remainder;
number = number / 10;
}
return reverse;
}
}Question 8: Minimum Withdrawals
Problem Statement-: There is a unique ATM in Wonderland. Imagine this ATM as an array of numbers. You can withdraw cash only from either ends of the array. Sarah wants to withdraw X amount of cash from the ATM. What is the minimum number of withdrawals Sarah would need to accumulate X amount of cash. If it is not possible for Sarah to withdraw X amount, return -1.
Input Format
- The first line contains an integer, N, denoting the number of elements in ATM.
- Each line i of the N subsequent lines (where 0 <= i < N) contains an integer describing the cash in the ATM.
- The next line contains an integer, X, denoting the total amount to withdraw.
Constraints
- 1 <= N <= 10^5
- 1 <= ATM [i] <= 10^5
- 1 <= X <= 10^5
Sample Test Cases
- Sample Input
2
1
1
3 - Sample Output
-1 - Explanation
The total amount of cash in the ATM is 2, hence Sarah cannot withdraw an amount of 3.
>#include <bits/stdc++.h>
using namespace std;
int l;
int fun(int s,int e,int k,vector a)
{
if(k==0) return 0;
if(s>e || k<0) return l;
return min(1+fun(s+1,e,k-a[s],a),1+fun(s,e-1,k-a[e],a));
}
int main()
{
int n;cin>>n;
vector a(n);
for(int i=0;i<n;i++) cin>>a[i];
l=pow(10,9);
int k;cin>>k;
int kk=fun(0,n-1,k,a);
if(kk>=l){cout<<-1;}
else cout<<kk;
}n=int(input()) a=[] for i in range(n): a.append(int(input())) def answer(s,e,k): if k==0: return 0 if s>e or k<0: return 10**9 else: return min(1+answer(s+1,e,k-a[s]),1+answer(s,e-1,k-a[e])) k=int(input()) k1=answer(0,n-1,k) if k1>=(10**9): print(-1) else: print(k1)
import java.util.*;
import java.lang.Math;
class Main {
static int l;
static int fun(int s, int e, int k, int a[]) {
if (k == 0) return 0;
if (s > e || k < 0) return l;
return Math.min(1 + fun(s + 1, e, k - a[s], a), 1 + fun(s, e - 1, k - a[e], a));
}
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
int n;
n = sc.nextInt();
int v[] = new int[n];
for (int i = 0; i < n; i++) {
v[i] = sc.nextInt();
}
l = (int) Math.pow(10, 9);
int k;
k = sc.nextInt();
int kk = fun(0, n - 1, k, v);
if (kk >= l) {
System.out.println("-1");
} else System.out.println(kk);
}
}Question 9: Team Division
Problem Statement -: Consider an array inarr containing at least two non-zero positive integers ranging between 1 to 300 (inclusive of the boundary values). Divide the integers in inarr into two groups based on the below rules:
- Each of the integers should belong to either of the two groups
- The total sum of integers in each of the groups must be as nearly equal as possible
- The total number of integers between the two groups should not differ by more than 1
Print, outnum1 and outnum2, the sum of the integers of two groups separated by a space. If outnum1 and outnum2 are not equal, then print the smaller sum followed by the larger sum.
Input Format:
- Read the array inarr elements separated by (‘,’) comma.
- Read the input from the standard input stream.
Output Format:
- Print outnum1 and outnum2 in the required order separated by a space.
- Print the output to the standard output stream.
Sample Test Cases
- Sample Input
87,100,28,67,68,41,67,1 - Sample Output
229 230
Explanation
For the given input, the two groups that can be formed following the mentioned rules are:
- Group 1: 87 100 41 1
- Group 2: 28 67 68 67
The total sum of integers in each of the groups which is as nearly equal as possible is:
- Group 1-Total Sum:229
- Group 2-Total Sum:230
The total number of integers between group 1 and 2 differ by O integer.
#include<bits/stdc++.h>
using namespace std;
vector v;
int ans(int i,int n,float s)
{
if(i<n-1) return INT_MAX;
if(n==0) return abs(s);
return min(ans(i-1,n-1,s-v[i-1]),ans(i-1,n,s));
}
int main()
{
string s;
cin>>s;
int c=0;
for(int i=0;i<s.length();i++)
{
if(s[i]==',') {v.push_back(stoi(s.substr(c,i-c)));
c=i+1;}
}
v.push_back(stoi(s.substr(c,s.length()-c)));
//for(int i=0;i<v.size();i++) cout<<v[i];
int ss=0;
for(int i=0;i<v.size();i++) ss+=v[i];
int n1=v.size();
int n2=n1/2;
float su=ss/2;
int k=ans(n1-1,n2,su);
cout<<ss-su-k<<" "<<su+k;
}
a=list(map(int,input().split(',')))
n1=len(a)
n2=n1//2
su=sum(a)/2
dp=[[-1 for i in range(n2+1)] for j in range(n1)]
def answer(i,n,s):
if i<(n-1):
return float('inf')
if n==0:
return abs(s)
else:
return min(answer(i-1,n-1,s-a[i-1]),answer(i-1,n,s))
k=answer(n1-1,n2,su)
print(int(su-k),int(su+k))
Question 10: Mark’s Game
Problem Statement-: Mark is playing a game on a 2D map. The 2D map is a rectangle of size n*m, where n is the number of rows, and m is the number of columns. The cell (1,1) is located at the top left corner of the map, and the cell (n,m) is located at the bottom right corner.
In one step, Mark can move from any cell to any of the adjacent cells (UP, DOWN, RIGHT, or LEFT). There’s also a blocked cell (x,y) which Mark can’t pass on. Mark can’t go off the map.
The goal of the game is to reach the cell (n,m). Mark is initially at cell (1,1) and he wants to achieve the goal of the game in the minimum number of steps. Now he’s wondering how many paths he can take such that the number of steps is minimized and he gets to cell (n,m). Can you help him find this number?
It is guaranteed that both cells (1,1) and (n,m) are NOT blocked.
Function Description:
- Complete the markgame function in the editor below. It has the following parameter(s):
Parameters:
| Name | Type | Description |
|---|---|---|
| n | Integer | The number of rows in the map. |
| m | Integer | The number of columns in the map. |
| x | Integer | The blocked cell’s row. |
| y | Integer | The blocked cell’s column. |
Constraints:
- 1 <= n <= 10^2
- 1 <= m <= 10^2
- 1 <= x <= n
- 1 <= y <= m
Input Format:
- The first line contains an integer, n, denoting the number of rows in the map.
- The next line contains an integer m, denoting the number of columns in the map.
- The next line contains an integer, x, denoting the blocked cell’s row.
- The next line contains an integer, y, denoting the blocked cell’s column.
Sample Test Cases
- Sample Input 1
2
2
2
1 - Sample Output 1
1
#include <bits/stdc++.h>
using namespace std;
unordered_map<int,long long int> f;
long long int Fact(int n)
{
if(f[n]) return f[n];
return f[n]=n*Fact(n-1);
}
int main()
{
int n,m,x,y;
cin>>n>>m>>x>>y;
n-=1;m-=1;x-=1;y-=1;
f[0]=f[1]=1;
int p=(Fact(m+n)/(Fact(m)*Fact(n)));
int imp=((Fact(x+y)/(Fact(x)*Fact(y)))*(Fact(m-x+n-y)/(Fact(m-x)*Fact(n-y))));
cout<<p-imp;
}import math n=int(input())-1 m=int(input())-1 x=int(input())-1 y=int(input())-1 ans=math.factorial(n+m) ans=ans//(math.factorial(n)) ans=ans//(math.factorial(m)) ans1=math.factorial(x+y) ans1=ans1//(math.factorial(x)) ans1=ans1//(math.factorial(y)) x1=n-x y1=m-y ans2=math.factorial(x1+y1) ans2=ans2//(math.factorial(x1)) ans2=ans2//(math.factorial(y1)) print(ans-(ans1*ans2))
import java.util.*;
class Main
{
static int f[] = new int[1000];
static int Fact(int n)
{
if(f[n]==1) return f[n];
return f[n]=n*Fact(n-1);
}
public static void main (String[]args)
{
Scanner sc = new Scanner (System.in);
int n = sc.nextInt ();
int m = sc.nextInt ();
int x = sc.nextInt ();
int y = sc.nextInt ();
n-=1;m-=1;x-=1;y-=1;
f[0]=f[1]=1;
int p=(Fact(m+n)/(Fact(m)*Fact(n)));
int imp=((Fact(x+y)/(Fact(x)*Fact(y)))*(Fact(m-x+n-y)/(Fact(m-x)*Fact(n-y))));
System.out.println(p-imp);
}
}Question 11 : Santa and Gifts
Problem statement-: Christmas is here! Santa has already prepared the gifts for all children all around the world, however, he hasn’t picked them yet. Santa has N gifts, their sizes are given in an array, A, and he also has N boxes, their sizes are given in an array, B.
Santa packs the gifts in the boxes in the following way:
- He tries to put the gifts inside boxes from left to right.
- He goes through the boxes from left to right until he finds the first empty box that fits the current gift (the box’s size should be larger or equal to the current gift’s size), and Santa puts the current gift in that box.
- Santa moves to the next gift to the right.
You need to find the number of gifts which won’t be packed following Santa’s algorithms in packing the gifts.
Function Description:
- Complete the santa function in the editor below. It has the following parameter(s):
Parameters:
| Name | Type | Description |
| n | Integer | The number of gifts and boxes |
| a | Integer array | The size of gifts |
| b | Integer array | The size of the boxes |
Return:
The function must return an INTEGER denoting the number of gifts which won’t be packed.
Constraints:
- 1 <= N <= 10^3
- 1 <= A[i] <= 10^5
- 1 <= B[i] <= 10^5
Input Format for Custom Testing:
- The first line contains an integer, N, denoting the number of elements in A.
- Each line i of the N subsequent lines (where 0 <= i <= N) contains an integer describing Ai.
- Each line i of the N subsequent lines (where 0 <= i <= N) contains an integer describing Bi.
Sample Test Cases
- Sample Input 1
2
4
5
10
4 - Sample Output 1
1
#include <bits/stdc++.h>
using namespace std;
string Add(string s1,string s2)
{
int i=stoi(s1)+stoi(s2);
return to_string(i);
}
string rev(string s)
{
reverse(s.begin(),s.end());
return s;
}
bool Palindrome(string s1)
{
return s1==rev(s1);
}
int main()
{
int n; cin>>n;
vector p(n),h(n);
for(int i=0;i<n;i++) cin>>p[i];
for(int i=0;i<n;i++) cin>>h[i];
int c=0;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
if(p[i]>h[j])
{
c++;h[j]-=1;break;
}
cout<<n-c;
}
N=int(input())
people=[]
house=[]
#to read data of people and house arrays
for i in range(N): people.append(int(input()))
for i in range(N): house.append(int(input()))
count=0
for i in range(N):
for j in range(N):
if(people[i]<house[j]):
count+=1
house[j]=-1
break
print(N-count)
import java.util.*;
class Main {
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
int n;
n = sc.nextInt();
int p[] = new int[n];
int h[] = new int[n];
for (int i = 0; i < n; i++) {
p[i] = sc.nextInt();
}
for (int i = 0; i < n; i++) {
h[i] = sc.nextInt();
}
int c = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (p[i] > h[j]) {
c++;
h[j] -= 1;
break;
}
}
}
System.out.println(n - c);
}
}
 Apply For Jobs
Apply For Jobs Get Hiring Updates
Get Hiring Updates


Login/Signup to comment