Majority Element in an Array in Java

August 8, 2025

Majority Element in an Array in Java

In algorithm design and data analysis, the concept of a “Majority element in an array in java” holds special significance. It refers to an element that appears more than half the time in a given array.

Identifying such an element is not only a classic algorithmic challenge but also a practical problem with real world applications in fields like voting systems, data stream processing, and distributed computing.

This article explores the different approaches to solving the Majority Element problem in Java, from naive brute force methods to highly optimized algorithms like the Boyer Moore Voting Algorithm.

Majority Element in Array In Java

Majority Element In An Array In Java

  1. This problem is a common algorithmic question in coding interviews and has several solutions with varying time and space complexities.
  2. Identifying the majority element is not just a theoretical exercise; it has real world relevance in various domains such as data streams, voting systems, distributed computing, and consensus mechanisms.

For instance, in elections, the candidate with more than half the votes is the winner.

In distributed systems, determining a majority node agreement is crucial for fault tolerant decision making.

Problem Statement

Given an array of size n, find the element that appears more than n/2 times. 

If such an element exists, return it. Otherwise, return -1.

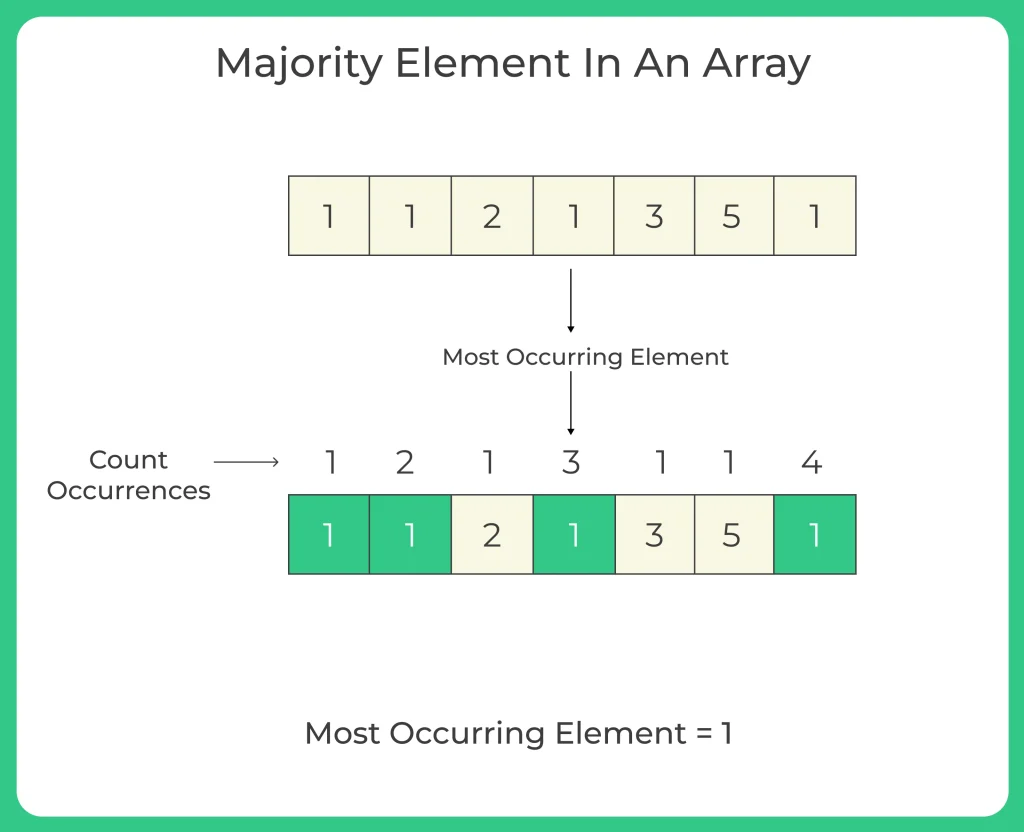
Majority Element In An Array
DSA desktop gif
DSA mobile gif

Introduction  to Arrays

Introduction to 2-D Arrays

Array Rotation

Reverse an Array or String

Sort the array in Waveform

Methods to Find Majority Element in an Array

1. Brute Force Approach

Algorithm:

  • For every element, count its frequency by scanning the entire array.
  • If frequency > n/2, return the element.

Code:

Run

public class MajorityElementBruteForce {
    public static int findMajority(int[] nums) {
        int n = nums.length;
        for (int i = 0; i < n; i++) {
            int count = 0;
            for (int j = 0; j < n; j++) { if (nums[j] == nums[i]) count++; } if (count > n / 2) return nums[i];
        }
        return -1;
    }

    public static void main(String[] args) {
        int[] nums = {2, 2, 1, 2, 3, 2, 2};
        System.out.println("Majority Element: " + findMajority(nums));
    }
}

Output:

Majority Element: 2

2. Hash Map Counting Approach

Algorithm:

  • Use a HashMap to count the frequency of each element.
  • Return the element with count > n/2.

Code:

Run 
import java.util.HashMap;

public class MajorityElementHashMap {
    public static int findMajority(int[] nums) {
        HashMap map = new HashMap<>();
        int n = nums.length;
        for (int num : nums) {
            map.put(num, map.getOrDefault(num, 0) + 1);
            if (map.get(num) > n / 2) return num;
        }
        return -1;
    }

    public static void main(String[] args) {
        int[] nums = {3, 3, 4, 2, 3, 3, 3};
        System.out.println("Majority Element: " + findMajority(nums));
    }
}
Output: 
Majority Element: 3

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Majority Element In An Array In Java Programming

3. Sorting Approach For Majority Element in an Array

Algorithm:

  • Sort the array.
  • The element at the middle (n/2 index) is guaranteed to be the majority if it exists.

Code:

Run 
import java.util.Arrays;

public class MajorityElementSorting {
    public static int findMajority(int[] nums) {
        Arrays.sort(nums);
        return nums[nums.length / 2];
    }

    public static void main(String[] args) {
        int[] nums = {1, 1, 2, 1, 3, 1, 1};
        System.out.println("Majority Element: " + findMajority(nums));
    }
}
Output: 
Majority Element: 1

4. Boyer Moore Voting Algorithm For Majority Element

Algorithm:

  1. Initialize candidate and count = 0.
  2. For each element:
  • If count == 0, set candidate to current element.
  • If element == candidate, increment count.
  • Else, decrement count.

This algorithm is an elegant and efficient way to find a majority element in linear time and constant space.

Idea is to cancel out each occurrence of an element with a different element. Since the majority element appears more than half the time, it will remain as the last candidate.

  1. Mathematically, the algorithm works by maintaining a balance counter.
  2. The count is increased when the same element appears and decreased when a different one appears.
  3. This simulates a voting process where every non majority element votes against the current candidate.

When the count drops to zero, we assume the previous candidate is outvoted and reset the candidate.

Code:

Run 
public class MajorityElementBoyerMoore {
    public static int findMajority(int[] nums) {
        int candidate = 0, count = 0;
        for (int num : nums) {
            if (count == 0) {
                candidate = num;
            }
            count += (num == candidate) ? 1 : -1;
        }
        return isValidMajority(nums, candidate) ? candidate : -1;
    }

    private static boolean isValidMajority(int[] nums, int candidate) {
        int count = 0;
        for (int num : nums) {
            if (num == candidate) count++;
        }
        return count > nums.length / 2;
    }

    public static void main(String[] args) {
        int[] nums = {2, 2, 1, 1, 1, 2, 2};
        System.out.println("Majority Element: " + findMajority(nums));
    }
}
Output: 
Majority Element: 2

Using a Simple Linked List to Store Input

Linked lists offer dynamic memory allocation and are ideal for situations where the size of the input is unknown at compile time. They also provide a useful abstraction in teaching basic data structure operations.

Code:

Run

class Node {
    int data;
    Node next;

    Node(int data) {
        this.data = data;
        this.next = null;
    }
}

class SimpleLinkedList {
    Node head;

    void add(int data) {
        if (head == null) {
            head = new Node(data);
            return;
        }
        Node current = head;
        while (current.next != null) {
            current = current.next;
        }
        current.next = new Node(data);
    }

    int[] toArray() {
        int size = 0;
        Node temp = head;
        while (temp != null) {
            size++;
            temp = temp.next;
        }
        int[] array = new int[size];
        temp = head;
        for (int i = 0; i < size; i++) {
            array[i] = temp.data;
            temp = temp.next;
        }
        return array;
    }
}

Integration with Majority Element

public class MajorityElementWithLinkedList {
    public static void main(String[] args) {
        SimpleLinkedList list = new SimpleLinkedList();
        list.add(1);
        list.add(2);
        list.add(1);
        list.add(1);
        list.add(3);
        list.add(1);
        list.add(1);

        int[] array = list.toArray();
        int majority = MajorityElementBoyerMoore.findMajority(array);
        System.out.println("Majority Element: " + majority);
    }
}

Output:

Majority Element: 1

Conclusion

The Majority Element problem can be solved using several techniques, each with trade offs:

  1. Brute Force: Simple but inefficient; use only for small datasets.
  2. HashMap: Fast but uses extra space; suitable when space isn’t constrained.
  3. Sorting: Cleaner and moderate in performance; use when sorting doesn’t add overhead.
  4. Boyer Moore: Best for performance and space; ideal for large arrays or streaming data.

When designing a solution, consider input size, space limitations, and performance requirements.

Understanding these trade offs is crucial for writing efficient and scalable algorithms.

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout

Arrays

  • Introduction to Arrays – C | C++ | Java
  • Introduction to 2-D Arrays – C | C++ | Java
  • Sorting of Array – C | C++ | Java
  • Array Rotation – C | C++ | Java
  • Reverse an array or string- C | C++ | Java
  • Find pairs in array with given sum – C | C++ | Java
  • Sort the array in Waveform – C | C++ | Java
  • Majority Element in Array – C | C++ | Java
  • Boyer-Moore’s Voting Algorithm – C | C++ | Java
  • K-pairs with smallest sum in 2 arrays – C | C++ | Java
  • Largest Sum Contigous SubArray – C | C++ | Java
  • Maximum Average Sub-array of K length – C | C++ | Java
  • Size of sub-array with max sum – C | C++ | Java
  • Sub-array with given sum – C | C++ | Java
  • Triplet that sum to a given value – C | C++ | Java
  • Segregate 0’s and 1’s in array – C | C++ | Java
  • Segregate 0’s 1’s and 2’s in array – C | C++ | Java
  • Sort elements in array by frequency – C | C++ | Java
  • Finding pythagorean triplets in an array – C | C++ | Java
  • Reorder array using given indexes – C | C++ | Java
  • Merging two sorted arrays – C | C++ | Java
  • Minimum number of Merge Operations to make an Array Palindrome – C | C++ | Java
  • Find Zeros to be Flipped so that number of Consecutive 1’s is maximized – C | C++ | Java