0
Notifications Mark All Read
- Login
- Get Prime
Reorder Array using Given Indexes in Java
Reorder Array Using Given Indexes
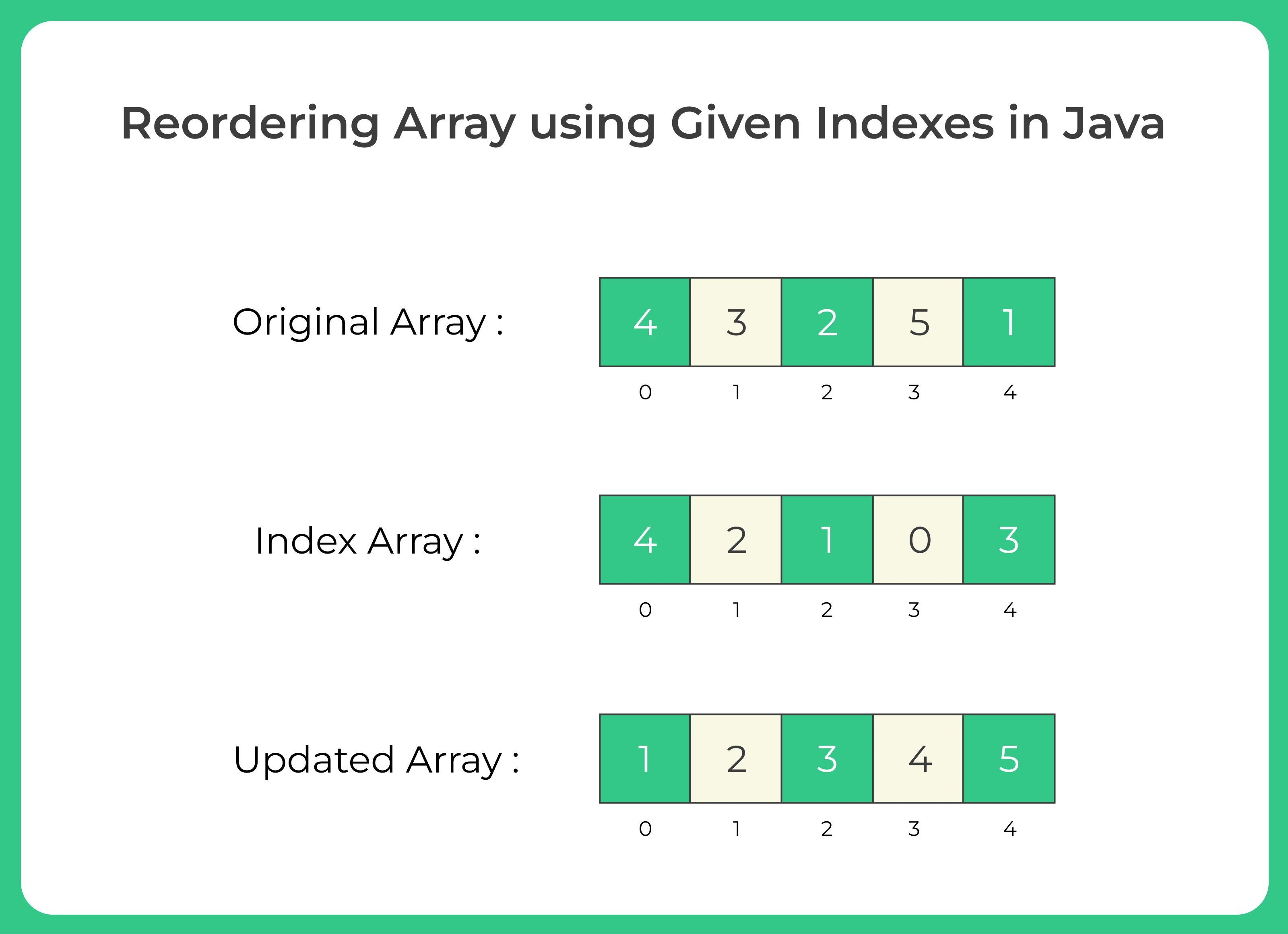
On this page we will discuss about reorder array using given indexes . Given two input arrays of same size, second array is index array, we need to reorder array using given indexes array.
Reorder Array Using Given Indexes in Java language
In computer science, reordering an array using given indexes is a common problem. Given an array of values and an array of indexes, the task is to reorder the values in the array based on the given indexes.
The basic idea behind this problem is to create a temporary array to hold the sorted values and then copy the sorted values back into the original array in the correct order.
To do this, we first declare the two arrays: the array containing the values to be sorted, and the array containing the indexes that specify the order in which the values should be sorted.
Next, we create a temporary array to hold the sorted values. We then loop through the index array and assign the values from the original array to the temporary array in the correct order specified by the index array.
Finally, we copy the values from the temporary array back into the original array, effectively reordering the array according to the specified indexes.
Algorithm :
- Take the size of the array from the user and store it in variable n.
- Declare two arrays arr[] and idx[], one for array elements and another to store the require indexes value.
- Take the elements of the both arrays from the user.
- Declare an another array for the output say, res[].
- Traverse the result array and set, res[idx[i]]=arr[].
Code in Java For Reorder Array Using Given Indexes
public class Main {
public static void main(String[] args) {
int[] arr = {10, 20, 30, 40, 50};
int[] index = {3, 1, 4, 0, 2};
int[] temp = new int[5];
for (int i = 0; i < 5; i++) {
temp[i] = arr[index[i]];
}
for (int i = 0; i < 5; i++) {
arr[i] = temp[i];
}
System.out.print("Reordered array: ");
for (int i = 0; i < 5; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
}
Output
Reordered array: 40 20 50 10 30
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java

 0
0



Login/Signup to comment