Largest Sum Contiguous SubArray

February 2, 2021

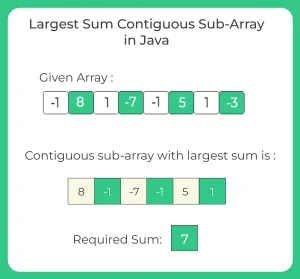
Largest Sum Contiguous SubArray in Java

Problem Statement:

Given an integer array nums find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

Input:

nums = [-2,1,-3,4,-1,2,1,-5,4]

Output: 6

Explanation: [4,-1,2,1] has the largest sum = 6.

Algorithm:

Start
Maxsofar = array[0] curr_Max = tempMax
for i = 1 to n,
do
currMax = maximum of (array[i] and currentMax+array[i])
Maxsofar = maximum of (curr_Max and Maxsofar)
done
return Maxsofar
End

Java code :

// Java program to print largest contiguous 
// array sum 
import java.io.*; 

class prepinsta { 

    static int maxSubArraySum(int a[], int n) 
    { 
    int maxsofar = a[0]; 
    int curr_max = a[0]; 

    for (int i = 1; i < n; i++) 
    { 
        curr_max = Math.max(a[i], curr_max+a[i]); 
        maxsofar = Math.max(maxsofar, curr_max); 
    } 
    return maxsofar; 
    } 

    /* Driver program to test maxSubArraySum */
    public static void main(String[] args) 
    { 
    int a[] = {-2,1,-3,4,-1,2,1,-5,4}; 
    int n = a.length; 
    int max_sum = maxSubArraySum(a, n); 
    System.out.println(“Maximum contiguous sum is “
                    + max_sum); 
    } 
} 

Output :

Maximum contiguous sum is 6