Merge Sort in Java
Merge Sort in Java Programming
In this article, we will learn about Merge Sort in Java. We will explain how it works, walk through the algorithm step by step, show its implementation in Java, and discuss its time and space complexity. Sorting is a key concept in computer science that helps arrange data efficiently.

What is Merge Sort?
How Merge Sort Works ?
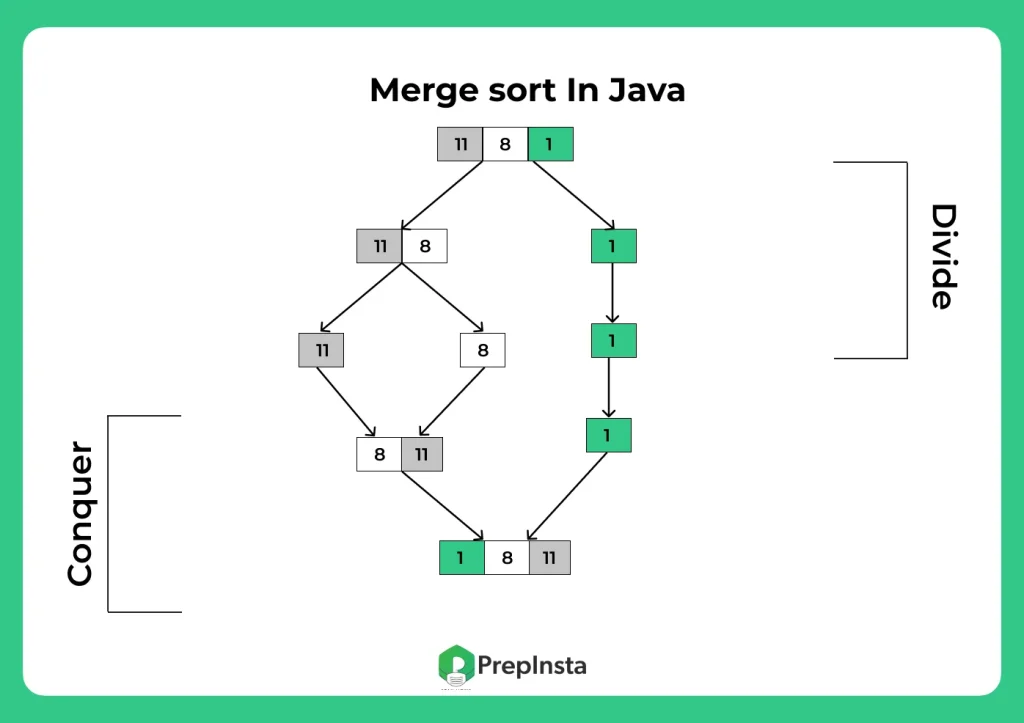
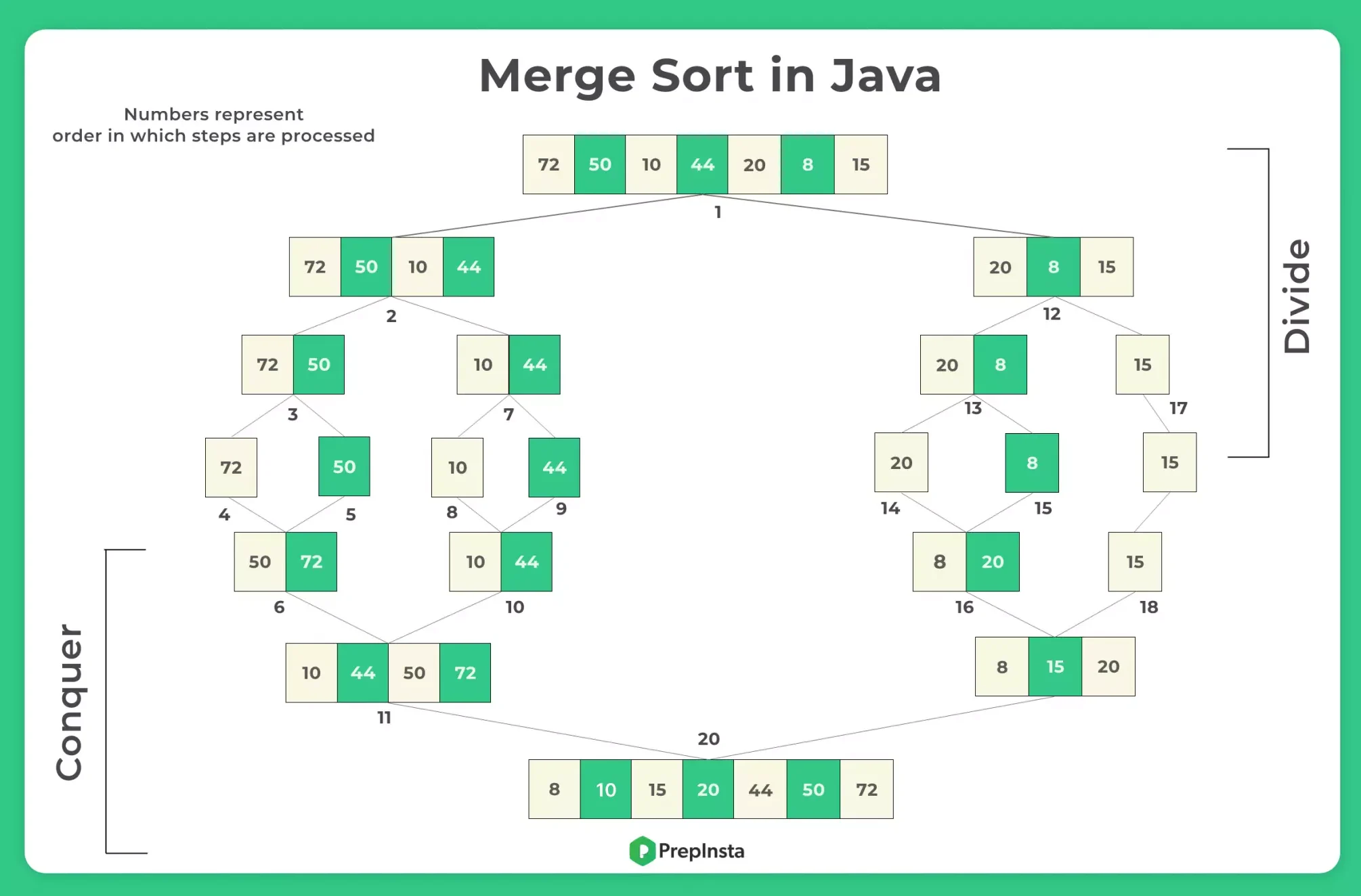
Merge Sort works in three main steps:
- Divide: Split the array into two halves recursively.
- Conquer: Sort each half recursively.
- Merge: Combine the sorted halves into one sorted array.
Recursion continues until each subarray has only one element. Then, it merges the sorted parts one by one.
Algorithm of Merge Sort
Here’s a step by step breakdown of the Merge Sort algorithm:
1. If the array has more than one element:
- Find the middle index of the array.
- Divide the array into two halves: left and right.
- Recursively call Merge Sort on both halves.
- Merge the sorted halves.
2. If the array has only one element, it is already sorted.
Pseudocode:
mergeSort(arr, left, right)
if left < right
mid = (left + right) / 2
mergeSort(arr, left, mid)
mergeSort(arr, mid + 1, right)
merge(arr, left, mid, right)

Learn DSA
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Implementation of Merge Sort in Java Programming
Code:
public class MergeSort {
// Function to sort the array using merge sort
public void mergeSort(int[] arr, int left, int right) {
if (left < right) {
// Find the middle point
int mid = left + (right - left) / 2;
// Sort first and second halves
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
// Merge the sorted halves
merge(arr, left, mid, right);
}
}
// Function to merge two subarrays of arr[]
public void merge(int[] arr, int left, int mid, int right) {
// Find sizes of two subarrays to be merged
int n1 = mid - left + 1;
int n2 = right - mid;
// Create temp arrays
int[] leftArray = new int[n1];
int[] rightArray = new int[n2];
// Copy data to temp arrays
for (int i = 0; i < n1; i++)
leftArray[i] = arr[left + i];
for (int j = 0; j < n2; j++)
rightArray[j] = arr[mid + 1 + j];
// Merge the temp arrays
int i = 0, j = 0;
int k = left;
while (i < n1 && j < n2) {
if (leftArray[i] <= rightArray[j]) {
arr[k] = leftArray[i];
i++;
} else {
arr[k] = rightArray[j];
j++;
}
k++;
}
// Copy remaining elements of leftArray
while (i < n1) {
arr[k] = leftArray[i];
i++;
k++;
}
// Copy remaining elements of rightArray
while (j < n2) {
arr[k] = rightArray[j];
j++;
k++;
}
}
// Utility method to print the array
public void printArray(int[] arr) {
for (int value : arr)
System.out.print(value + " ");
System.out.println();
}
// Main method to test the algorithm
public static void main(String[] args) {
MergeSort ms = new MergeSort();
int[] arr = { 12, 11, 13, 5, 6, 7 };
System.out.println("Original array:");
ms.printArray(arr);
ms.mergeSort(arr, 0, arr.length - 1);
System.out.println("Sorted array:");
ms.printArray(arr);
}
}
Explanation of the Merge Sort Code:
- mergeSort() – This is the main recursive method. It splits the array and calls itself on both halves.
- merge() – This method merges two sorted sub arrays. It uses temporary arrays to store elements during merging.
- printArray() – A utility function to display the array.
- main() – This method sets up an example array, applies merge sort, and prints the results.
Average Case: O(n log n)
Worst Case: O(n log n)

Program for Merge Sort in Java using Multiple Arrays
In Java, there are two common ways to implement the Merge Sort algorithm.
Both methods follow the same core logic of divide and conquer, but they differ slightly in how they handle the arrays during the merging process:
- Method 1: Using Two Separate Subarrays:
- In this method, we create two temporary subarrays, one for the left half and one for the right half of the main array.
- These subarrays are used to hold the elements before merging them back in sorted order. This method makes the merging step clearer and easier to follow, especially for beginners.
- Method 2: Using a Single Array with Index Ranges
- This variation performs the same operations, but instead of creating two separate subarrays, it works with a single array by tracking the start and end indices.
- This helps reduce some overhead in terms of copying data, but the logic can be a bit more complex.
Space complexity is the same i.e. O(n) in both cases as even though there are two subarrays in method 1 they in total have n array items and method 2 also with one single array also has n array items.
//Java Program for Merge Sort
class Main {
// this function display the array
public static void display(int[] arr, int size)
{
for(int i = 0; i < size; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
// main function of the program
public static void main(String[] args)
{
int[] a = {12, 8, 4, 14, 36, 64, 15, 72, 67, 84};
int size = a.length;
display(a, size);
mergeSort(a, 0, size - 1);
display(a, size);
}
// this function apply merging and sorting in the array
static void mergeSort(int[] a, int left, int right)
{
int mid;
if(left < right)
{
// can also use mid = left + (right - left) / 2
// this can avoid data type overflow
mid = (left + right) / 2;
// recursive calls to sort first half and second half sub-arrays
mergeSort(a, left, mid);
mergeSort(a, mid + 1, right);
merge(a, left, mid, right);
}
}
// after sorting this function merge the array
static void merge(int[] arr, int left, int mid, int right)
{
int i, j, k;
int n1 = mid - left + 1;
int n2 = right - mid;
// create temp arrays to store left and right sub-arrays
int L[] = new int[n1];
int R[] = new int[n2];
// Copying data to temp arrays L[] and R[]
for (i = 0; i < n1; i++)
L[i] = arr[left + i];
for (j = 0; j < n2; j++)
R[j] = arr[mid + 1 + j];
// here we merge the temp arrays back into arr[l..r]
i = 0; // Starting index of L[i]
j = 0; // Starting index of R[i]
k = left; // Starting index of merged sub-array
while (i < n1 && j < n2)
{
// place the smaller item at arr[k] pos
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
}
else {
arr[k] = R[j];
j++;
}
k++;
}
// Copy the remaining elements of L[], if any
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
// Copy the remaining elements of R[], if any
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
}
Output
12 8 4 14 36 64 15 72 67 84 4 8 12 14 15 36 64 67 72 84
//Java Program for Merge Sort
class Main {
// this function display the array
public static void display(int[] arr, int size)
{
for(int i = 0; i < size; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
// main function of the program
public static void main(String[] args)
{
int[] a = {12, 8, 4, 14, 36, 64, 15, 72, 67, 84};
int size = a.length;
display(a, size);
mergeSort(a, 0, size - 1);
display(a, size);
}
// this function apply merging and sorting in the array
static void mergeSort(int[] a, int left, int right)
{
int mid;
if(left < right)
{
// can also use mid = left + (right - left) / 2
// this can avoid data type overflow
mid = (left + right) / 2;
// recursive calls to sort first half and second half sub-arrays
mergeSort(a, left, mid);
mergeSort(a, mid + 1, right);
merge(a, left, mid, right);
}
}
// after sorting this function merge the array
static void merge(int[] a, int left, int mid, int right)
{
int i = left; // starting index of left sub-array
int j = mid + 1; // starting index of right sub-array
int index = left; // used to place items in temp[]
int[] temp = new int[10];
while(i <= mid && j <= right)
{
// place the smaller item at temp[index]
if(a[i] < a[j]) { temp[index] = a[i]; i = i + 1; } else { temp[index] = a[j]; j = j + 1; } index++; } // i > mid would mean all items for left
// sub-array were successfully placed, and there
// must be unplaced right sub-array items
if(i > mid)
{
while(j <= right) {
temp[index] = a[j];
index++;
j++;
}
}
else {
while(i <= mid)
{
temp[index] = a[i];
index++;
i++;
}
}
int p = left;
while(p < index)
{
a[p] = temp[p];
p++;
}
}
}
Output
12 8 4 14 36 64 15 72 67 84 4 8 12 14 15 36 64 67 72 84
Advantages of Merge Sort
- Stable Sort – It maintains the order of equal elements.
- Predictable Performance – Always runs in O(n log n) time.
- Useful for Linked Lists – Does not require random access.
- Efficient for Large Data – Performs better than bubble or insertion sort on large datasets.
Disadvantages of Merge Sort
- Uses Extra Space – Not ideal for memory constrained systems.
- Slower on Small Data – For small arrays, insertion sort can be faster.
- Complex Implementation – More complex than simple sorting methods.
Conclusion
Merge Sort is a powerful and efficient sorting algorithm based on the divide and conquer principle. Its predictable O(n log n) time complexity makes it a great choice for sorting large arrays and linked lists.
Although it uses extra space, its stability and consistent performance give it an edge over some other algorithms.

FAQ's related to Merge Sort in Java
Answer:
Merge Sort is based on the divide and conquer technique. It splits the array into halves, recursively sorts them, and merges the sorted halves to produce the final sorted array.
Answer:
No, Merge Sort is not in-place. It uses extra space for temporary arrays during the merge process, which leads to a space complexity of O(n).
Answer:
Merge Sort maintains the relative order of equal elements while merging, which makes it stable. This is important when sorting records with multiple fields (like name and age).
Answer:
Merge Sort has a time complexity of O(n log n) in the best, average, and worst cases, making it very predictable and efficient even for large datasets.
Answer:
Merge Sort is preferred when stability is required or when dealing with linked lists. It is also a better choice in worst case scenarios where Quick Sort can degrade to O(n²).
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others




Login/Signup to comment