Bouncing Ball Puzzle
Solve the Bouncing Ball Puzzle
Step-Wise Explanation for Bouncing Ball Puzzle is given here on this page.
If I throw a ball from a 50-storied building, the ball upon hitting the ground bounces back half the way up and goes down and again bounces half the way up.
If this continues, how many bounces will it take before the ball comes to a permanent halt?

- We can say that in the first bounce the ball covers half the height of the building, say x
- Then in the second bounce, it will cover half of the first distance, say x/2
- On the third distance, it will cover half of that distance, say x/4
- And this will continue for the rest of the journey.
- To simplify it further, say the ball bounces at a height of 0.1 cm, in the next step it will bounce to a height of (0.1/2) cm or 0.05cm.
- And then for the next bounce, the ball will bounce (0.05/2)cm or 0.025cm.
- Therefore in essence there will always be some distance(no matter how small) for the ball to cover.
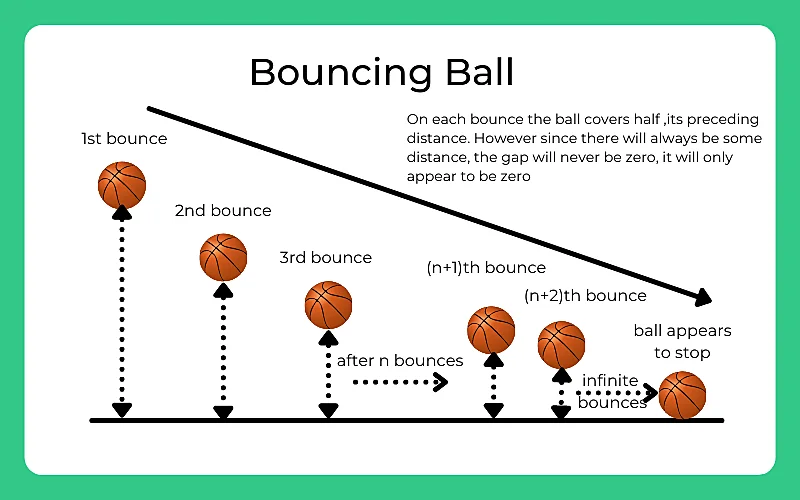
- However, since there is gravitational force at some point it will overpower the ball’s inertia and cause it to stop.
- But the number of bounces it will take is infinite.
Note:- This puzzle follows the Greek philosopher Zeno’s dichotomy paradox.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others






Login/Signup to comment