Binary Search in Java

March 18, 2022

Binary Search in JAVA

Binary search is a searching technique that is based upon the Divide-and-Conquer Rule.

In this searching technique, a sorted array is divided into two equal halves and then the same technique is applied onto the two halves searching for the element by comparing the high and the low.

binary
Time Complexity (Best) Ω(1)
Time Complexity (Avg) Θ(log n)
Time Complexity (Worst) O(log n)
Space Complexity O(1)

Working of binary search in JAVA

  1. For Binary Search to be performed on any array, the array must be already sorted in any format, that is, either ascending or descending.
  2. Find the middle index of the array/list.
  3. If the middle element is equal to the search element, Stop Searching.
  4. If the element that is to be searched is less then the middle element then consider the first half as a separate list.
  5. Else-If the element that is to be searched is larger then the middle element then consider the second half as a separate list.
  6. Repeat Step 2-3-4-5 Until desired result is found.

 

Algorithm of Binary Search in Java

  • while(left<=right)
          mid=left + (right – left)/2;
  • if(a[mid]<search_element)
          left=mid+1;
  • else if(a[mid]>search_element)
          right=mid-1;
  • If found return index+1
  • Else return -1
Binary Search in Java Example

Methods Discussed

We will be discussing two methods for the same

  • Recursive Approach
  • Iterative Approach

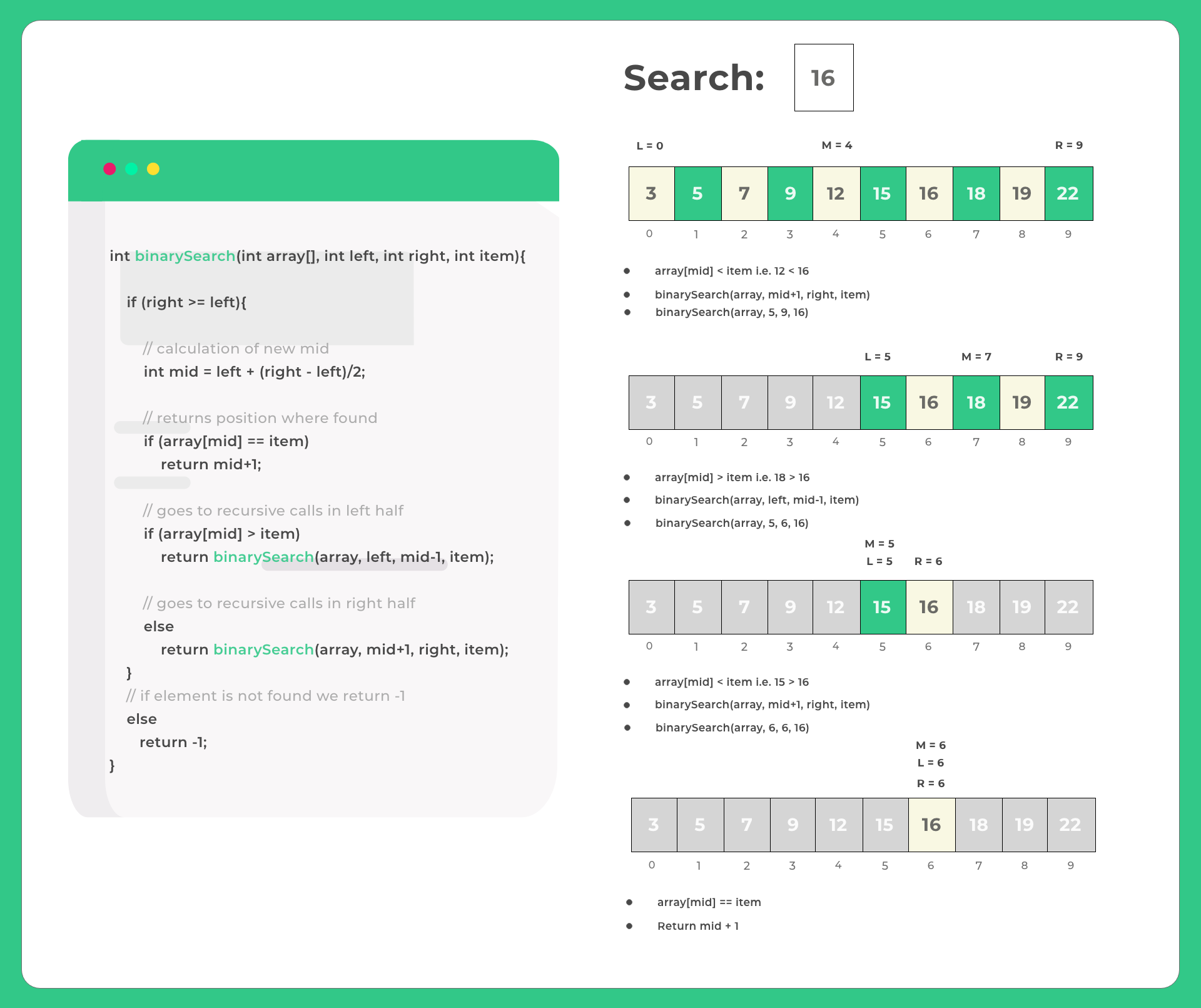
Binary Search in Java (Recursive Approach)

Run 
// Binary Search implimentation in Java (Recursive)
// Time Complexity : O(N)
// Space Complexity : O(1)
// Auxiliary Space Complexity : O(N) due to function call stack
public class Main{

    public static int binarySearch(int array[], int left, int right, int item){

        if (right >= left){

            // calculation of new mid
            int mid = left + (right - left)/2;

            // returns position where found
            if (array[mid] == item)
                return mid+1;

            // goes to recursive calls in left half
            if (array[mid] > item)
                return binarySearch(array, left, mid-1, item);

                // goes to recursive calls in right half
            else
                return binarySearch(array, mid+1, right, item);
        }
        // if element is not found we return -1
        else
            return -1;
    }
    public static void main(String args[]){

        int[ ] array = {10, 20, 30, 40, 50, 60, 70, 80};
        int item = 70;
        int size = array.length;

        int position = binarySearch(array, 0, size-1, item);

        if(position == -1)
            System.out.println("Element not found");
        else
            System.out.println("The value " + item + " found at position: " + position);

    }
}
// Time complexity O(Log N)

Output

The value 70 found at position: 7

Binary Search in Java (Iterative Approach)

Let us look at the iterative approach below –

Run 
// Binary Search implementation in Java (Recursive)
// Time Complexity : O(N)
// Space Complexity : O(1)
// Auxiliary Space Complexity : O(N) due to function call stack
public class Main{

    public static int binarySearch(int arr[], int left, int right, int item){

        while (left <= right) {
            int mid = left + (right - left) / 2;

            // if item is at mid
            if (arr[mid] == item)
                return mid;

            // If item greater, ignore left half, consider only right half
            if (arr[mid] < item)
                left = mid + 1;

                // If item is smaller, ignore right half, consider only left half
            else
                right = mid - 1;
        }

        // if we are able to reach here
        // means item wasn't present
        return -1;
    }
    public static void main(String args[]){

        int[ ] array = {10, 20, 30, 40, 50, 60, 70, 80};
        int item = 70;
        int size = array.length;

        int position = binarySearch(array, 0, size-1, item);

        if(position == -1)
            System.out.println("Element not found");
        else
            System.out.println("The value " + item + " found at position: " + position);

    }
}

Output

The value 70 found at position: 6

Time Complexity
For Binary Search

Best

O(1)

Average

O(log n)

Worst

O(log n)

Space Complexity

O(1)

Data Structures and Algorithm Learn Searching PrepInsta

Searching

Searching algorithms are easy to learn but are really important for college semester exams and companies offering package between 3 – 6 LPA would ask direct searching questions in online test/ interviews.