Binary Search in Java
Binary Search in Java Programming Language
Before moving on to Binary search in Java language….let you know that it is a fundamental algorithm in computer science used to efficiently find an element in a sorted array.
Unlike linear search, which checks each element one by one, binary search divides the array into halves and eliminates one half during each iteration, significantly reducing the number of comparisons.
This article will cover the concept, implementation, time complexity, variations, and practical applications of Binary Search in Java.

So, for clear understanding of concept of Binary Search we have share the algorithm for Binary Search for Java alongwith Java code. Here’s how:
How Binary Search Works ?
- Binary search operates by repeatedly dividing the search interval in half.
- If the target value is less than the middle element, the algorithm continues the search on the left half.
- If the target value is greater, it searches the right half.
- This process continues until the target value is found or the search interval is empty.
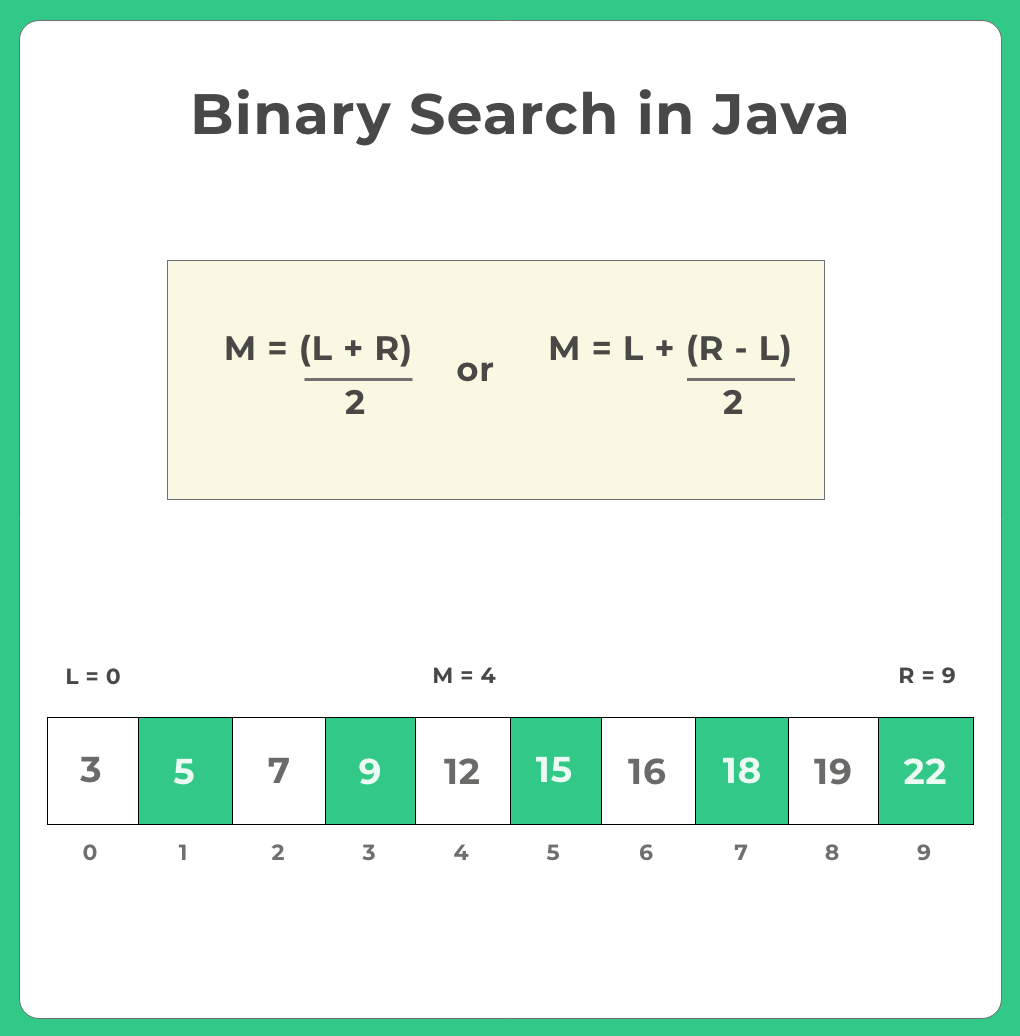
Binary Search Algorithm: Step by Step
- Initialization: Set low = 0 and high = array.length – 1.
- Calculation of Midpoint: mid = low + (high – low) / 2
- Comparison:
- If array[mid] == target, return mid.
- If array[mid] < target, update low = mid + 1.
- If array[mid] > target, update high = mid – 1.
- Termination: The algorithm terminates when low > high or when the target value is found.
Space and Time Complexity
| Time Complexity (Best) | Ω(1) |
| Time Complexity (Avg) | Θ(log n) |
| Time Complexity (Worst) | O(log n) |
| Space Complexity | O(1) |
Edge Cases and Considerations
- Handling overflow when calculating the midpoint using low + (high – low) / 2.
- Ensuring that the array is sorted before applying binary search.
- Dealing with duplicate elements in the array.
Learn DSA
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Methods Discussed
We will be discussing two methods for the same
- Recursive Approach
- Iterative Approach
1. Binary Search in Java (Recursive Approach)
Iterative approach uses a loop to repeatedly divide the search space in half.
It maintains
lowandhighpointers and adjusts them based on the comparison with the middle element.This approach is space efficient as it does not require additional stack space.
Advantages:
- More space efficient compared to recursion.
- Easier to debug and trace since it avoids stack overflow issues.
Disadvantages:
The logic can be slightly more complex compared to recursion due to explicit handling of the loop.
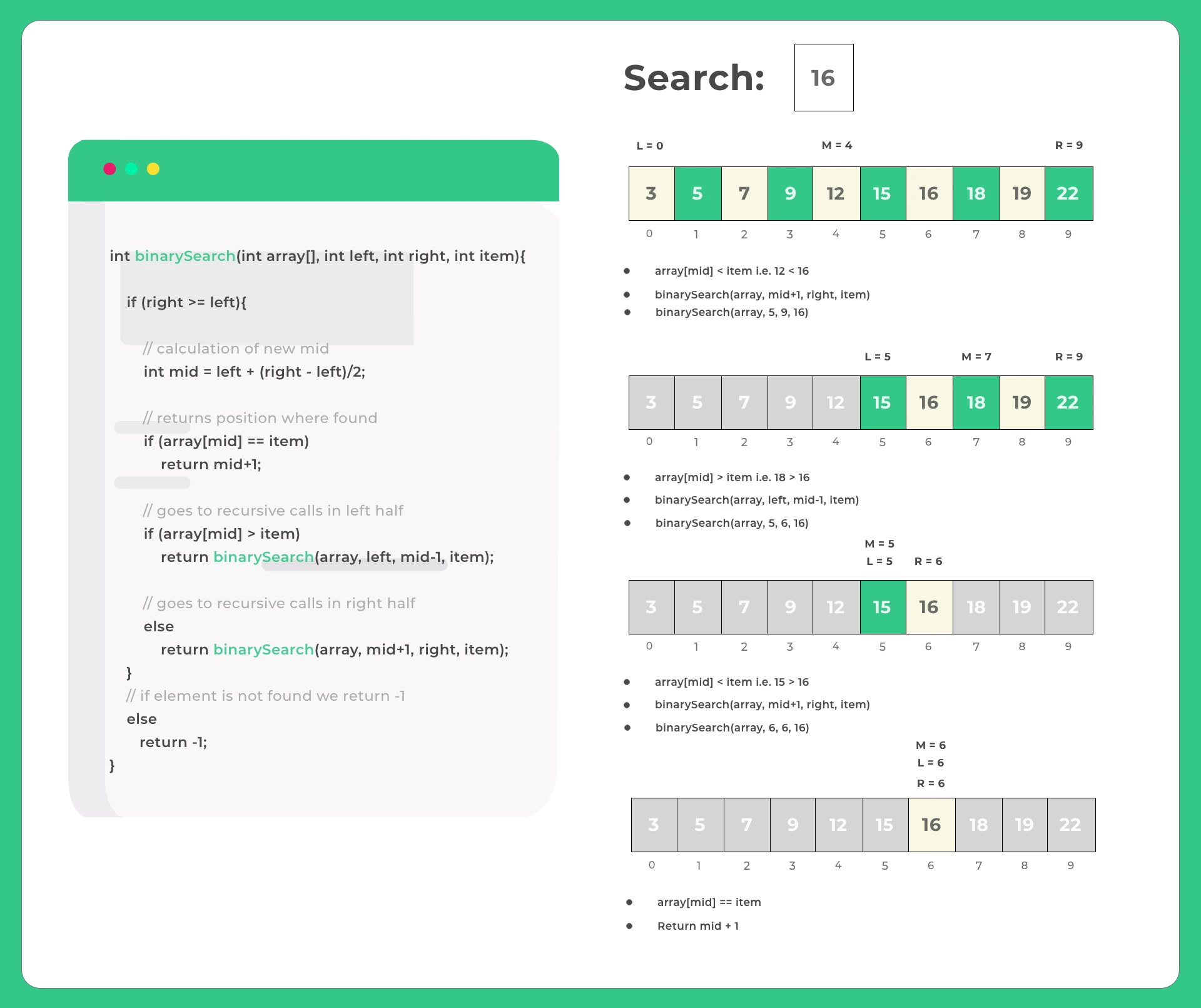
// Binary Search implimentation in Java (Recursive)
// Time Complexity : O(N)
// Space Complexity : O(1)
// Auxiliary Space Complexity : O(N) due to function call stack
public class Main{
public static int binarySearch(int array[], int left, int right, int item){
if (right >= left){
// calculation of new mid
int mid = left + (right - left)/2;
// returns position where found
if (array[mid] == item)
return mid+1;
// goes to recursive calls in left half
if (array[mid] > item)
return binarySearch(array, left, mid-1, item);
// goes to recursive calls in right half
else
return binarySearch(array, mid+1, right, item);
}
// if element is not found we return -1
else
return -1;
}
public static void main(String args[]){
int[ ] array = {10, 20, 30, 40, 50, 60, 70, 80};
int item = 70;
int size = array.length;
int position = binarySearch(array, 0, size-1, item);
if(position == -1)
System.out.println("Element not found");
else
System.out.println("The value " + item + " found at position: " + position);
}
}
// Time complexity O(Log N)
Output
The value 70 found at position: 7
Space Complexity = O(log n)
Time Complexity = O(log n)
Binary Search in Java (Iterative Approach)
Let us look at the iterative approach below:
The recursive approach calls the same function with adjusted
lowandhighpointers based on the comparison.It uses the call stack to keep track of the current state, resulting in a space complexity of O(log n).
Advantages:
- Simplified logic due to inherent stack structure.
- Easier to implement and understand in terms of algorithmic flow.
Disadvantages:
- Additional space overhead due to recursive stack frames.
- Risk of stack overflow for large arrays.
// Binary Search implementation in Java (Recursive)
// Time Complexity : O(N)
// Space Complexity : O(1)
// Auxiliary Space Complexity : O(N) due to function call stack
public class Main{
public static int binarySearch(int arr[], int left, int right, int item){
while (left <= right) {
int mid = left + (right - left) / 2;
// if item is at mid
if (arr[mid] == item)
return mid;
// If item greater, ignore left half, consider only right half
if (arr[mid] < item)
left = mid + 1;
// If item is smaller, ignore right half, consider only left half
else
right = mid - 1;
}
// if we are able to reach here
// means item wasn't present
return -1;
}
public static void main(String args[]){
int[ ] array = {10, 20, 30, 40, 50, 60, 70, 80};
int item = 70;
int size = array.length;
int position = binarySearch(array, 0, size-1, item);
if(position == -1)
System.out.println("Element not found");
else
System.out.println("The value " + item + " found at position: " + position);
}
}Output
The value 70 found at position: 6
Space Complexity = O(1)
Time Complexity = O(log n)
Conclusion:
- Binary search is an efficient algorithm for finding elements in a sorted array with a time complexity of O(log n).
- The iterative approach uses constant space, while the recursive approach uses additional space due to the call stack.
- Choosing between them depends on space constraints and implementation preference.
Learn DSA

FAQ's related to Binary Search in Java
Answer:
Time complexity of binary search in Java is O(log n) in both recursive and iterative methods.
Answer:
Because each recursive call adds a new frame to the call stack, resulting in a space complexity of O(log n).
Answer:
Iterative binary search repeatedly divides the search range in half using a loop until the target is found or the range is empty.
Answer:
Iterative binary search is generally preferred due to its constant space complexity O(1) compared to O(log n) for the recursive method.
Answer:
No, binary search requires the array to be sorted in ascending order for it to work correctly.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others





Login/Signup to comment