Insertion Sort in Java
Insertion Sort in Java Programming
In this article, we’ll explore Insertion Sort in Java, covering its algorithm, working process, Java implementation, and time-space complexity along with examples for better understanding.
Insertion Sort is a basic and easy to understand sorting algorithm. It works similarly to how we sort playing cards in our hand by picking one card at a time and placing it in the right position. Although it’s not very efficient for large amounts of data, it works well for small datasets or lists that are already nearly sorted.

What is Insertion Sort?
Insertion Sort is a comparison based sorting algorithm that builds the final sorted array one element at a time. It works by taking one element from the input array and inserting it into its correct position in the sorted part of the array.
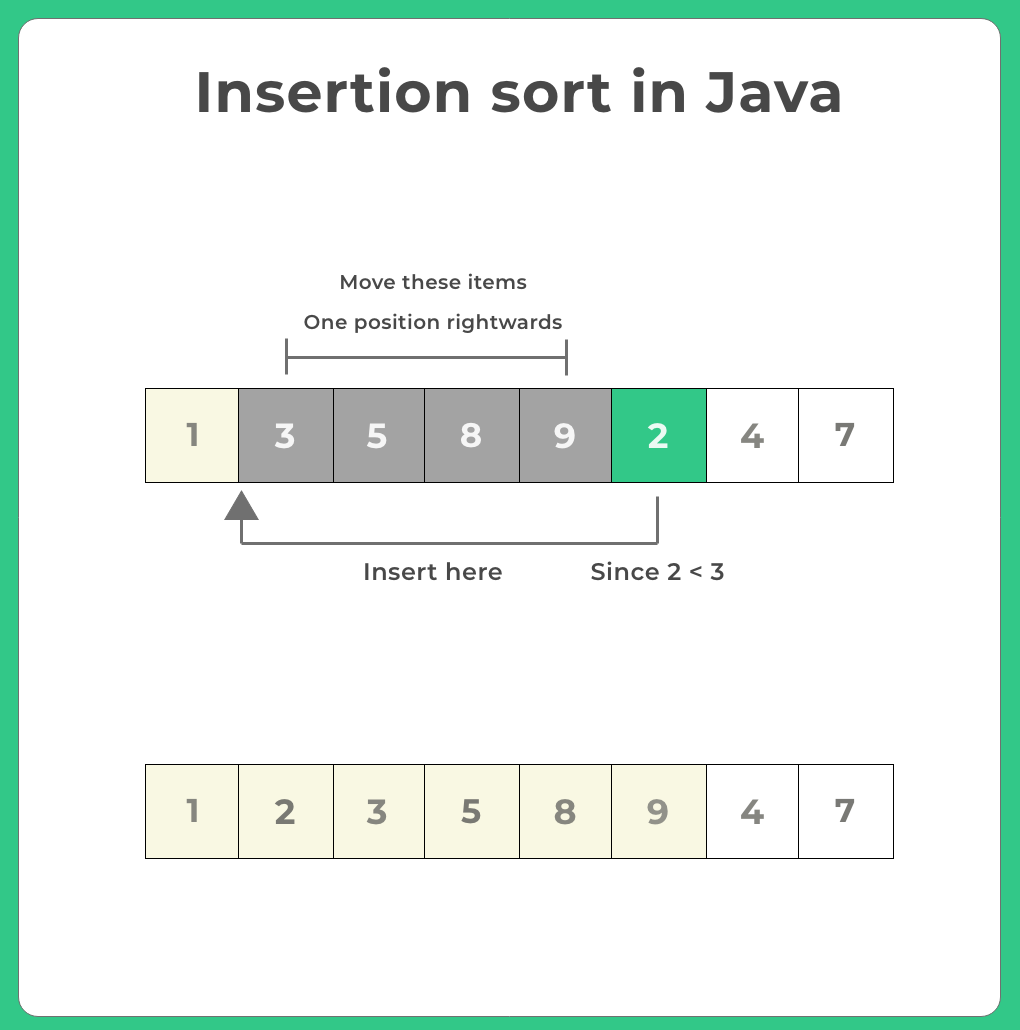
Step by Step Algorithm for Insertion Sort
Let’s go through the step by step explanation of how the Insertion Sort algorithm works:
- Start from the second element (index 1), as the single element at index 0 is considered sorted.
- Compare the current element with the elements before it.
- Shift all elements greater than the current element to one position ahead.
- Insert the current element into its correct position.
- Repeat steps 2–4 for all elements.
Algorithm Pseudocode
for i = 1 to n-1:
key = array[i]
j = i - 1
while j >= 0 and array[j] > key:
array[j + 1] = array[j]
j = j - 1
array[j + 1] = key
Learn DSA
Prime Course Trailer
Related Banners
Java Program for Insertion Sort
public class InsertionSortExample {
public static void insertionSort(int[] arr) {
int n = arr.length;
for (int i = 1; i < n; i++) { int key = arr[i]; int j = i - 1; // Shift elements of arr[0..i-1], that are greater than key while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
public static void printArray(int[] arr) {
for (int num : arr) {
System.out.print(num + " ");
}
System.out.println();
}
public static void main(String[] args) {
int[] arr = { 12, 11, 13, 5, 6 };
System.out.println("Original Array:");
printArray(arr);
insertionSort(arr);
System.out.println("Sorted Array:");
printArray(arr);
}
}
Input:
Original Array: 12 11 13 5 6
Output:
Sorted Array: 5 6 11 12 13
Time and Space Complexity Analysis for Insertion Sort
| Case | Comparisons | Time Complexity |
|---|---|---|
| Best Case | Already Sorted | O(n) |
| Average Case | Random Order | O(n²) |
| Worst Case | Reverse Order | O(n²) |
Stable Sorting Algorithm
Insertion sort is a stable sorting algorithm because it preserves the relative order of elements with equal keys.
Example:
Before Sorting: [3a, 2, 3b, 1]
After Sorting: [1, 2, 3a, 3b] (Order of 3a and 3b is preserved)
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription


Recursive Implementation of Insertion Sort in Java
Though insertion sort is usually implemented iteratively, it can also be implemented recursively.
public class RecursiveInsertionSort {
public static void insertionSortRecursive(int[] arr, int n) {
if (n <= 1) return; insertionSortRecursive(arr, n - 1); int last = arr[n - 1]; int j = n - 2; while (j >= 0 && arr[j] > last) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = last;
}
public static void main(String[] args) {
int[] arr = {9, 7, 5, 3, 1};
insertionSortRecursive(arr, arr.length);
for (int num : arr) {
System.out.print(num + " ");
}
}
}
Output:
1 3 5 7 9
Advantages and Disadvantages of Insertion Sort:
Advantages:
- Simple to implement and understand.
- Efficient for small or nearly sorted datasets.
- In place and stable.
Disadvantages:
- Not efficient on large datasets.
- Time complexity grows quadratically with input size.
To wrap it up….
Insertion Sort is a foundational sorting algorithm in computer science, valued for its simplicity and usefulness with small or nearly sorted data.
While it doesn’t scale well to large datasets due to its O(n²) time complexity, its in place and stable nature makes it a useful tool in specific scenarios and a common interview topic.
By understanding its algorithm, step by step implementation in Java, and space/time complexity, you gain a stronger grasp of how basic sorting mechanisms work, which is essential for advancing to more complex algorithms.

FAQ's related to Insertion Sort in Java
Answer:
When dealing with small datasets or nearly sorted data. It is also used as a subroutine in hybrid sorting algorithms.
Answer:
Yes, in practice. Although both have O(n²) complexity, insertion sort is more efficient than bubble sort in most real world scenarios.
Answer:
It doesn’t change the order of equal elements. When inserting an element, it only shifts greater elements to the right.
Answer:
Yes, insertion sort works for all integers including negative numbers.
Answer:
O(1), as it is an in place sorting algorithm and doesn’t require additional memory.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others




Login/Signup to comment