Programming
Aptitude
Syllabus
Interview Preparation
Interview Exp.
Off Campus
Merge Sort in Java
Merge Sort in Java Programming Language
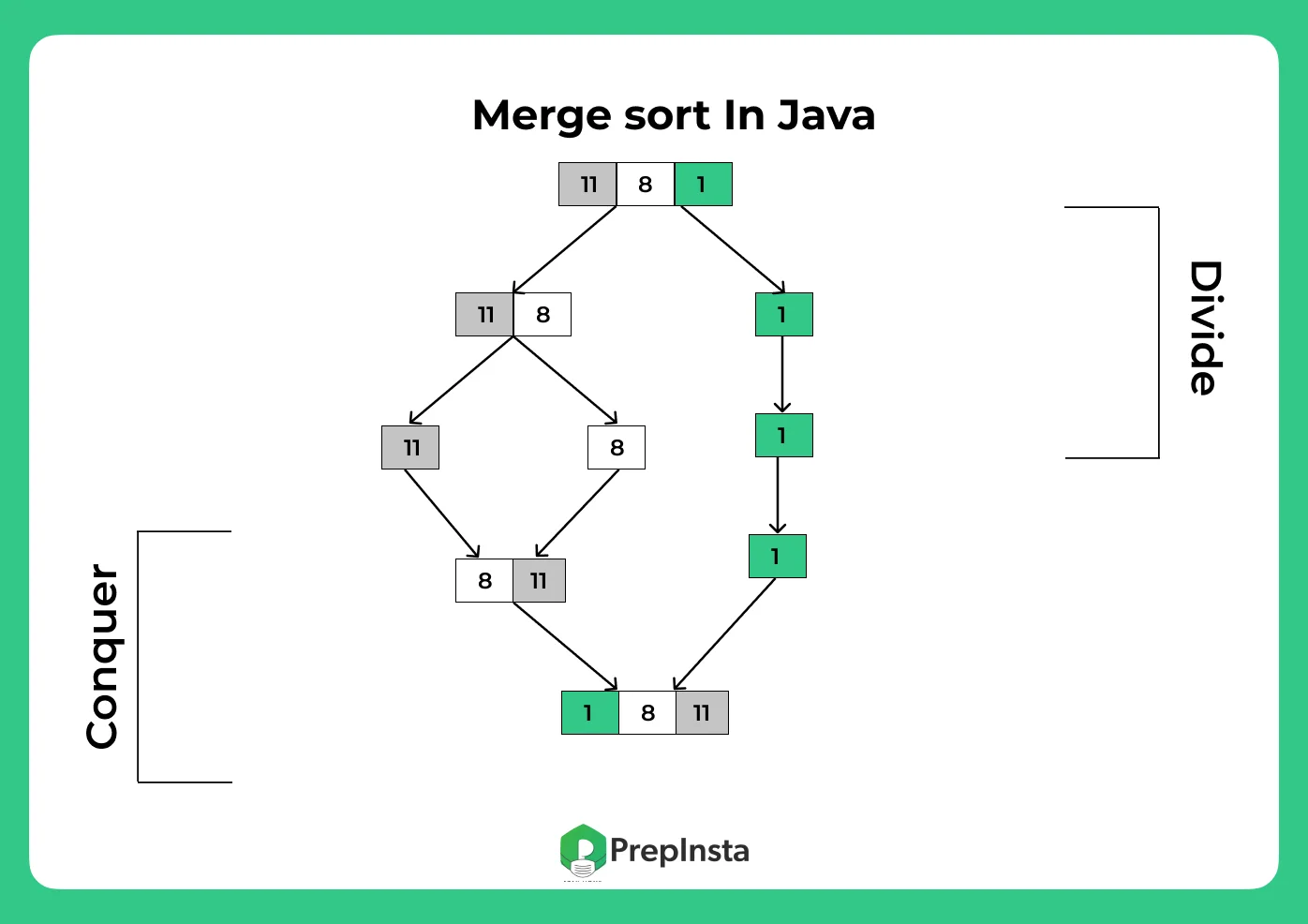
Merge Sort is a Divide & Conquer principle based algorithm, like its cousin Quick Sort. The main idea of merge sort is to divide large data-sets into smaller sets of data, and then solve them. Merge Sort is a recursive algorithm, it divides the given array into smaller half’s and then calls itself repeatedly to solve them.
| Time Complexity | Θ(n Log n) |
| Best Case | Ω(n Log n) |
| Worst Case | O(n Log n) |
| Space Complexity | O(n) |
Steps for Merge Sort in Java
Divide
- The original array is divided into sub-arrays.
- The sub-arrays are further divided into further sub-arrays until they contain a single element using recursion.
Conquering/ Merging
- Then the sub-lists are combined together in the desired (sorted) order.
- The time complexity of the merge sort is O(n log n) for best/ worst / average cases.
Implementation of Merge Sort in JAVA
Program for Merge Sort in Java
We will look at two different variations –
- Method 1: Works with two sub-arrays
- Method 2: Works with one sub-array
The space complexity is the same i.e. O(n) in both cases as even though there are two subarrays in method 1 they in total have n array items and method 2 also with one single array also has n array items.
Two SubArrays
//Java Program for Merge Sort
class Main {
// this function display the array
public static void display(int[] arr, int size)
{
for(int i = 0; i < size; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
// main function of the program
public static void main(String[] args)
{
int[] a = {12, 8, 4, 14, 36, 64, 15, 72, 67, 84};
int size = a.length;
display(a, size);
mergeSort(a, 0, size - 1);
display(a, size);
}
// this function apply merging and sorting in the array
static void mergeSort(int[] a, int left, int right)
{
int mid;
if(left < right)
{
// can also use mid = left + (right - left) / 2
// this can avoid data type overflow
mid = (left + right) / 2;
// recursive calls to sort first half and second half sub-arrays
mergeSort(a, left, mid);
mergeSort(a, mid + 1, right);
merge(a, left, mid, right);
}
}
// after sorting this function merge the array
static void merge(int[] arr, int left, int mid, int right)
{
int i, j, k;
int n1 = mid - left + 1;
int n2 = right - mid;
// create temp arrays to store left and right sub-arrays
int L[] = new int[n1];
int R[] = new int[n2];
// Copying data to temp arrays L[] and R[]
for (i = 0; i < n1; i++)
L[i] = arr[left + i];
for (j = 0; j < n2; j++)
R[j] = arr[mid + 1 + j];
// here we merge the temp arrays back into arr[l..r]
i = 0; // Starting index of L[i]
j = 0; // Starting index of R[i]
k = left; // Starting index of merged sub-array
while (i < n1 && j < n2)
{
// place the smaller item at arr[k] pos
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
}
else {
arr[k] = R[j];
j++;
}
k++;
}
// Copy the remaining elements of L[], if any
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
// Copy the remaining elements of R[], if any
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
}Output
12 8 4 14 36 64 15 72 67 84 4 8 12 14 15 36 64 67 72 84
One Subarray
//Java Program for Merge Sort
class Main {
// this function display the array
public static void display(int[] arr, int size)
{
for(int i = 0; i < size; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
// main function of the program
public static void main(String[] args)
{
int[] a = {12, 8, 4, 14, 36, 64, 15, 72, 67, 84};
int size = a.length;
display(a, size);
mergeSort(a, 0, size - 1);
display(a, size);
}
// this function apply merging and sorting in the array
static void mergeSort(int[] a, int left, int right)
{
int mid;
if(left < right)
{
// can also use mid = left + (right - left) / 2
// this can avoid data type overflow
mid = (left + right) / 2;
// recursive calls to sort first half and second half sub-arrays
mergeSort(a, left, mid);
mergeSort(a, mid + 1, right);
merge(a, left, mid, right);
}
}
// after sorting this function merge the array
static void merge(int[] a, int left, int mid, int right)
{
int i = left; // starting index of left sub-array
int j = mid + 1; // starting index of right sub-array
int index = left; // used to place items in temp[]
int[] temp = new int[10];
while(i <= mid && j <= right)
{
// place the smaller item at temp[index]
if(a[i] < a[j])
{
temp[index] = a[i];
i = i + 1;
}
else
{
temp[index] = a[j];
j = j + 1;
}
index++;
}
// i > mid would mean all items for left
// sub-array were successfully placed, and there
// must be unplaced right sub-array items
if(i > mid)
{
while(j <= right) {
temp[index] = a[j];
index++;
j++;
}
}
else {
while(i <= mid)
{
temp[index] = a[i];
index++;
i++;
}
}
int p = left;
while(p < index)
{
a[p] = temp[p];
p++;
}
}
}Output
12 8 4 14 36 64 15 72 67 84 4 8 12 14 15 36 64 67 72 84
Merge Sort Analysis
- Merge sort is quick algorithm and does sorting in only O(n log n) time
- However, it comes with a cost, which is extra space complexity which is too high in comparison to others which is o(n)
- While, one good thing is there that for all cases, the time complexity remains the same i.e. average, best, worst
Sorting
Sorting algorithms are easy to learn but are really important for college semester exams and companies offering package between 3 – 6 LPA would ask direct searching questions in online test/ interviews.
Login/Signup to comment