Find Zeros to be Flipped so that number of Consecutive 1s is maximized in Java
Maximum Consecutive Ones After Flipping Zeroes in Java
In coding interviews, Maximum Consecutive Ones After Flipping Zeroes in Java is a common problem related to binary arrays and consecutive sequences where you need to find which zeros to flip to maximize continuous 1s.
This problem focuses on finding which zeros in a binary array should be flipped to 1s to get the longest possible sequence of consecutive 1s. It’s a great example of how array manipulation and sliding window techniques can be used together to solve real world optimization problems.

Find Zeros to be Flipped so that number of Consecutive 1s is maximized
What is the Problem?
You are given a binary array (an array consisting only of 0’s and 1’s) and a number m, which represents the maximum number of zeros you are allowed to flip to 1.
Your task:
Find the indices of zeros that should be flipped so that the maximum number of consecutive 1’s can be obtained in the array.
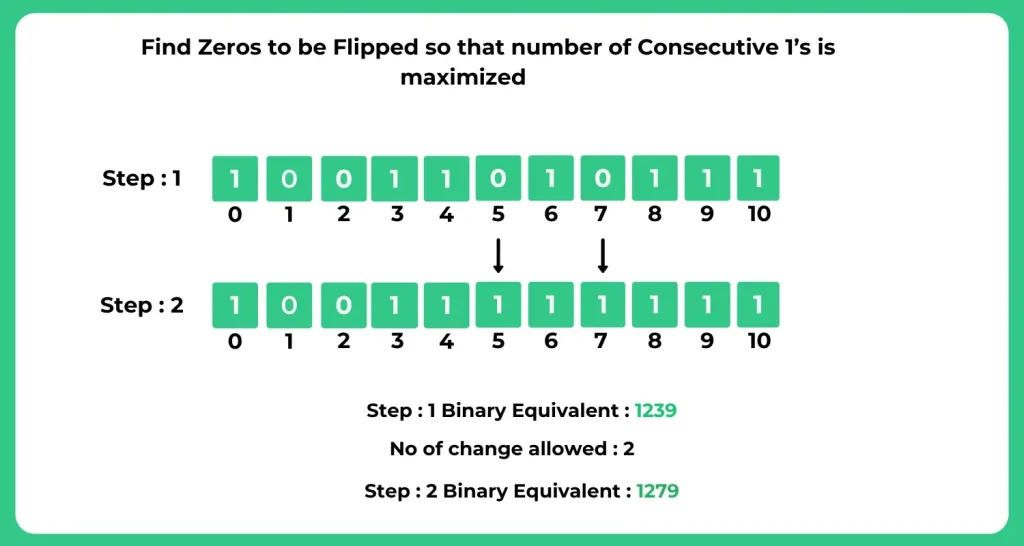
Example:
Input:
arr = {1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1}
m = 2Output: Indices of zeros to be flipped: [5, 7]
Explanation:
If we flip the zeros at positions 5 and 7, the array becomes:
{1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1}
Now, the maximum number of consecutive 1’s = 8.
Approach to Maximum Consecutive Ones After Flipping Zeroes
To find Zeros to be Flipped so that number of Consecutive 1s is maximized using Java, we can use 3 approaches mentioned below:
Hence, we must find the maximum window of the array that contains at most m zeros.
Learn DSA
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Approach for Maximum Consecutive Ones After Flipping Zeroes in Java
Approach 1: Brute Force Method
Problem: Check every possible subarray of the array, count the number of zeros, and track the maximum length of a subarray that contains at most m zeros.
This is a simple but inefficient approach suitable for understanding the basic logic.
Algorithm:
- Initialize maxLen = 0.
- Loop i from 0 to n-1:
Initialize zeroCount = 0.
Loop j from i to n-1:
If arr[j] == 0, increment zeroCount.
If zeroCount exceeds m, break.
Update maxLen if (j – i + 1) is greater.
- Return maxLen.
Code:
public class MaxConsecutiveOnesBruteForce {
public static int findMaxConsecutiveOnes(int[] arr, int m) {
int n = arr.length;
int maxLen = 0;
for (int i = 0; i < n; i++) {
int zeroCount = 0;
for (int j = i; j < n; j++) { if (arr[j] == 0) zeroCount++; if (zeroCount > m) break;
maxLen = Math.max(maxLen, j - i + 1);
}
}
return maxLen;
}
public static void main(String[] args) {
int[] arr = {1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1};
int m = 2;
System.out.println("Maximum consecutive 1's after flipping at most " + m + " zeros: "
+ findMaxConsecutiveOnes(arr, m));
}
}
Output:
Maximum consecutive 1's after flipping at most 2 zeros: 8
Space Complexity: O(1) - No extra data structures used.
Approach 2: Sliding Window (Optimized Approach)
Problem: Instead of checking every subarray, we use a window (or two pointer technique) to dynamically maintain a range of elements that contains at most m zeros.
Whenever the count of zeros exceeds m, we shrink the window from the left side until the number of zeros becomes valid again.
This approach is optimal and widely asked in interviews.
Algorithm:
- Initialize left = 0, right = 0, zeroCount = 0, and bestWindow = 0.
- Traverse the array using right pointer:
If arr[right] == 0, increment zeroCount.
If zeroCount > m, move left pointer forward until zeroCount <= m.
Update the maximum window size.
- To find which zeros to flip, track their indices inside the window.
Code:
import java.util.*;
public class MaxConsecutiveOnesSlidingWindow {
public static List findZerosToFlip(int[] arr, int m) {
int left = 0, right = 0;
int zeroCount = 0;
int bestLeft = 0, bestWindow = 0;
int n = arr.length;
while (right < n) {
if (arr[right] == 0)
zeroCount++;
// Shrink window from left if zero count exceeds m
while (zeroCount > m) {
if (arr[left] == 0)
zeroCount--;
left++;
}
// Update the best window
if (right - left + 1 > bestWindow) {
bestWindow = right - left + 1;
bestLeft = left;
}
right++;
}
// Collect zero indices in the best window
List result = new ArrayList<>();
for (int i = bestLeft; i < bestLeft + bestWindow; i++) {
if (arr[i] == 0)
result.add(i);
}
return result;
}
public static void main(String[] args) {
int[] arr = {1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1};
int m = 2;
List result = findZerosToFlip(arr, m);
System.out.println("Indices of zeros to be flipped: " + result);
}
}
Output:
Indices of zeros to be flipped: [5, 7]
Space Complexity: O(1) - Only a few variables are used.
Approach 3: Using Queue (Alternative Sliding Window)
Problem: Another variation of the sliding window uses a queue to store indices of zeros. When the count of zeros exceeds m, we remove the oldest zero index from the queue and move the left pointer accordingly.
This is slightly easier to understand for beginners.
Code:
import java.util.*;
public class MaxConsecutiveOnesQueue {
public static List findZerosToFlip(int[] arr, int m) {
Queue zeroIndices = new LinkedList<>();
int left = 0, right;
int bestLeft = 0, bestWindow = 0;
for (right = 0; right < arr.length; right++) {
if (arr[right] == 0)
zeroIndices.add(right);
if (zeroIndices.size() > m) {
left = zeroIndices.poll() + 1;
}
if (right - left + 1 > bestWindow) {
bestWindow = right - left + 1;
bestLeft = left;
}
}
List result = new ArrayList<>();
for (int i = bestLeft; i < bestLeft + bestWindow; i++) {
if (arr[i] == 0)
result.add(i);
}
return result;
}
public static void main(String[] args) {
int[] arr = {1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1};
int m = 2;
List zerosToFlip = findZerosToFlip(arr, m);
System.out.println("Indices of zeros to be flipped: " + zerosToFlip);
}
}
Output:
Indices of zeros to be flipped: [5, 7]
Space Complexity: O(m)(for storing zero indices)
Comparison of Methods for Maximum Consecutive Ones After Flipping Zeroes in Java
Among all the approaches, the Sliding Window and Queue Based Sliding Window methods are the most efficient for maximizing consecutive 1’s, both offering O(n) time complexity.
Brute Force approach is simple but slow due to its O(n²) complexity.
Hence, using a sliding window technique is the best balance between simplicity and performance.
| Approach | Logic Type | Time Complexity | Space Complexity | Efficiency |
|---|---|---|---|---|
| Brute Force | All subarrays | O(n2) | O(1) | Low |
| Sliding Window | Two-pointer method | O(n) | O(1) | High |
| Queue Based Sliding Window | Using queue | O(n) | O(m) | High |
Sliding window technique is the most efficient and elegant way to solve this problem.
Understanding this logic helps in solving related problems like:
- Longest subarray with at most k zeros
- Longest substring with k distinct characters
- Maximum number of ones after K flips
This problem is an excellent example of how sliding window algorithms simplify complex subarray problems in Java. Once you master this concept, you can solve many array and string related problems efficiently.
FAQ's on Finding Zeros to be Flipped so that number of Consecutive 1s is maximized
Answer:
It’s a binary array problem where we must identify which zeros to flip into ones to form the longest sequence of consecutive 1’s.
Answer:
Sliding Window Algorithm is the best choice. It runs in O(n) time and efficiently handles large inputs.
Answer:
You can use the two pointer sliding window approach to dynamically adjust the range while maintaining at most m zeros in the window.
Answer:
Time Complexity: O(n) and Space Complexity: O(1)
Answer:
Brute force checks all possible subarrays (O(n²)), while the sliding window approach scans the array once (O(n)) using dynamic range adjustment.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others







Login/Signup to comment