Largest Rectangular Area Under a Histogram Problem
Introduction to Largest Rectangular Area Under a Histogram Problem:
The Largest Rectangular Area Under a Histogram Problem in Python is a well-known algorithmic challenge that involves finding the maximum rectangular area that can be formed within a given histogram.
The goal is to determine the largest rectangle that can fit entirely under the histogram’s bars, using their heights as the heights of the rectangle.In this page, we will explore both the naïve and optimized approaches to tackle this challenging problem.
What is a Histogram?
A histogram is a graphical representation of the distribution of data. It consists of a series of vertical bars or bins, each representing a range of values, with the height of each bar indicating the frequency or count of data points falling within that range.
Why are Histograms Important?
Histograms provide valuable insights into the distribution of data, making them indispensable for data analysis, visualization, and decision-making in various fields such as statistics, finance, and engineering.
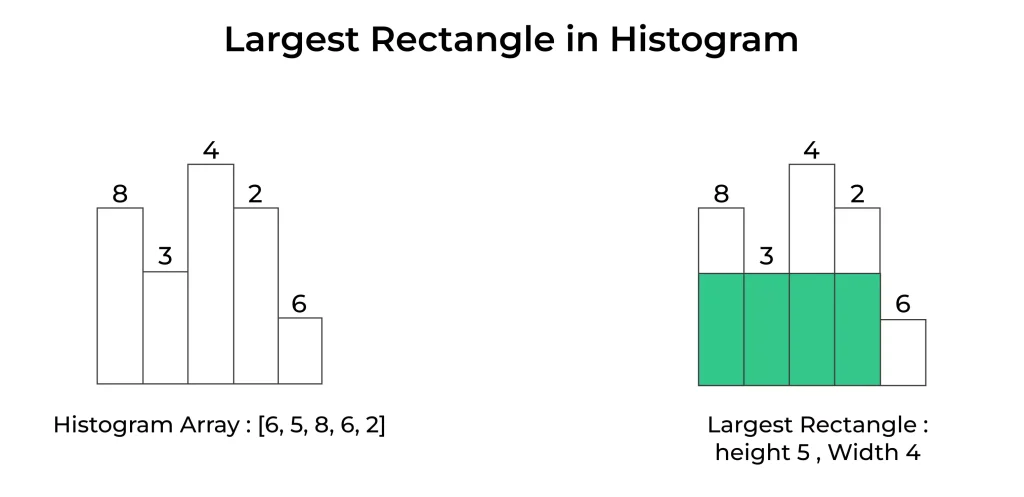
Largest Rectangular Area Under a Histogram Problem
Computing the Largest Rectangular Area
- Using Naïve Approach (Brute Force Solution)
- Using Optimized Approach (Using a Stack)
The Problem Statement
Given a histogram, our objective is to find the largest rectangular area that can be formed within it. This area can be visualized as a rectangle that spans several bars of the histogram, where the width of the rectangle corresponds to the number of bars, and the height is determined by the minimum bar height within that range.
Using Naïve Approach
Step 1: Consider All Possible Rectangles
The simplest way to approach this problem is to consider every possible rectangle within the histogram. To do this, you iterate through each bar in the histogram and, for each bar, check how far you can extend the rectangle to the left and right without violating the height constraints.
Step 2: Calculate the Area
For each rectangle, you calculate its area by multiplying its width (the difference between the right and left indices) by the minimum height among the bars within the rectangle.
Step 3: Keep Track of the Maximum Area
While going through all the rectangles, maintain a variable to store the maximum area encountered so far. This variable will eventually hold the answer to the problem.
Pseudocode
max_area = 0
for i in range(n):
for j in range(i, n):
min_height = min(heights[i:j+1])
area = min_height * (j - i + 1)
max_area = max(max_area, area)
Time Complexity Analysis
The time complexity of this approach is O(n^3), making it highly inefficient for larger histograms.
Optimized Approach
Algorithm Explanation
- Initialize an empty stack and a variable to store the maximum area.
- Iterate through each bar in the histogram.
- If the stack is empty or the current bar’s height is greater than the bar at the top of the stack, push the current bar’s index onto the stack.
- If the current bar’s height is less than or equal to the bar at the top of the stack, pop elements from the stack until we find a shorter bar or the stack becomes empty.
- For each popped element, calculate the area with the height of the popped bar and the width as the difference between the current index and the index at the top of the stack.
- Update the maximum area if the calculated area is greater.
- Repeat steps 3-6 until you traverse the entire histogram.
- Finally, pop the remaining elements from the stack and calculate the area using their heights and indices.
Pseudocode : Largest Rectangular Area Under a Histogram Problem
stack = []
max_area = 0
for i in range(n):
while stack and heights[i] <= heights[stack[-1]]:
top = stack.pop()
width = i if not stack else i - stack[-1] - 1
max_area = max(max_area, heights[top] * width)
stack.append(i)
while stack:
top = stack.pop()
width = n if not stack else n - stack[-1] - 1
max_area = max(max_area, heights[top] * width)
Time Complexity Analysis
The optimized approach has a time complexity of O(n), making it significantly more efficient than the naïve approach.
Example Naïve Approach (Brute Force Solution) :
def largestRectangleAreaNaive(heights):
max_area = 0
for i in range(len(heights)):
left = i
right = i
# Expand to the left
while left > 0 and heights[left - 1] >= heights[i]:
left -= 1
# Expand to the right
while right < len(heights) - 1 and heights[right + 1] >= heights[i]:
right += 1
# Calculate the area for the current bar
current_area = heights[i] * (right - left + 1)
# Update the maximum area if necessary
max_area = max(max_area, current_area)
return max_area
# Example usage:
histogram = [2, 1, 5, 6, 2, 3]
result = largestRectangleAreaNaive(histogram)
print("Largest rectangular area (Naïve Approach):", result)
Example Optimized Approach (Stack-Based) :
def largestRectangleAreaOptimized(heights):
stack = []
max_area = 0
for i in range(len(heights)):
while stack and heights[i] < heights[stack[-1]]:
height = heights[stack.pop()]
width = i if not stack else i - stack[-1] - 1
max_area = max(max_area, height * width)
stack.append(i)
while stack:
height = heights[stack.pop()]
width = len(heights) if not stack else len(heights) - stack[-1] - 1
max_area = max(max_area, height * width)
return max_area
# Example usage:
histogram = [2, 1, 5, 6, 2, 3]
result = largestRectangleAreaOptimized(histogram)
print("Largest rectangular area (Optimized Approach):", result) Conclusion
In conclusion, the problem of finding the largest rectangular area under a histogram is a fascinating challenge in the world of computer science. While a naïve approach exists, it is highly inefficient for larger datasets. The optimized approach, which employs a stack, offers a more efficient solution with a linear time complexity. Understanding and mastering such algorithms is crucial for tackling complex computational problems.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Question 1.
How is the largest rectangular area under a histogram relevant in image processing?
In image processing, this problem can be used to identify regions of interest within an image. By finding the largest rectangular area with specific characteristics, we can detect objects or patterns.
Question 2.
Are there any other applications for the optimized approach using a stack?
Yes, this approach is also used in various fields such as building skyline analysis, where it helps determine the skyline of a set of buildings given their heights.
Question 3.
Can the optimized approach handle histograms with negative heights?
No, the optimized approach assumes non-negative heights for the bars in the histogram. Negative heights would require additional handling.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Login/Signup to comment