Largest Rectangle with all 1s in Python
Introduction to Largest Rectangle with all 1s in Python:
The “Largest Rectangle with all 1s in Python” is a problem that involves finding the largest rectangle containing only 1s in a binary matrix. This algorithmic challenge is commonly encountered in computer science and is used in various applications, including image processing and data analysis.
This page we will discuss about how to compute the maximum size of a rectangle in a binary sub-matrix filled with ones, a problem that holds significance in various domains such as computer vision, image processing, and algorithm design.

What Is the Largest Rectangle with all 1's?
Imagine a binary matrix filled with zeros and ones. The objective is to determine the largest rectangular region within this matrix, where all the enclosed elements are ones. This rectangle can be oriented both horizontally and vertically.
The Importance of Solving this Problem
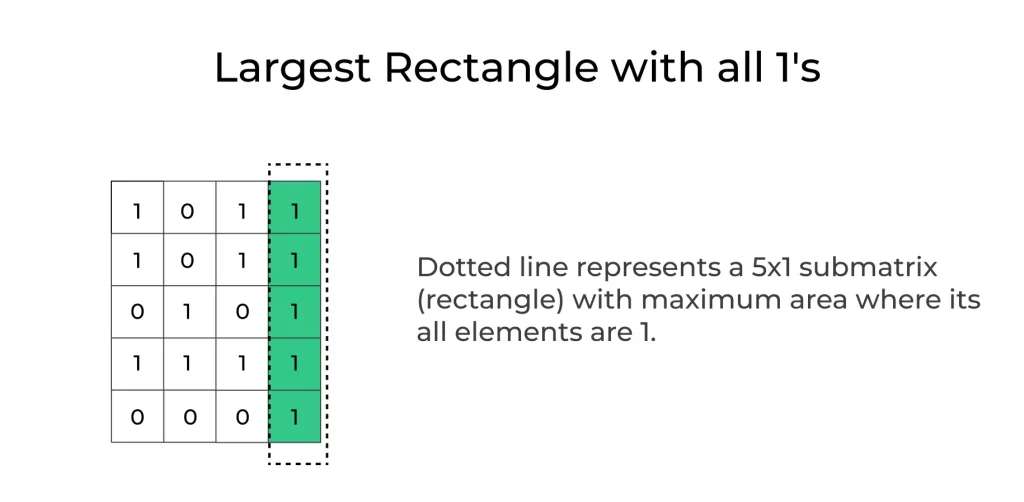
Algorithms for Finding the Largest Rectangle
def maximalRectangle(matrix): if not matrix: return 0 def maximalRectangleInHistogram(heights): stack = [] max_area = 0 for i, h in enumerate(heights): while stack and h < heights[stack[-1]]: height = heights[stack.pop()] width = i if not stack else i - stack[-1] - 1 max_area = max(max_area, height * width) stack.append(i) while stack: height = heights[stack.pop()] width = len(heights) if not stack else len(heights) - stack[-1] - 1 max_area = max(max_area, height * width) return max_area max_area = 0 for i in range(len(matrix)): if i == 0: heights = [int(x) for x in matrix[i]] else: for j in range(len(matrix[i])): if matrix[i][j] == '1': heights[j] += 1 else: heights[j] = 0 max_area = max(max_area, maximalRectangleInHistogram(heights)) return max_area # Example usage: matrix = [ ["1", "0", "1", "0", "0"], ["1", "0", "1", "1", "1"], ["1", "1", "1", "1", "1"], ["1", "0", "0", "1", "0"] ] result = maximalRectangle(matrix) print(result)
Output:
6
Explanation:
- Converts each row into a histogram of heights based on consecutive 1s.
- Uses a stack to find the largest rectangle in the histogram.
- For each row, updates histogram heights if ‘1’; resets to 0 if ‘0’.
- Calculates max area after processing each row.
- Returns the overall maximum rectangle area.
Time and Space Complexity:
| Complexity Type | Value |
| Time Complexity | O(rows × cols) |
| Space Complexity | O(cols) |
# Implementing the largest rectangle with all 1s using a Stack-Based Approach
def largestRectangle(matrix):
if not matrix:
return 0
def maxRectangleArea(heights):
stack = []
max_area = 0
index = 0
while index < len(heights): if not stack or heights[index] >= heights[stack[-1]]:
stack.append(index)
index += 1
else:
top = stack.pop()
width = index if not stack else index - stack[-1] - 1
max_area = max(max_area, heights[top] * width)
while stack:
top = stack.pop()
width = index if not stack else index - stack[-1] - 1
max_area = max(max_area, heights[top] * width)
return max_area
max_area = 0
for row in range(len(matrix)):
if row == 0:
heights = list(map(int, matrix[row]))
else:
for col in range(len(matrix[row])):
if matrix[row][col] == '1':
heights[col] += 1
else:
heights[col] = 0
max_area = max(max_area, maxRectangleArea(heights))
return max_area
# Example usage:
matrix = [
["1", "0", "1", "0", "0"],
["1", "0", "1", "1", "1"],
["1", "1", "1", "1", "1"],
["1", "0", "0", "1", "0"]
]
result = largestRectangle(matrix)
print(result)
Output:
6
Explanation:
- Converts each matrix row into histogram heights.
- Uses a stack to compute the largest rectangle in the histogram.
- If current height is greater, index is pushed to stack; else, pop and calculate area.
- Remaining stack elements are processed at the end.
- Tracks and updates the maximum area across all rows.
Time and Space Complexity:
| Complexity Type | Value |
| Time Complexity | O(rows × cols) |
| Space Complexity | O(cols) |
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
The Algorithm to Find the Largest Rectangle with all 1s in Python
The algorithm’s core idea is to maintain a histogram for each row of the binary matrix and apply the largest rectangle in a histogram algorithm to find the maximum rectangle in each row.
Create an auxiliary matrix
- We start by creating an auxiliary matrix of the same size as the input binary matrix. This auxiliary matrix will help us keep track of the cumulative number of 1s in each row.
Initialize the first row
- The first row of the auxiliary matrix is initialized to be the same as the first row of the binary matrix.
Populate the auxiliary matrix
- For the remaining rows (i.e., from the second row onwards), we populate the auxiliary matrix by summing up the corresponding elements in the binary matrix with the element above it. This process ensures that each cell in the auxiliary matrix represents the cumulative number of 1s in the original binary matrix up to that point.
Find the maximum rectangle
- With the auxiliary matrix prepared, we apply the largest rectangle in a histogram algorithm for each row. This algorithm efficiently identifies the maximum rectangle within a histogram, which is essentially a row in the auxiliary matrix.
Update the maximum area
- During this process, we keep track of the maximum area encountered so far. By the end of this step, we have the maximum size rectangle in the binary sub-matrix with all 1s.
Implementing the Algorithm to Find Largest Rectangle with all 1s
# Python program to find maximum
# size rectangle binary sub-matrix
# with all 1s
def maxHist(row):
stack = list()
max_area = 0
index = 0
while index < len(row):
if (not stack) or (row[stack[-1]] <= row[index]):
stack.append(index)
index += 1
else:
top_of_stack = stack.pop()
area = (row[top_of_stack] *
((index - stack[-1] - 1)
if stack else index))
max_area = max(max_area, area)
while stack:
top_of_stack = stack.pop()
area = (row[top_of_stack] *
((index - stack[-1] - 1)
if stack else index))
max_area = max(max_area, area)
return max_area
def maxRectangle(matrix):
if not matrix:
return 0
# Initialize the first row of
# the auxiliary matrix
result = maxHist(matrix[0])
# Iterate over the remaining rows
for i in range(1, len(matrix)):
for j in range(len(matrix[i])):
# Update the auxiliary matrix
if matrix[i][j]:
matrix[i][j] += matrix[i - 1][j]
# Calculate the maximum area
result = max(result, maxHist(matrix[i]))
return result
# Example usage
matrix = [
[0, 1, 1, 0],
[1, 1, 1, 1],
[1, 1, 1, 0],
]
print("Maximum size rectangle in binary sub-matrix with all 1s:", maxRectangle(matrix))
Output:
Maximum size rectangle in binary sub-matrix with all 1s: 6
Explanation:
- Treats each row as a histogram of vertical 1s.
- Uses the maxHist() function to compute the largest rectangle in a histogram.
- For each row, updates the histogram by adding heights from the row above.
- Computes the max area of 1s rectangle row by row.
- Returns the largest area found across all rows.
Time and Space Complexity:
| Complexity Type | Value |
| Time Complexity | O(rows × cols) |
| Space Complexity | O(cols) |
Practical Applications : Largest Rectangle with all 1s in Python
- Geographic Information Systems (GIS) : In GIS, where spatial data is represented as grids, identifying the largest rectangle with all ones is valuable for delineating geographic features and optimizing data storage.
- Binary Image Compression : In the field of binary image compression, this problem is instrumental in reducing the size of binary images, leading to faster transmission and storage savings.
To sum up:
The quest to find the largest rectangle with all ones in a binary matrix is a fascinating journey through the world of algorithms and their real-world applications. Whether in data compression, image processing, or geographic information systems, the ability to efficiently solve this problem unlocks new possibilities for optimizing and analyzing data.
FAQs
The idea is to treat each row as a histogram and apply the “Largest Rectangle in Histogram” approach. This is done row-by-row using dynamic programming for height accumulation.
Each row builds on the one above it by accumulating consecutive 1s, forming vertical bars. These bars are then used to calculate maximum rectangular area just like in a histogram.
The time complexity is O(rows × cols) since each row is processed with a histogram algorithm in linear time. Space complexity is O(cols) due to the stack used in histogram processing.
Yes, the approach works for any rectangular matrix of 0s and 1s. However, it doesn’t support jagged (irregular length) rows without additional preprocessing.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others



