Weighted and Directed Graphs
Introduction to weighted and Directed Graphs
Weighted and Directed Graph theory is a vital concept in computer science and mathematics, offering a powerful way to represent and analyze relationships between various entities.
Among the different types of graphs, weighted and directed graphs hold immense importance due to their ability to model intricate relationships with additional characteristics.
Weighted and Directed Graphs
Graphs consist of nodes (vertices) and edges that establish connections between these nodes.
- When discussing weighted graphs, the edges carry a value or weight that signifies the cost, distance, or any other parameter associated with the connection between nodes. In contrast, directed graphs feature edges with a specific direction, implying a one-way relationship between nodes.
- Widely Used: Weighted and directed graphs are used in fields like transportation, social media, and logistics.
- Real-World Modeling: They help model complex relationships, such as city maps with traffic weights or user interactions online.
- Optimization Tasks: Commonly applied in algorithms for shortest paths, route planning, and resource management.
Using heapq Module (Binary Heap):
Python provides a heapq module that allows you to implement a binary heap-based priority queue.
import heapq class PriorityQueueBinaryHeap: def __init__(self): self.elements = [] def enqueue(self, priority, value): heapq.heappush(self.elements, (priority, value)) def dequeue(self): if not self.is_empty(): return heapq.heappop(self.elements) def is_empty(self): return len(self.elements) == 0
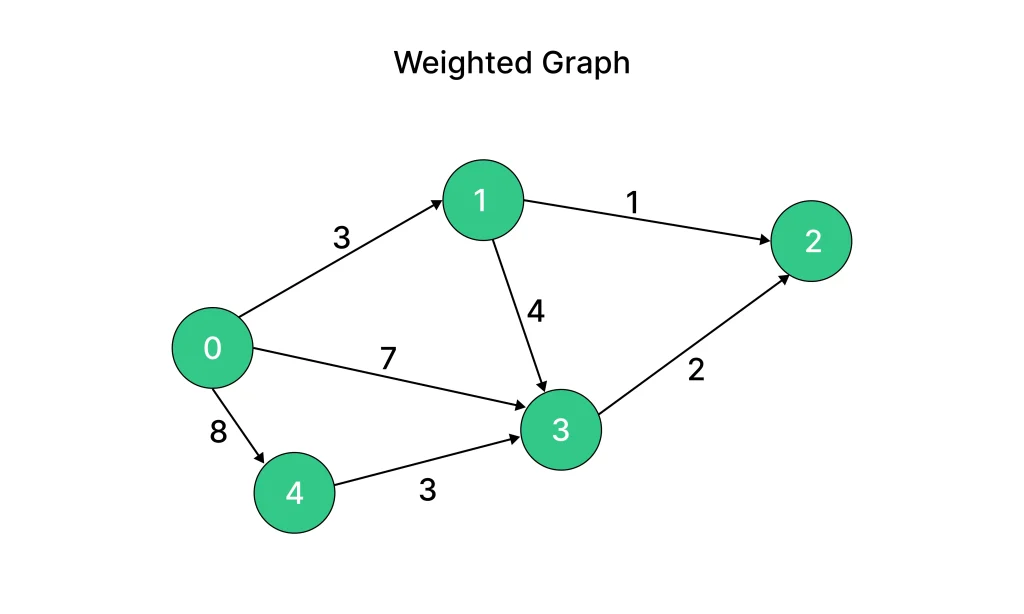
Example: Weighted Graph using Dictionary
Here’s a simple example of a Weighted Graph in Python using an adjacency list with weights, implemented using a dictionary. This code includes a sample graph, how to add edges, and how to display it.
class WeightedGraph:
def __init__(self):
self.graph = {}
def add_edge(self, u, v, weight):
# Add edge from u to v with weight
if u not in self.graph:
self.graph[u] = []
self.graph[u].append((v, weight))
# If undirected graph, add reverse edge
if v not in self.graph:
self.graph[v] = []
self.graph[v].append((u, weight))
def display(self):
for node in self.graph:
print(f"{node} --> {self.graph[node]}")
# Create a graph
g = WeightedGraph()
# Add edges (u, v, weight)
g.add_edge('A', 'B', 4)
g.add_edge('A', 'C', 2)
g.add_edge('B', 'C', 5)
g.add_edge('B', 'D', 10)
g.add_edge('C', 'D', 3)
# Display the graph
g.display()
Output:
A --> [('B', 4), ('C', 2)]
B --> [('A', 4), ('C', 5), ('D', 10)]
C --> [('A', 2), ('B', 5), ('D', 3)]
D --> [('B', 10), ('C', 3)]
Explanation:
- The graph is stored as a dictionary where each key is a node and the value is a list of tuples (neighbor, weight).
- This graph is undirected, so each edge is added in both directions.
- You can easily modify this to make it directed by removing the second part in add_edge.
Time and Space Complexity:
- Time Complexity: Adding an edge takes O(1) time since we’re using a dictionary and appending to a list.
- Space Complexity: The space used is O(V + E) where V is the number of vertices and E is the number of edges stored in the adjacency list.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Working with Directed Graphs in Python
Directed Graph Representation:
In Python, implementing directed graphs involves defining edges with a specified direction, enabling the modeling of one-way relationships between nodes.
Operations on Directed Graphs:
Manipulating directed graphs encompasses various operations like adding or removing nodes, modifying edges, and performing traversal or path-finding algorithms.
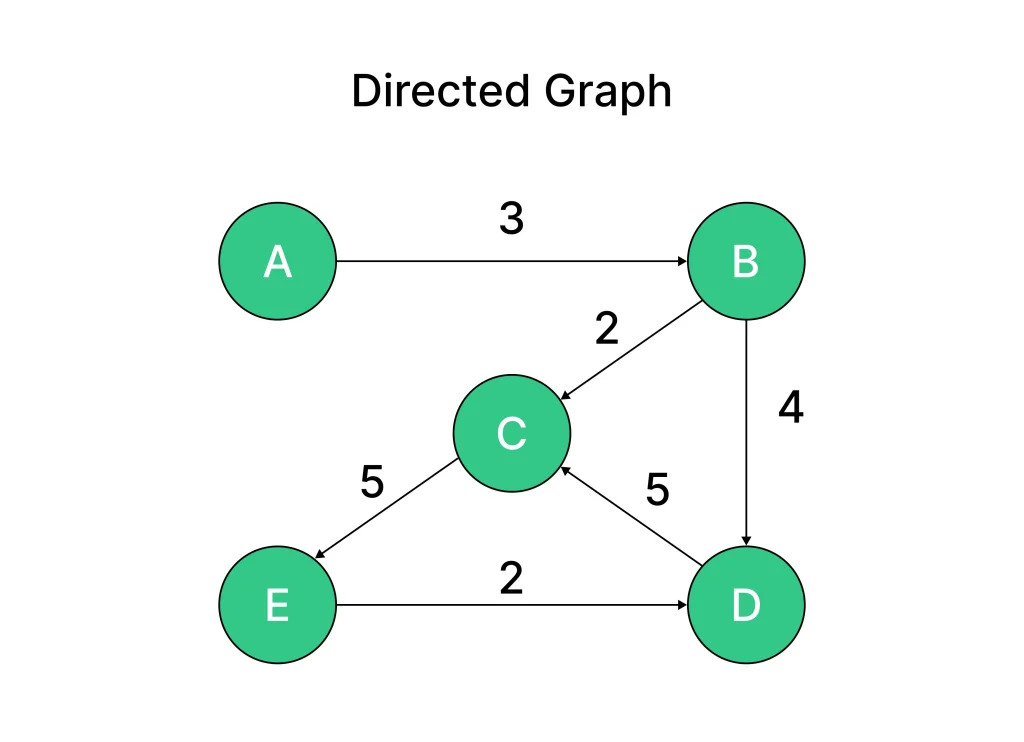
Example: Directed Graph
- Use a dictionary where each key is a node, and its value is a list of neighboring nodes it points to.
- Add directed edges using a helper method.
class DirectedGraph:
def __init__(self):
self.graph = {} # Adjacency list
def add_edge(self, u, v):
# Add edge from u to v (directed)
if u in self.graph:
self.graph[u].append(v)
else:
self.graph[u] = [v]
# Ensure v exists in graph
if v not in self.graph:
self.graph[v] = []
def display(self):
for node in self.graph:
print(f"{node} -> {self.graph[node]}")
# Example usage
g = DirectedGraph()
g.add_edge("A", "B")
g.add_edge("A", "C")
g.add_edge("B", "D")
g.add_edge("C", "D")
g.display()
Output:
A -> ['B', 'C'] B -> ['D'] C -> ['D'] D -> []
Explanation:
- Uses a dictionary to store nodes and their directed edges.
- add_edge(u, v) adds a one-way edge from u to v.
- display() prints each node and its outgoing links.
- Direction matters: u → v ≠ v → u.
Time and Space Complexity:
- Time Complexity:
- add_edge: O(1) per edge addition.
- display: O(V + E) where V = vertices, E = edges.
- Space Complexity:
- O(V + E) to store all vertices and directed edges.
To wrap it ip:
In conclusion, understanding weighted and directed graphs in Python provides a powerful toolset for modeling and solving real-world problems involving complex relationships. The ability to represent relationships with direction and magnitude enhances the applicability of graph structures in various domains.
FAQs
A Weighted and Directed Graph assigns a direction and weight (cost) to each edge between nodes. It’s commonly represented using adjacency lists or dictionaries in Python.
You can use a dictionary of dictionaries or adjacency list, where each key maps to its neighbors with edge weights. Libraries like networkx also simplify graph creation and manipulation.
networkx is the most popular library for handling complex graphs, including weighted and directed ones. igraph and graph-tool are also used for large-scale and efficient graph computations.
Dijkstra’s algorithm (for shortest paths) and Bellman-Ford (handles negative weights) are widely used. These are implemented manually or using built-in functions in networkx.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others




Login/Signup to comment