Time Complexity of recursive loops
Introduction to Time Complexity of Recursive Loops
Time complexity of Recursive Loops measures the time taken by an algorithm to solve a problem concerning the input size.
Time complexity is a measure of the computational resources an algorithm uses concerning the size of the input data. Recursive loops, a fundamental aspect of programming, play a significant role in understanding time complexity.
Definition of Recursive Loops:
Recursive loops involve a function that calls itself directly or indirectly in a self-referential manner.
- This programming technique breaks down a problem into smaller, more manageable subproblems until reaching a base case, providing elegant solutions to various complex problems.
- Recursive loops provide a clear and concise method for solving problems.
- They are especially useful for problems with a recursive mathematical definition (e.g., factorials, Fibonacci sequences).
- Recursion enhances code simplicity.
- It improves overall readability of the code.
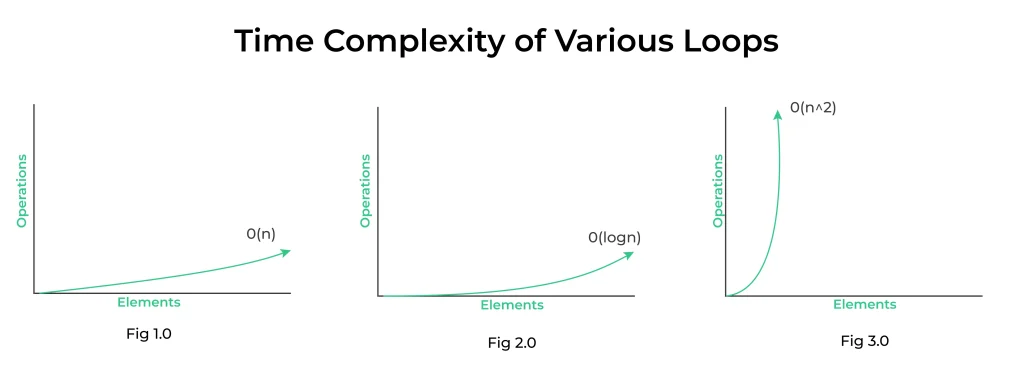
- Fig 1.0: Time complexity of a simple loop when the loop variable is incremented or decremented by a constant amount.
- Fig 2.0: Time complexity of a loop when the loop variable is divided or multiplied by a constant amount.
- Fig 3.0: Time complexity of a nested loop.
Prime Course Trailer
Related Banners
Methods to Calculate Time Complexity of recursive loops:
1. Counting Operations:
- Analyze the code and count the number of basic operations performed.
- Ignore constant factors and focus on the dominant term concerning input size.
2. Big O Notation:
- Express the upper bound of an algorithm’s growth rate.
- Example: O(n), O(n^2), O(log n).
3. Recurrence Relations:
- For recursive algorithms, formulate recurrence relations to express time complexity.
- Solve the recurrence relation to obtain a closed-form expression.
4. Master Theorem:
- Specifically used for divide-and-conquer algorithms with recursive relations.
- Provides a solution for a broad class of recurrence relations.
5. Amortized Analysis:
- Evaluate the average time taken per operation over a sequence of operations.
- Useful for data structures with varying operation costs.
6. Asymptotic Analysis:
- Focus on the behavior of an algorithm as the input size approaches infinity.
- Ignores constant factors and lower-order terms.
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Examples of Recursive Loops and Their Time Complexity:
def factorial(n):
if n == 0 or n == 1:
return 1
else:
return n * factorial(n - 1)
# Example usage
num = 5
result = factorial(num)
print(f"Factorial of {num} is: {result}")
Output:
Factorial of 5 is: 120
def fibonacci(n):
if n <= 0:
return 0
elif n == 1:
return 1
else:
return fibonacci(n - 1) + fibonacci(n - 2)
# Example usage
num = 6
result = fibonacci(num)
print(f"Fibonacci number at position {num} is: {result}")
Output:
Fibonacci number at position 6 is: 8
def merge_sort(arr):
if len(arr) <= 1:
return arr
# Divide the array into two halves
mid = len(arr) // 2
left_half = merge_sort(arr[:mid])
right_half = merge_sort(arr[mid:])
# Merge the sorted halves
return merge(left_half, right_half)
def merge(left, right):
result = []
i = j = 0
# Compare elements and merge
while i < len(left) and j < len(right):
if left[i] < right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
# Append remaining elements
result.extend(left[i:])
result.extend(right[j:])
return result
# Example usage
arr = [6, 3, 9, 1, 5]
sorted_arr = merge_sort(arr)
print(f"Sorted array: {sorted_arr}")
Output:
Sorted array: [1, 3, 5, 6, 9]
def binary_search(arr, target, low, high):
if low > high:
return -1 # Element not found
mid = (low + high) // 2
if arr[mid] == target:
return mid
elif target < arr[mid]:
return binary_search(arr, target, low, mid - 1)
else:
return binary_search(arr, target, mid + 1, high)
# Example usage
arr = [1, 3, 5, 7, 9, 11, 13]
target = 9
result = binary_search(arr, target, 0, len(arr) - 1)
if result != -1:
print(f"Element found at index: {result}")
else:
print("Element not found.")
Output:
Element found at index: 4
Time Complexity Analysis:
Basics of Time Complexity
- Time complexity measures the amount of time an algorithm takes to execute concerning the size of its input. It helps analyze the efficiency of an algorithm in solving a problem.
Factors Affecting Time Complexity
- Several factors impact Time Complexity of recursive loops, including the number of iterations, operations performed in each iteration, and recursive calls made within the algorithm.
Analyzing Time Complexity of recursive loops
- Recursive loops can have varying time complexities based on factors such as the number of recursive calls and the nature of operations within each call. Understanding this complexity is essential for optimizing code performance.
| Loop Type | Time Complexity (Big O Notation) | Description |
|---|---|---|
| For Loop: | O(n) | Iterates a fixed number of times (linear complexity). |
| While Loop: | O(n) | Iterates until a certain condition is met (linear complexity). |
| Nested Loop: | O(n^k) | k nested loops, each iterating n times (exponential complexity). |
| Nested Loops (with Break): | O(n*m) | k nested loops, each iterating n times, with early termination (quadratic complexity). |
| Do-While Loop: | O(n) | Similar to a while loop, but guarantees at least one iteration (linear complexity). |
| Recursion: | Varies (e.g., O(2^n), O(n!)) | Depends on the recursive algorithm and branching factor. |
| Binary Search: | O(log n) | Reduces the search space by half in each iteration (logarithmic complexity). |
| For each Loop: | O(n) | Iterates over all elements in a collection (linear complexity). |
To wrap it ip:
Understanding the time complexity of recursive loops is fundamental for programmers to develop efficient algorithms.
By grasping the factors influencing time complexity and employing optimization techniques, developers can create faster and more scalable code.
FAQs
The time complexity depends on how many times the function calls itself and the amount of work done in each call. It’s often expressed using recurrence relations like T(n) = T(n-1) + O(1).
Recursive functions may have higher time and space complexity due to repeated calls and stack usage. Iteration avoids overhead by using loops without additional stack frames.
You can use recurrence relations and solve them using methods like the recursion tree or master theorem. Analyzing the number of calls and work per call is key.
Yes, Python’s recursion depth is limited, and excessive recursion can lead to stack overflow or performance issues. Optimized recursive algorithms or iteration is preferred for large inputs.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others







Login/Signup to comment