Searching in Binary Search Tree

September 30, 2023

searching BST

Introduction to Searching in BST

Binary Search Trees (BSTs) stand out as efficient and organized repositories of information. These hierarchical structures are designed to facilitate rapid data retrieval, and one of their primary strengths lies in their search capabilities.

In this article, you will get to know learn about Searching in binary Search Tree, Conditions and methods.  

What is Binary Search Tree(BST)?

A Binary Search Tree (BST) is a hierarchical data structure used for organizing and storing data in a way that allows for efficient searching, insertion, and deletion of elements.

Conditions for Searching in Binary Search Tree:

The basic idea behind searching in Binary Search Tree is to leverage the ordering property of the tree:

  1. All nodes in the left subtree of a node have values less than or equal to the node’s value.
  2. All nodes in the right subtree of a node have values greater than or equal to the node’s value.
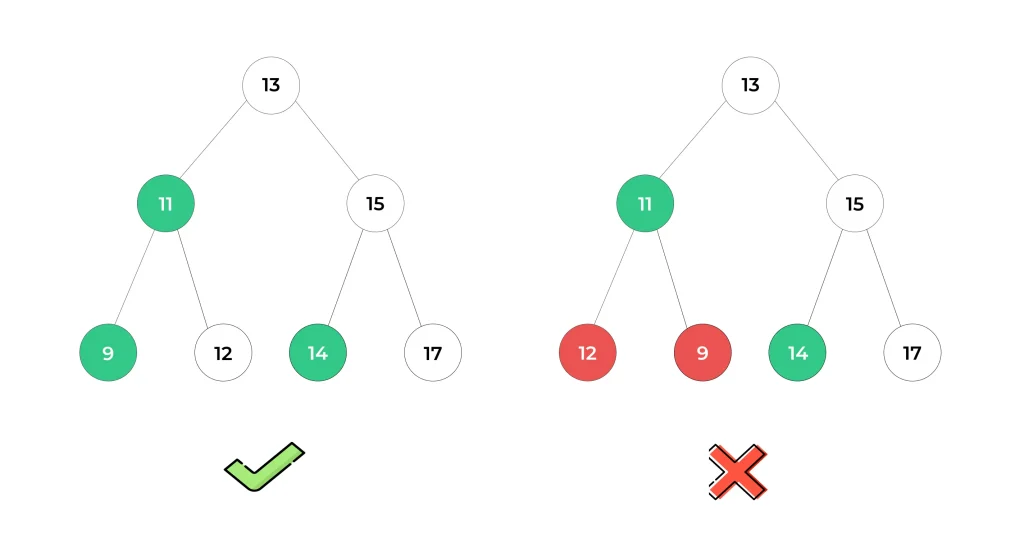
Binary Search Tree

 

Search Operation for Binary Search Tree(BST)

Searching in Binary Search Tree (BST) is an essential operation that takes advantage of the tree’s hierarchical and ordered structure. The goal is to efficiently find a specific element (or key) within the BST.

Let us visualize the searching operation in BST:

  1. Start at the Root:

    • The search operation begins at the root node of the BST, which is the topmost node.
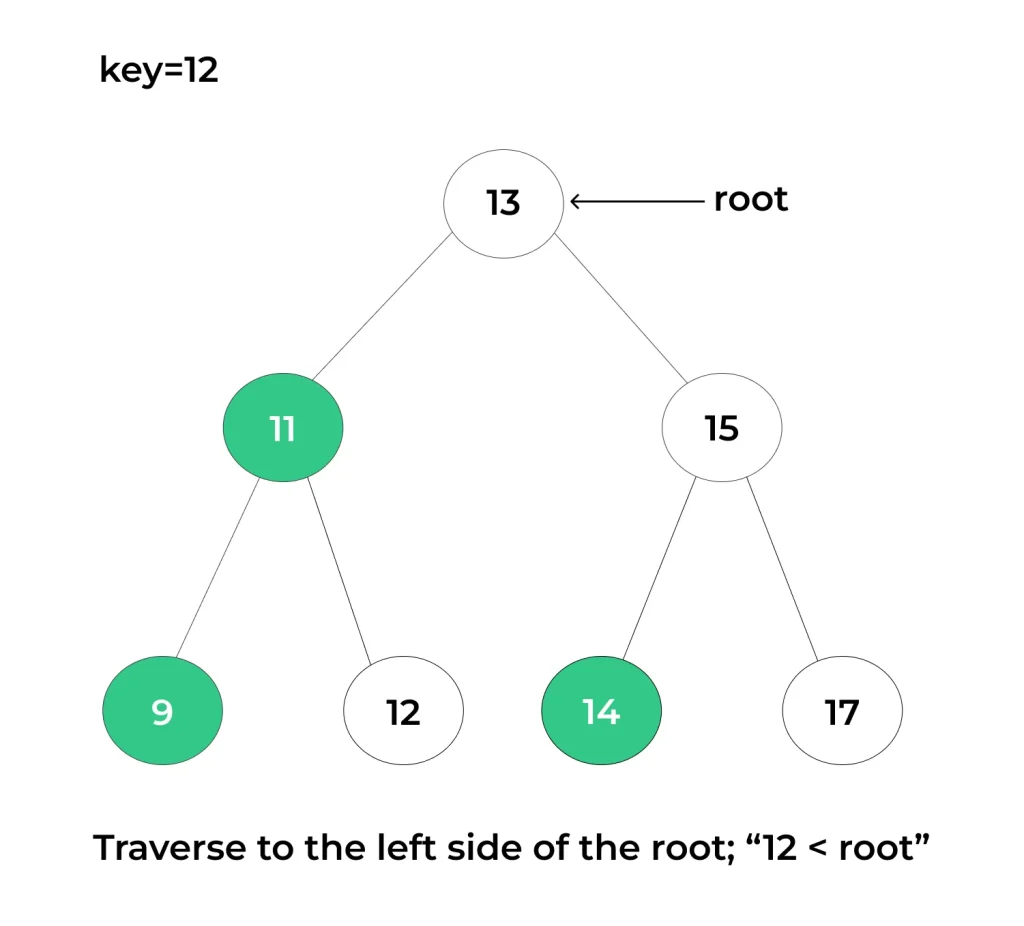
Search Binary Tree
  1. Compare with Current Node:
  • Compare the target key (the element you’re searching for) with the key of the current node.
  • There are three possible outcomes:
    • If the target key matches the key of the current node, the search operation is successful, and the current node is the result.
    • If the target key is less than the key of the current node, move to the left child node.
    • If the target key is greater than the key of the current node, move to the right child node.
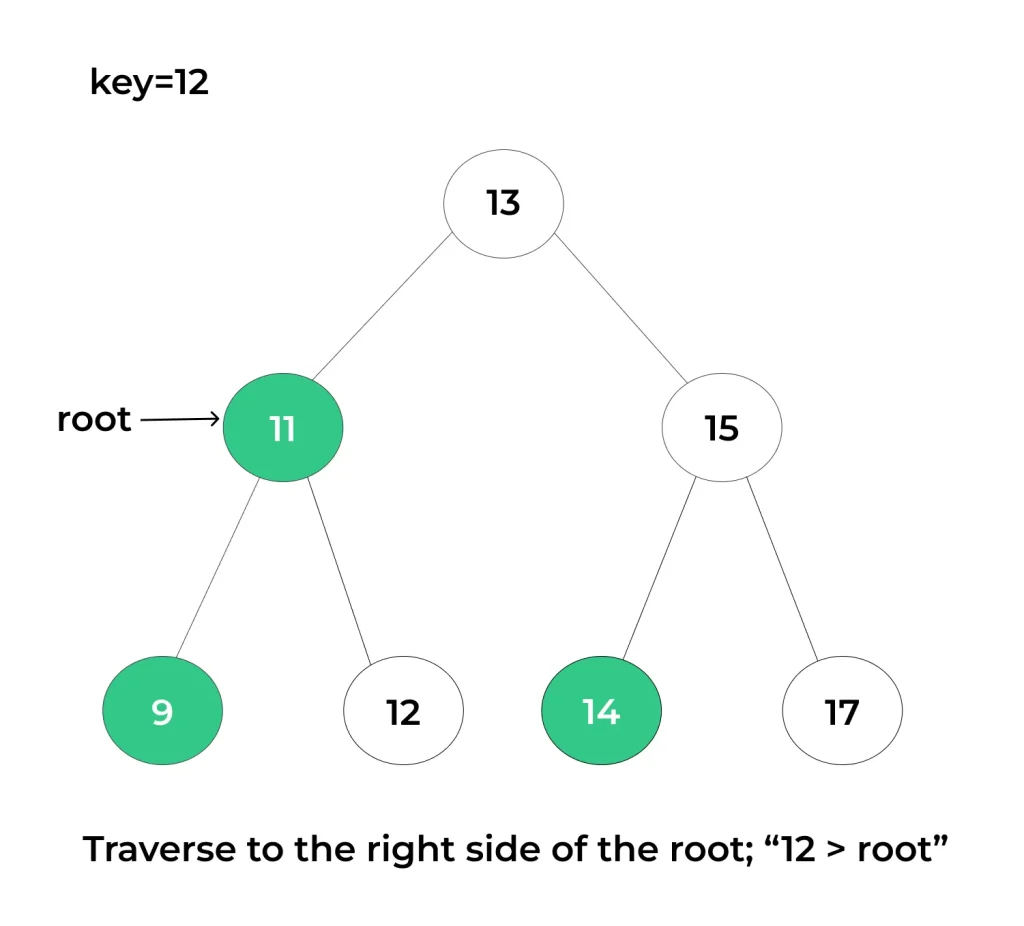
Search Binary tree 2
  1. Repeat Until Found or Null:
  • Continue comparing the target key with the key of the current node, and based on the comparison result, move to the left or right subtree.
  • If you encounter a null (empty) node while traversing (i.e., there are no more nodes to explore in that direction), it means the target key is not present in the BST, and the search operation terminates.
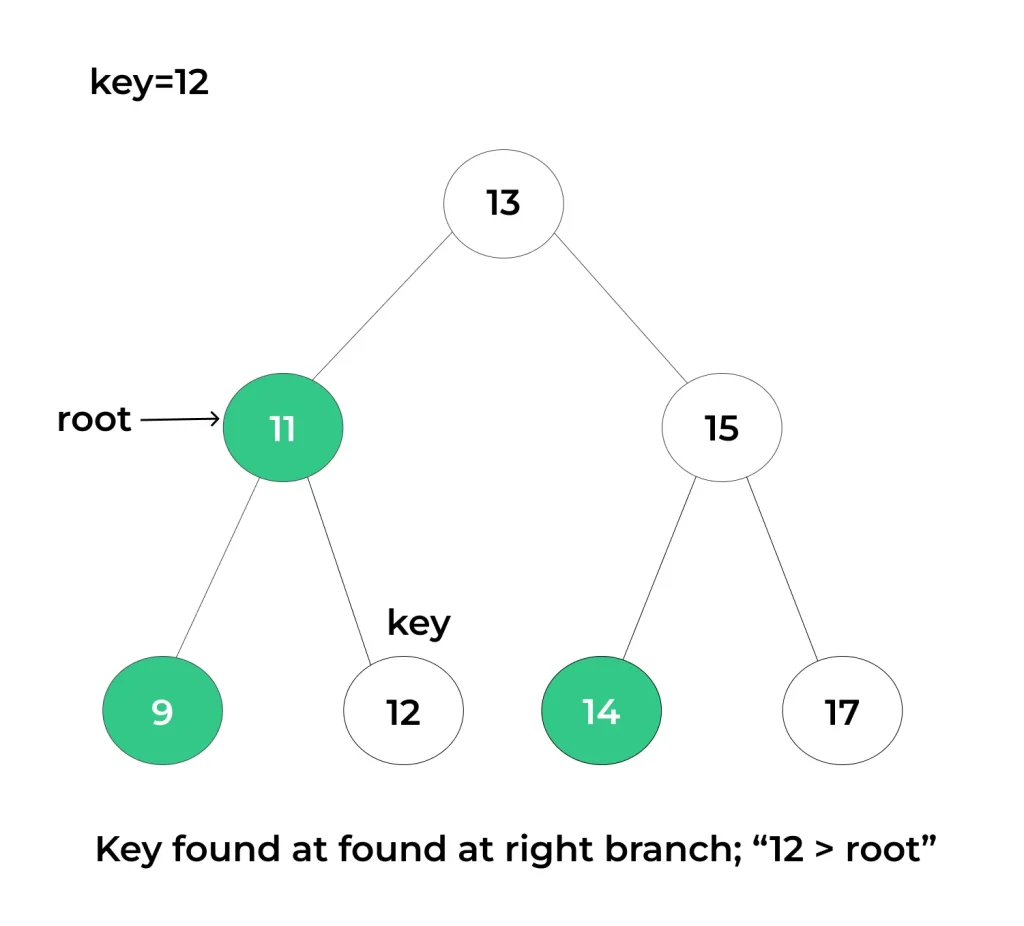
Search Binary tree 3
  1. Termination and Result:
  • The search operation terminates when one of the following conditions is met:
    • The target key is found in the BST, and the node containing that key is the result.
    • A null (empty) node is reached, indicating that the target key is not present in the BST.
  • At this point, you can return the result (the node containing the target key) or indicate that the key is not in the BST.

Methods of Searching in Binary Search Tree(BST)

There are mainly two methods for Searching in Binary Search Tree:

  1. Recursive Method

  2. Iterative Method

Searching in Binary Search Tree(BST) using Recursive method
class TreeNode:
    def __init__(self, key):
        self.val = key
        self.left = None
        self.right = None

def search_bst(root, key):
    
    if root is None or root.val == key:
        return root

   
    if key < root.val:
        return search_bst(root.left, key)
    
    else:
        return search_bst(root.right, key)

if __name__ == "__main__":
    root = TreeNode(50)
    root.left = TreeNode(30)
    root.right = TreeNode(70)
    root.left.left = TreeNode(20)
    root.left.right = TreeNode(40)
    root.right.left = TreeNode(60)
    root.right.right = TreeNode(80)

    # Search for a key (e.g., 40) in the BST:
    target_key = 40
    result_node = search_bst(root, target_key)

    if result_node:
        print("Key", target_key, "found in the BST.")
    else:
        print("Key", target_key, "not found in the BST.")

Output :

Key 40 found in the BST.
Explanation

The code demonstrates a recursive search operation in a Binary Search Tree (BST).

  • It defines a TreeNode class to create BST nodes and a search_bst function to find a specified key.
  • The search starts from the root, recursively moving left or right based on comparisons until the key is found or determined as absent.
  • The result is printed, indicating whether the key was found in the BST.

Searching in Binary Search Tree(BST) using Iterative method
class TreeNode:
    def __init__(self, key):
        self.key = key
        self.left = None
        self.right = None

def search_iterative(root, key):
    current = root

    while current:
        if key == current.key:
            return True  # Key found in the BST
        elif key < current.key:
            current = current.left  # Traverse left subtree
        else:
            current = current.right  # Traverse right subtree

    return False  # Key not found in the BST

# Example usage:
if __name__ == "__main__":
    root = TreeNode(50)
    root.left = TreeNode(30)
    root.right = TreeNode(70)
    root.left.left = TreeNode(20)
    root.left.right = TreeNode(40)
    root.right.left = TreeNode(60)
    root.right.right = TreeNode(80)

    key_to_search = 40
    if search_iterative(root, key_to_search):
        print("Key", key_to_search, "found in the BST.")
    else:
        print("Key", key_to_search, "not found in the BST.")

Output :

Key 40 found in the BST.
Explanation

This code implements an iterative search for a key in a Binary Search Tree (BST). It starts at the root and traverses the tree, comparing the key with the current node’s key. If a match is found, it returns True. The absence of the key results in a False return. In the example, it successfully searches for the key 40 and indicates its presence in the BST.

Algorithm for Binary Search Tree(BST) 

If node == NULL 
    return createNode(data)
if (data < node->data)
    node->left  = insert(node->left, data);
else if (data > node->data)
    node->right = insert(node->right, data);  
return node;
Time Complexity for Binary Search Tree

The time complexity for searching in a Binary Search Tree (BST) is primarily determined by the height of the tree and can vary based on whether the tree is balanced or unbalanced.

  1. Balanced BST:

    • Average Time Complexity: O(log n)
    • In a balanced BST, where the tree is structured in a way that ensures relatively equal left and right subtrees, the average time complexity for searching is logarithmic in the number of nodes (n). This is because with each comparison, you effectively reduce the search space by half.

  2. Unbalanced BST:

    • Worst-case Time Complexity: O(n)
    • In the worst case, when the BST is highly unbalanced and resembles a linked list, the time complexity for searching can be linear in the number of nodes (n). This occurs when the tree is not balanced, and you essentially have to traverse all nodes from the root to the target node.
Space Complexity for Binary Search Tree

The space complexity for searching in a Binary Search Tree (BST) primarily depends on the space used by the recursive function calls in the call stack during the search process. Here are the space complexity considerations:

  1. Recursive Search:

    • During a recursive search in a BST, the space complexity is determined by the maximum depth of the call stack, which corresponds to the height of the tree.
    • In a balanced BST, the height is logarithmic in the number of nodes (O(log n)), resulting in a space complexity of O(log n).
    • In an unbalanced BST (worst case), the height can be linear in the number of nodes (O(n)), leading to a space complexity of O(n).

  2. Auxiliary Space:

    • Apart from the recursive call stack, the space complexity for searching in a BST typically doesn’t involve significant additional auxiliary space.
    • The storage for local variables and the recursive call stack is the primary contributor to space complexity.
To wrap it up:

In conclusion, understanding the process of searching in a Binary Search Tree (BST) is essential for harnessing the efficiency of this data structure.

  • Whether in a balanced or unbalanced state, a BST’s hierarchical organization and ordered properties make searching a powerful operation.

Analysis of Algorithm

Searching in Python

Sorting Algorithm in Python

Trie in Python

Making a Trie Node Class

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Question 1.

How does searching in a BST differ from linear search in an array?

Searching in a BST has an average time complexity of O(log n), which is more efficient than linear search in an array with a time complexity of O(n) for unordered data.

Question 2.

What happens if the target key is not found in the BST?

If the target key is not found in the BST, the search process will continue until it reaches a null (empty) node. At that point, it’s determined that the key is not present in the BST.

Question 3.

What is the time complexity of searching in a BST?

In a balanced BST, the average time complexity for searching is O(log n), where n is the number of nodes. In the worst case, when the tree is highly unbalanced, it can be O(n).

Question 4.

Why are Binary Search Trees (BSTs) useful for searching?

BSTs are organized in a way that allows for efficient searching, with an average time complexity of O(log n) in balanced trees. This makes them suitable for tasks that require ordered data retrieval.

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout