Recursion and PMI
Introduction
Recursion and PMI (Principle of Mathematical Induction) are fundamental concepts in computer science and mathematics. In this page, we will explore how recursion is related to PMI and how these concepts are applied in Python programming.
Recursion is a powerful and elegant way to solve complex problems by breaking them down into smaller, more manageable subproblems.
Relation Between Recursion and PMI
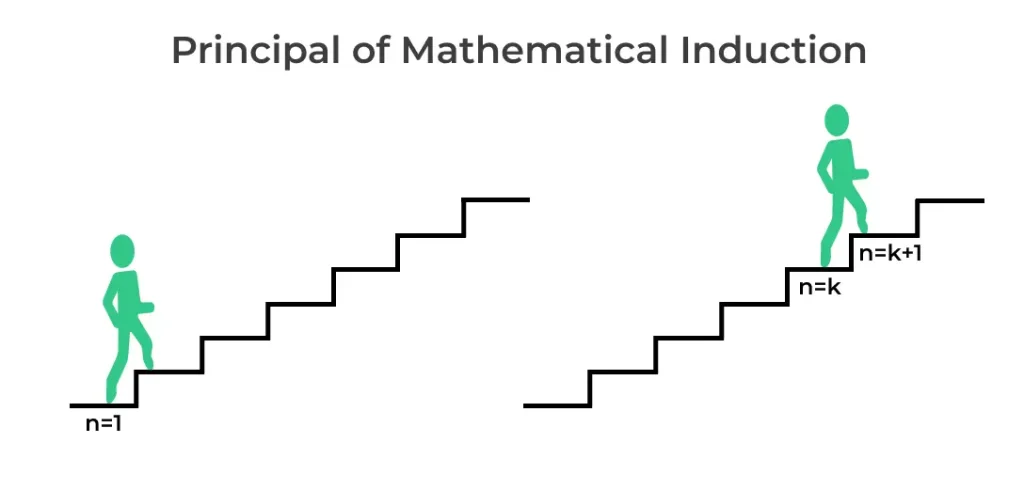
The Principle of Mathematical Induction (PMI) is a mathematical proof technique used to prove statements about natural numbers.
PMI has a close relationship with recursion because it often involves breaking down a problem into smaller cases and proving that the statement holds for the base case and any arbitrary case assuming it holds for the previous case.
PMI consists of three main steps:
Visualization of PMI
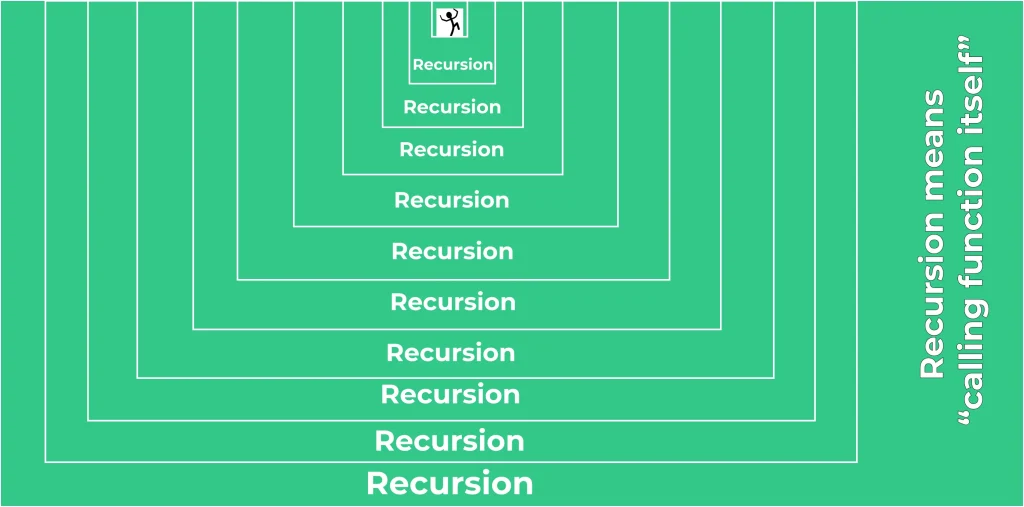
Visualization of Recursion
When you cannot put a stop condition (also known as a base case) in a recursive function, it leads to what is commonly referred to as “infinite recursion” or “recursion without termination.
” Infinite recursion occurs when the recursive function keeps calling itself indefinitely without reaching a base case that allows it to stop.
PMI and Recursive Algorithms
Recursive algorithms often follow the same structure as PMI proofs. The base case corresponds to the simplest subproblem that can be solved directly. The inductive hypothesis is analogous to assuming that the algorithm works for a smaller subproblem, and the inductive step is where the algorithm combines the solution for the smaller subproblem to solve the larger one.
Example: Fibonacci Series
The Fibonacci sequence is a classic example that demonstrates the relationship between recursion and PMI. The sequence is defined as follows:
F(0) = 0 F(1) = 1 F(n) = F(n-1) + F(n-2) for n > 1
This definition directly mirrors the PMI structure. The base cases are F(0) and F(1), the inductive hypothesis assumes that F(k) and F(k-1) are known, and the inductive step combines these to calculate F(k+1).
Here’s a Python implementation of the Fibonacci sequence using recursion:
In this implementation, the base cases (n=0 and n=1) are explicitly defined, and the inductive step is implemented through recursive function calls.
def fibonacci(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fibonacci(n-1) + fibonacci(n-2)
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Applications of Recursion and PMI
Recursion and the Principle of Mathematical Induction (PMI) have diverse applications in various fields. Here are some common applications of both recursion and PMI:
Applications of Recursion :
Algorithm Design: Many algorithms are naturally expressed using recursion, such as tree traversal algorithms (e.g., in binary search trees or decision trees) and graph traversal algorithms (e.g., depth-first search and breadth-first search).
Mathematical Calculations: Recursive functions are frequently used to compute mathematical series (e.g., Fibonacci sequence) and solve mathematical problems (e.g., calculating factorials or combinations).
Data Structures: Recursion is used to define and manipulate complex data structures, like recursive linked lists, trees, and graphs. Recursive definitions help simplify operations on these structures.
Applications of PMI :
Mathematical Proofs: PMI is a powerful technique for proving mathematical statements involving natural numbers. It is used to prove a wide range of mathematical theorems, including those related to number theory, sequences, and series.
Summation Formulas: PMI is used to derive summation formulas for arithmetic and geometric series, as well as other types of mathematical sequences.
Inequality Proofs: PMI can be applied to prove various inequalities, such as those related to the binomial coefficients, using induction.
Counting Problems: PMI is used to count and prove combinatorial results, especially in combinatorics and discrete mathematics.
To Wrap up with:
Recursion and PMI are powerful tools that help you to design and analyze recursive algorithms effectively. Python, with its support for recursive functions, provides a practical platform for implementing and experimenting with these concepts.
Whether you’re solving complex problems or proving mathematical theorems, the synergy between recursion and PMI is a valuable asset in your toolkit.
FAQs
Recursion and PMI are closely related, as both rely on breaking a problem into a base case and a smaller version of the same problem. Recursion solves problems step-by-step, while PMI proves correctness step-by-step.
The base case acts as a stopping condition in recursion and a starting point in PMI. Without it, both recursive functions and inductive proofs can lead to infinite loops or incomplete logic.
Yes, most well-defined recursive algorithms can be proven correct using PMI. PMI validates that the algorithm works for the base case and all subsequent cases through induction.
The inductive step assumes correctness for ‘n’ and proves for ‘n+1’, just like recursion solves ‘n’ by calling itself for ‘n-1’. This reflects a strong logical parallel between programming and mathematical proof.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others