Quadratic Probing in Hashing
Introduction to Quadratic Probing in Hashing
Hashing allows us to store and access data in a way that minimizes the time required to search for a specific element in a large dataset. One common method used in hashing is Quadratic Probing.
Lets explore more about Quadratic Probing in Hashing the depths of Quadratic Probing, exploring its mechanics, advantages, disadvantages, and real-world applications.
Exploring Quadratic Probing in Hashing
Quadratic probing is a method to resolve collisions that can occur during the insertion of data into a hash table. When a collision takes place (two keys hashing to the same location), quadratic probing calculates a new position by adding successive squares of an incrementing value (usually starting from 1) to the original position until an empty slot is found.
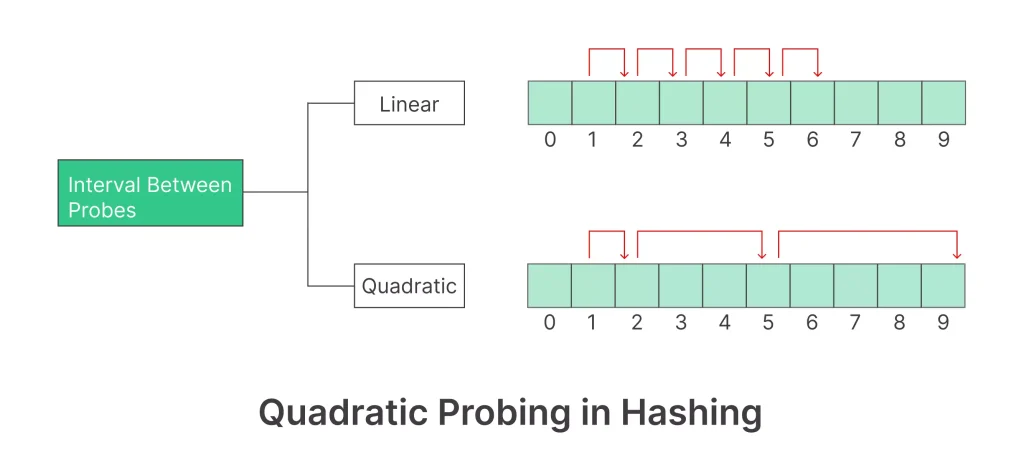
How Quadratic Probing Works
Quadratic Probing, as the name suggests, uses a quadratic function to resolve collisions. When a collision occurs (i.e., when the desired slot is already occupied), Quadratic Probing calculates the next available slot using a formula like (hash(key) + i^2) % table_size, where i is the number of probing attempts. This ensures a more even distribution of data in the hash table.
How Quadratic Probing Works
Quadratic probing involves three main steps:
- Calculate the initial hash position for the key.
- If the position is occupied, apply the quadratic probing formula to find the next available slot.
- Repeat this process until an empty slot is found, and insert the data.
New Position = (Initial Position + C1 * i + C2 * i^2) % Table Size
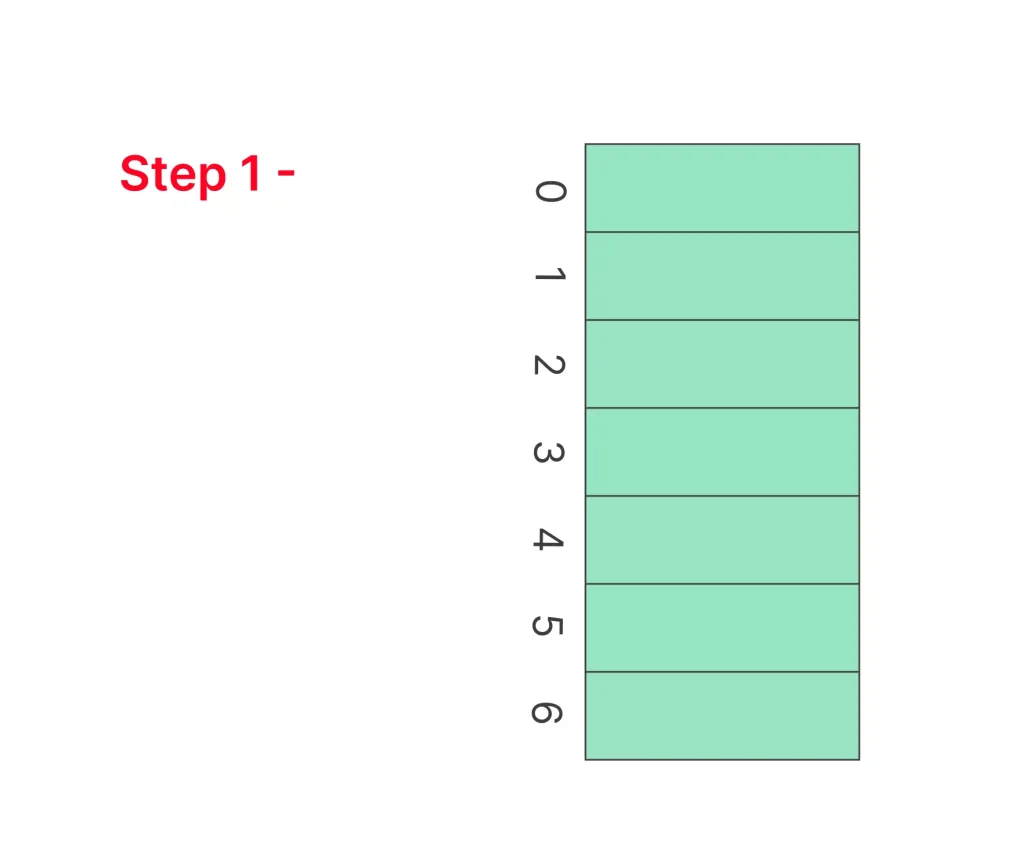
Example of Quadratic Probing in Hashing
Table size = 7 Insert = 15,22, 89 , Search & Delete = 85 , Hash Function –
Hash(x)=x%7 Collision Resolution Strategy f(i)= i^2
Step 1 – Create a table of size 7
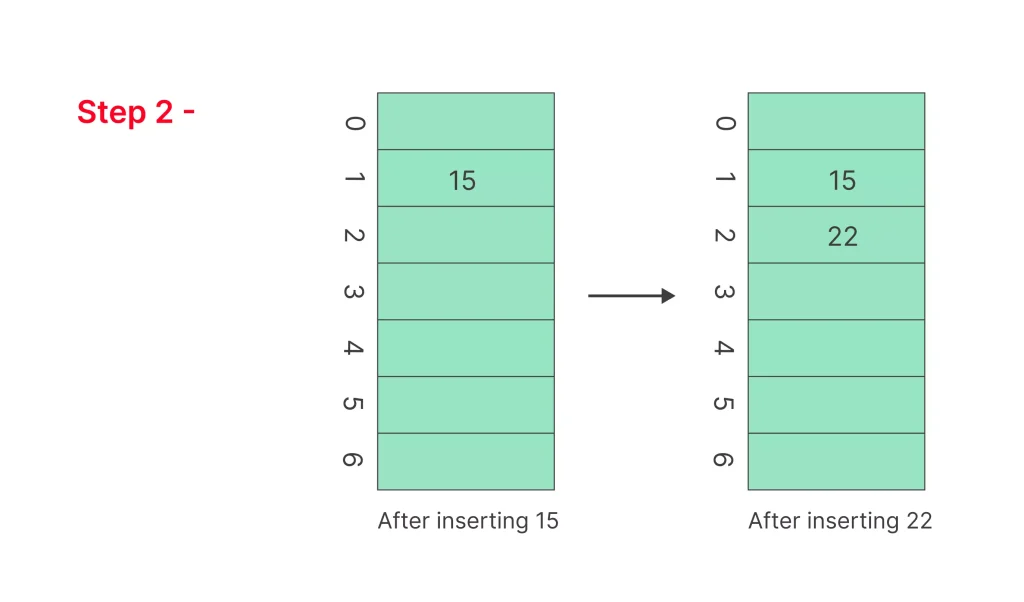
Step 2 -Insert 15, 22
- hash(15) = 15%7 = 1 cell at index 1 is not occupied we can insert cell in index 1.
- hash(22) = 22%7 = 2 Again cell is not occupied so place cell in index 2.
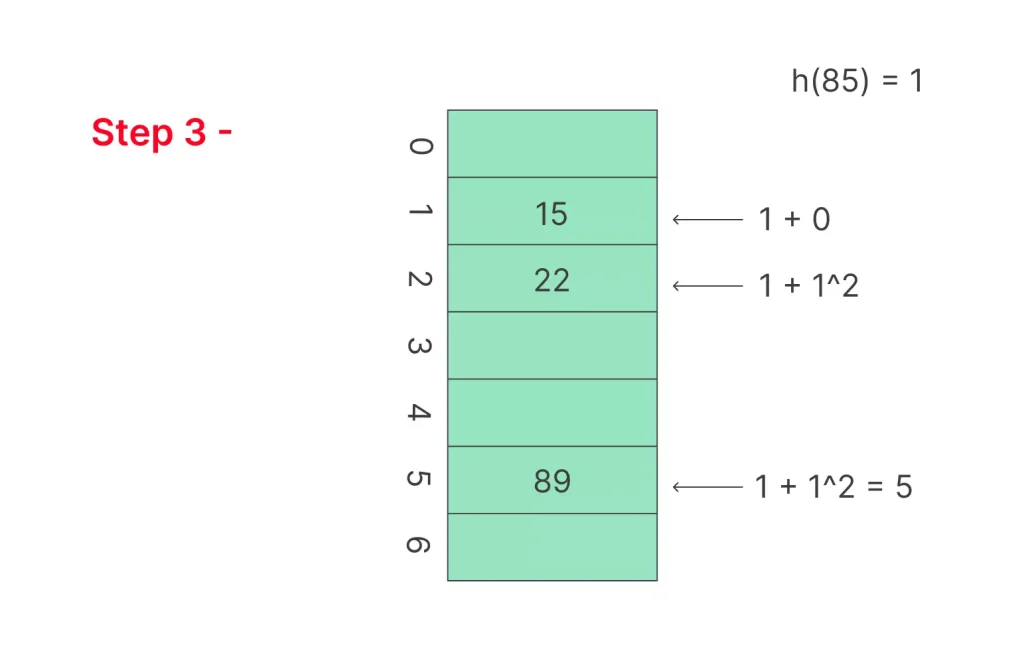
Step 3 – Inserting 85
- hash(85) = 85%7 = 1 , Since cell 1 is already occupied So we will search for the equation :
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Implementing Quadratic Probing in Hashing
class QuadraticProbingHashTable:
def __init__(self, size):
self.size = size
self.table = [None] * size
def hash_function(self, key):
return key % self.size
def insert(self, key):
index = self.hash_function(key)
i = 1
while self.table[index] is not None:
print(f"Collision at index {index}, trying quadratic probing...")
index = (self.hash_function(key) + i * i) % self.size
i += 1
if i == self.size:
print("Hash table is full")
return
self.table[index] = key
def display(self):
for i in range(self.size):
print(f"Index {i} --> {self.table[i]}")
# Example usage
hash_table = QuadraticProbingHashTable(7)
keys = [10, 20, 5, 15, 7]
for key in keys:
hash_table.insert(key)
hash_table.display()
Output:
Collision at index 6, trying quadratic probing... Collision at index 6, trying quadratic probing... Index 0 --> 7 Index 1 --> None Index 2 --> 16 Index 3 --> None Index 4 --> None Index 5 --> 5 Index 6 --> 10
Explanation:
- Quadratic Probing handles collisions by checking slots at increasing quadratic intervals: (hash + i²) % size.
- It reduces primary clustering, offering better distribution than linear probing.
- The probing sequence spreads entries further apart, helping avoid large clusters.
- It requires the hash table size to be appropriately chosen (often a prime) to ensure all slots can be probed.
- It continues probing until an empty slot is found or the table is declared full.
Time and Space Complexity :
| Operation | Complexity |
|---|---|
| Time Complexity | O(1) to O(n) |
| Space Complexity | O(n) |
Comparing Quadratic Probing with Other Techniques
Linear Probing vs. Quadratic Probing
While Linear Probing is straightforward, Quadratic Probing offers better performance due to its reduced clustering. However, Quadratic Probing may consume more memory.
Quadratic Probing vs. Double Hashing
Double Hashing is even more efficient than Quadratic Probing but can be more complex to implement. Quadratic Probing strikes a balance between simplicity and performance.
Pros and Cons of Quadratic Probing in Hashing
Pros of Quadratic Probing
Cons of Quadratic Probing
Applications of Quadratic Probing in Hashing
Quadratic probing is widely used in scenarios where quick data retrieval is crucial. Some common applications include:
Final Thoughts:
Quadratic Probing in Hashing emerges as a reliable technique to reduce clustering and enhance data retrieval efficiency. While it may not be the perfect solution for every scenario, it strikes a balance between simplicity and performance, making it a valuable tool in the world of data structures and algorithms.
FAQs
Quadratic probing is a collision resolution technique in open addressing where the interval between probes increases quadratically (e.g., 1², 2², 3², …). It reduces clustering issues compared to linear probing.
By using a quadratic function to determine the probe sequence, it spreads out entries more evenly. This avoids primary clustering common in linear probing.
The formula is: (hash(key) + i²) % table_size, where i is the probe number. It ensures that the next position is checked based on a quadratic distance.
Quadratic probing may not examine all slots in the hash table unless the table size is prime. It can also fail to insert even when free slots exist if the probing sequence misses them.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others




Login/Signup to comment