Preorder Traversal of Binary Tree
Introduction to Preorder Traversal of Binary Traversal
Preorder traversal of Binary Tree is one of the fundamental techniques used to explore and manipulate binary trees, a data structure widely used in computer science and programming. This technique allows you to visit each node in a binary tree systematically, making it an essential tool for a variety of tasks like searching, insertion, and deletion.
Let’s learn more about Preorder Traversal of Binary Tree along with its working and implementation.
Methods of Tree Traversal
There are three primary methods of tree traversal:
- Preorder Traversal
- Postorder Traversal
- Inorder Traversal
In this article, we are going to explore more about Preorder Traversal of Binary Tree.
Tree Traversal in Data Structure Examples
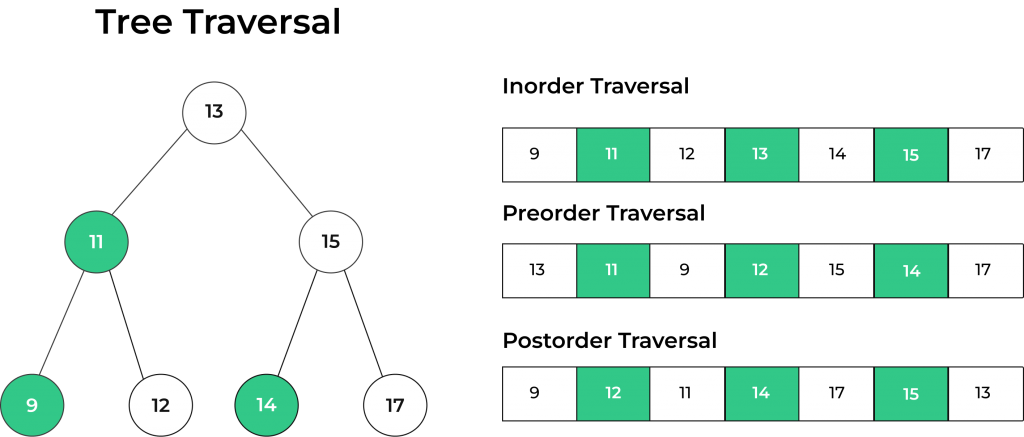
Preorder Traversal of Binary Tree
Preorder traversal, also known as DLR (Data-Left-Right) traversal, is a depth-first traversal technique for binary trees. The name “preorder” signifies the order in which you visit the nodes of the tree. In preorder traversal, you start at the root node, then traverse the left subtree, and finally explore the right subtree.
Visualization of Preorder Traversal
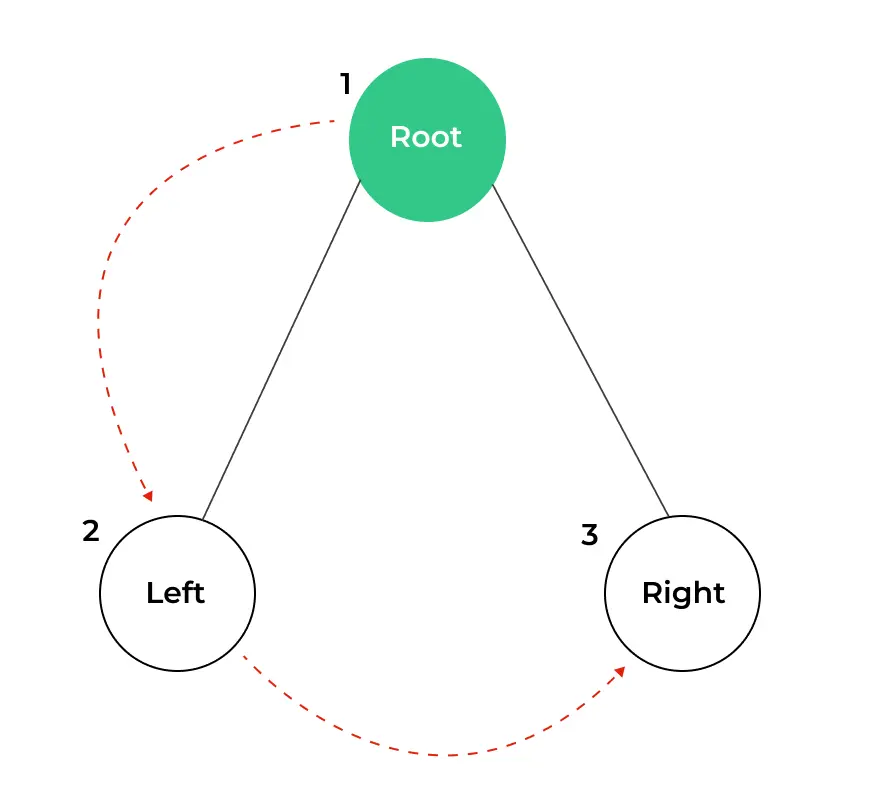
Working of Preorder Traversal
Consider a binary tree :
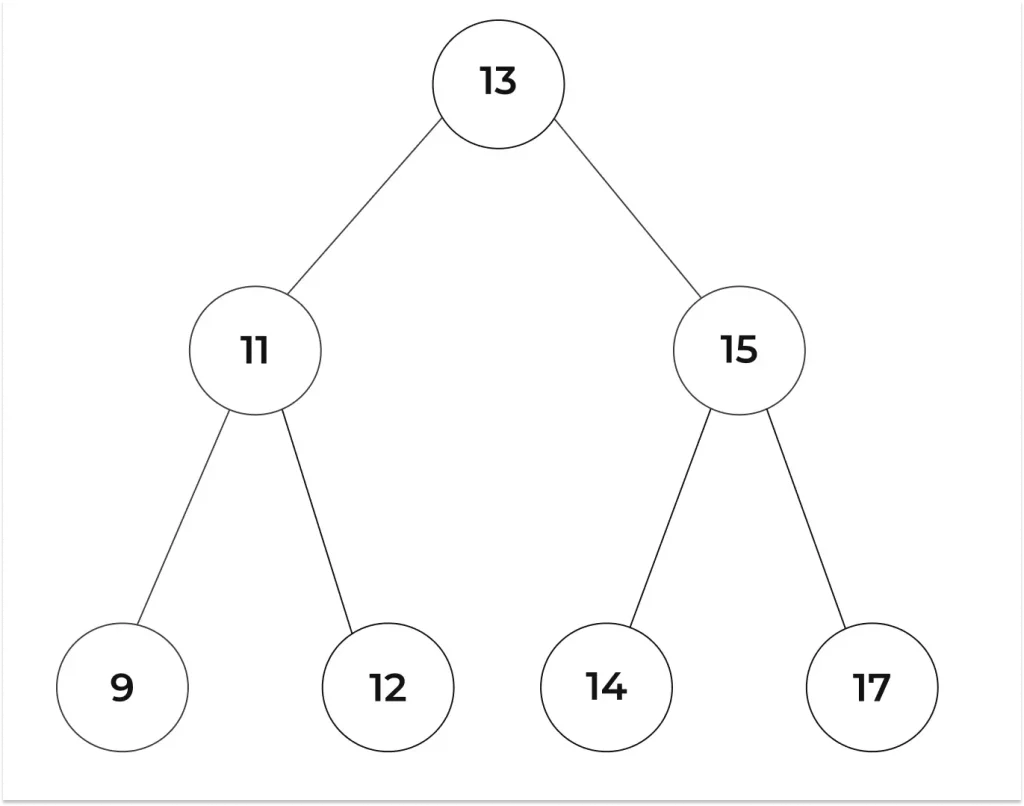
When conducting a preorder traversal within this binary tree, the sequence of steps unfolds as follows:
Step 1 : The initial visitation targets the root, denoted as node 13.
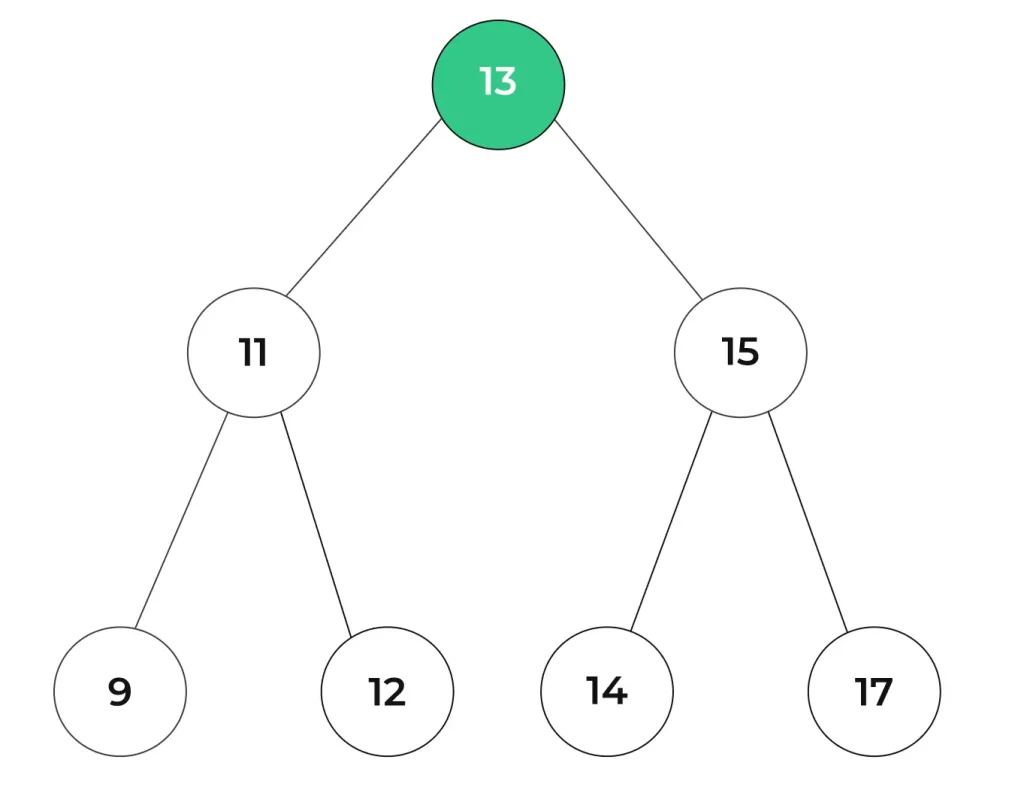
Step 2 : Subsequently, we proceed to explore the left subtree, leading to the visitation of the left subtree’s root, namely node 11.
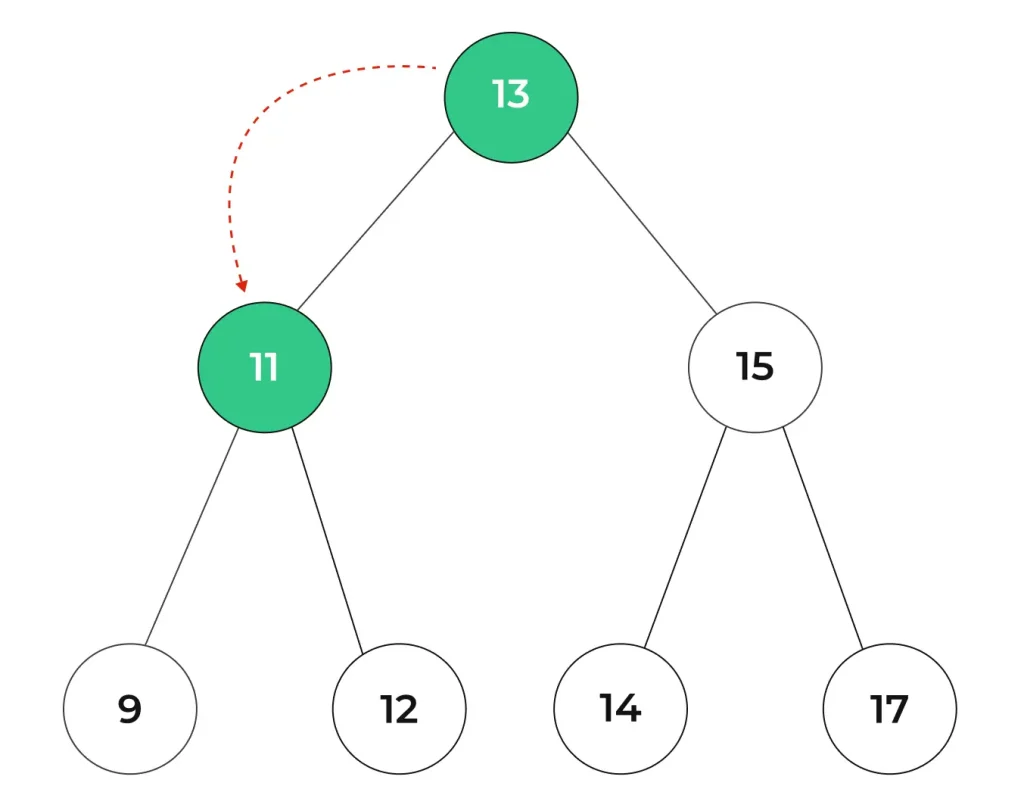
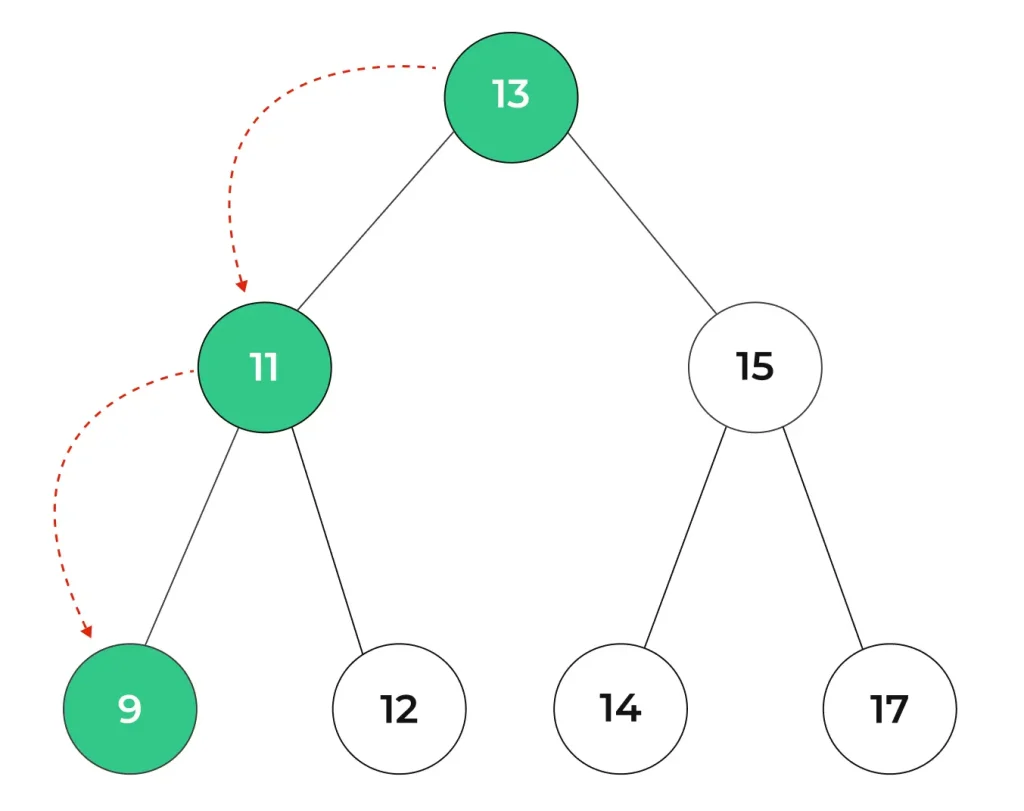
Step 3 : Again we have to traverse through the left sub-tree of node 11 i.e. node 9.
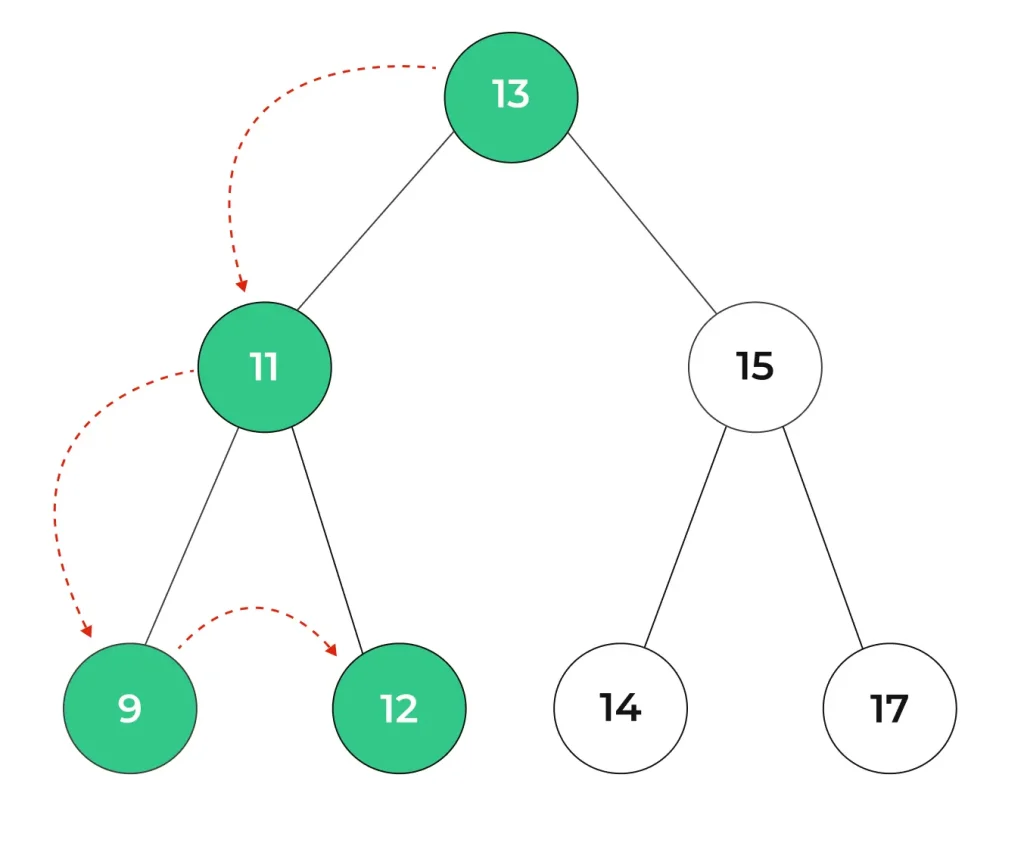
Step 4 : Now we have to move to the right sub-tree of the node 11 i.e. node 12.
Step 5 : The left sub-tree of node 13 is traversed. Now we have to visit the right sub-tree of the node 13 i.e. node 15.
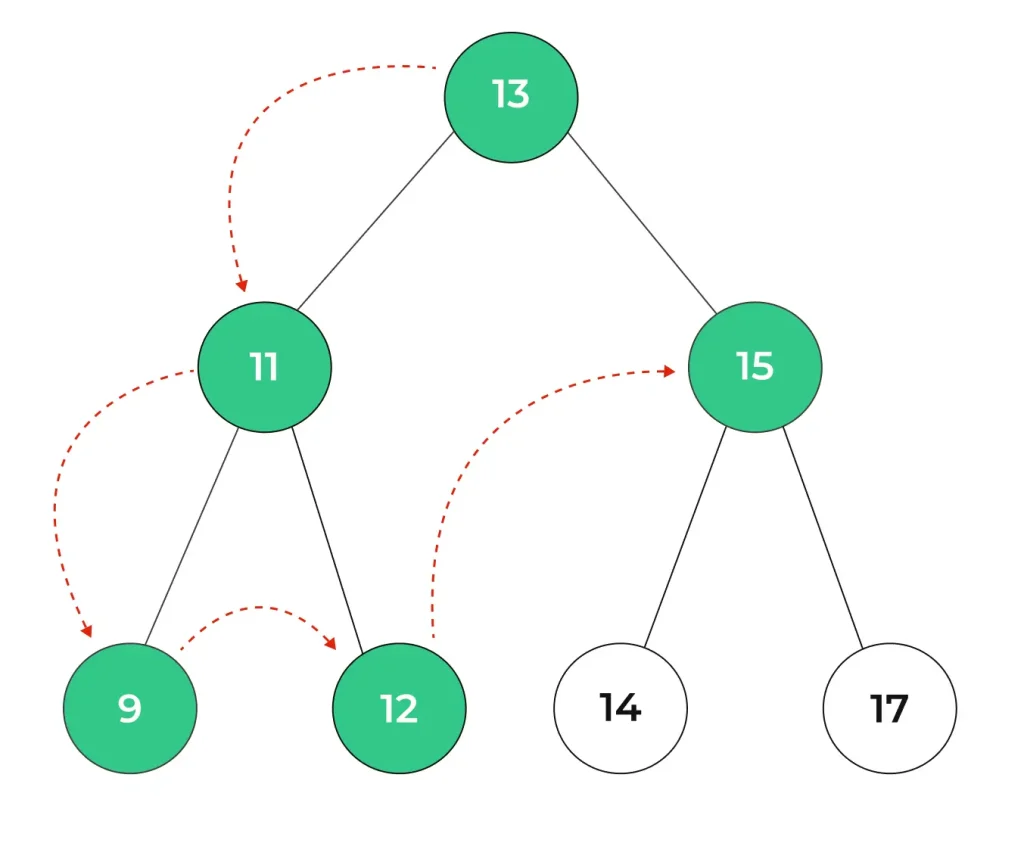
Step 6 : Now we have to traverse the left sub-tree of node 15 i.e. node 14.
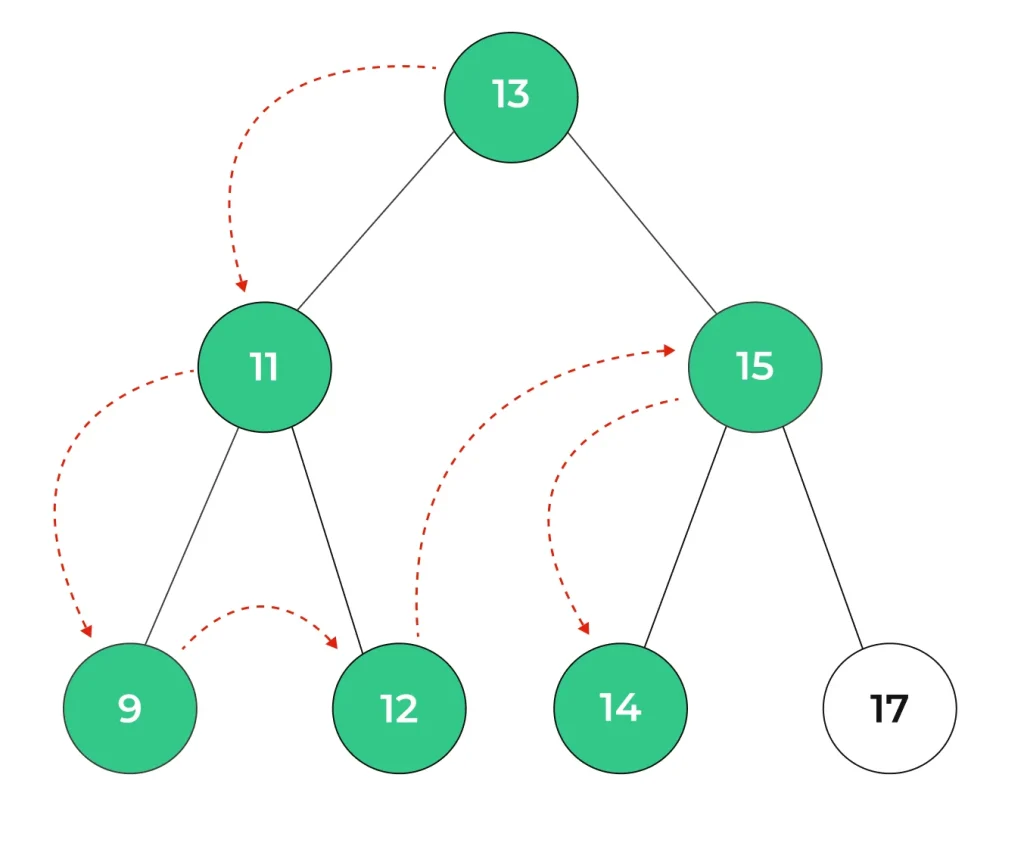
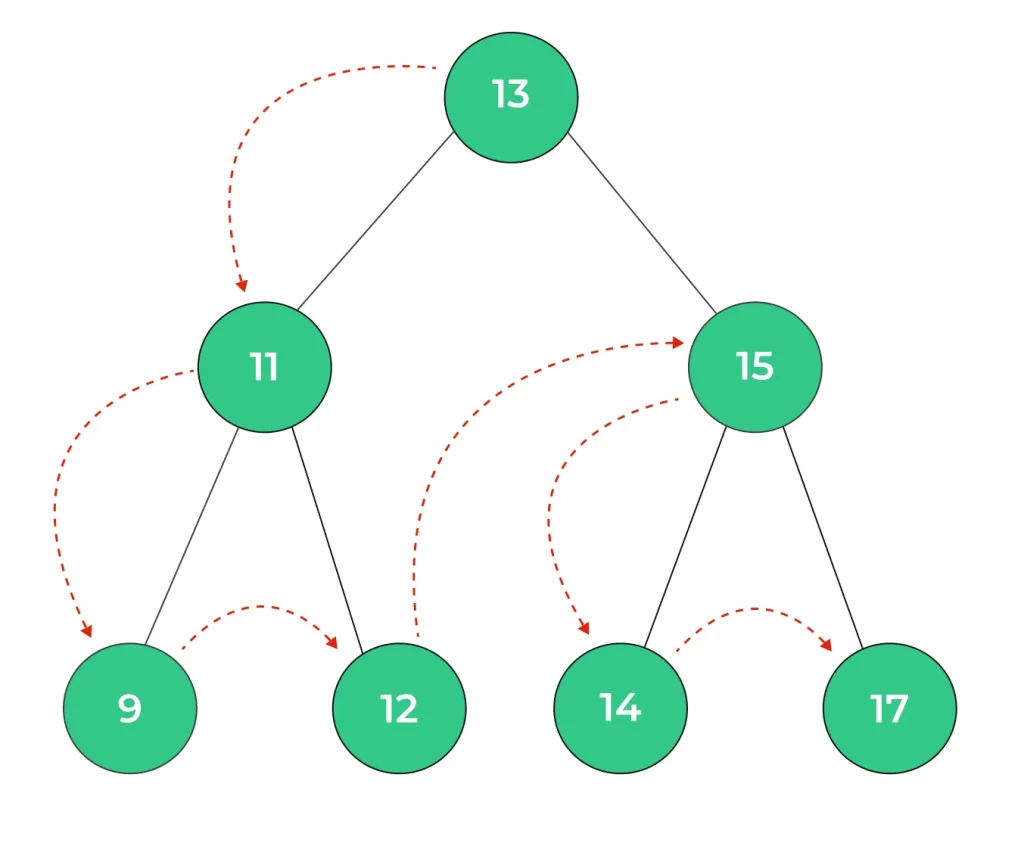
Step 7 : Traverse the right sub-tree of node 15 i.e. node 17.
Preorder Traversal using Recursive Method
Code :
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def recursive_preorder_traversal(node):
if node is not None:
# 1. Visit the current node
print(node.value)
# 2. Recursively traverse the left subtree
recursive_preorder_traversal(node.left)
# 3. Recursively traverse the right subtree
recursive_preorder_traversal(node.right)
Preorder Traversal using Iterative Method(Using Stack)
def iterative_preorder_traversal(root):
if root is None:
return
stack = [root]
while stack:
node = stack.pop()
# 1. Visit the current node
print(node.value)
# 2. Push the right child first (if it exists)
if node.right:
stack.append(node.right)
# 3. Push the left child (if it exists)
if node.left:
stack.append(node.left)
Preorder Traversal using Morris Method(Space-Efficient)
def morris_preorder_traversal(root):
current = root
while current is not None:
if current.left is None:
# 1. Visit the current node
print(current.value)
current = current.right
else:
# Find the rightmost node in the left subtree
predecessor = current.left
while (predecessor.right is not None) and (predecessor.right != current):
predecessor = predecessor.right
if predecessor.right is None:
# Make the threaded link from predecessor to the current node
predecessor.right = current
# 2. Visit the current node
print(current.value)
current = current.left
else:
# Remove the threaded link
predecessor.right = None
current = current.right
Complexity Analysis of Preorder Traversal
Applications of Tree Traversal in Data Structure
Tree traversal algorithms have a wide range of applications in computer science and real-world scenarios. Some common applications include:
To Wrap it up:
In conclusion, Whether you opt for the recursive, iterative (using a stack), or space-efficient Morris traversal method, mastering preorder traversal is essential for efficiently handling binary trees and a wide array of applications in computer science and programming. Understanding the concept and its applications is a valuable asset for developers and problem solvers dealing with tree structures.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Question 1.
Can Preorder Traversal be Implemented Recursively?
Yes, you can implement preorder traversal using a recursive approach. This involves defining a recursive function that visits the current node and recursively traverses the left and right subtrees.
Question 2.
Are There Non-Recursive Methods for Preorder Traversal?
Yes, you can use an iterative approach with a stack data structure to perform preorder traversal without recursion. Another method, known as Morris traversal, is a space-efficient non-recursive technique.
Question 3.
What’s the Time Complexity of Preorder Traversal?
The time complexity of preorder traversal is O(n), where ‘n’ is the number of nodes in the binary tree. This is because you need to visit each node exactly once.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
