Minimum Spanning Tree in Python
Introduction to MST
Minimum Spanning Tree is a connected, undirected graph is a subset that encompasses all the graph’s vertices while adhering to the characteristics of a tree. These algorithms help optimize network design, minimize costs, and enhance the efficiency of communication and transportation systems.
In the context of finding a MST, the goal is to find a spanning tree with the minimum possible total edge weight.
What is Spanning Tree?
A spanning tree in a connected, undirected graph is a subset that encompasses all the graph’s vertices while adhering to the characteristics of a tree.
- To put it differently, it is a tree structure that covers every vertex of the original graph without forming any cycles.
Here are some key characteristics of a spanning tree:
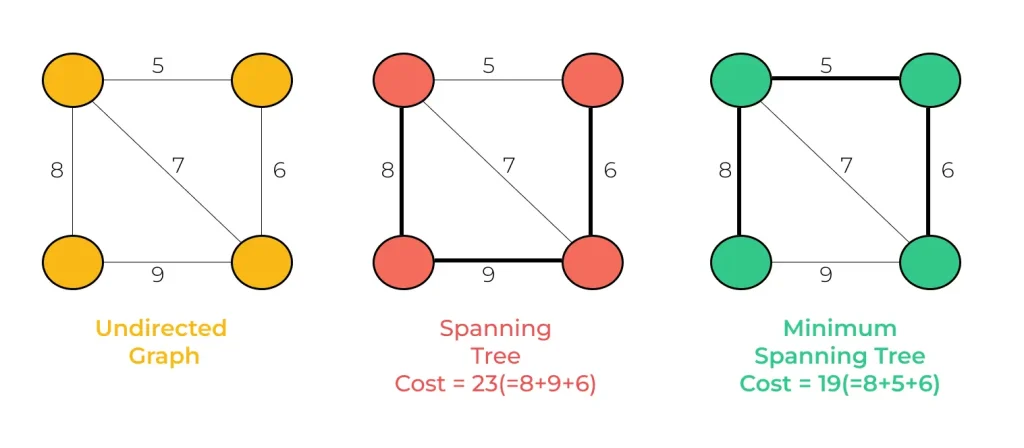
Minimum Spanning Tree
A MST is a type of tree, indicating it is a connected, acyclic graph. It guarantees the existence of a single path between any two vertices, with the absence of cycles or loops within its structure.
For Example :
Imagine a network of cities connected by roads, where each road has a certain distance associated with it. A Minimum Spanning Tree for this network would be the subset of roads that connects all cities with the shortest total distance possible.
Properties of Minimum Spanning Tree
Following are the properties of Minimum Spanning Trees(MST) :
- Removing any edge from the spanning tree results in its disconnection.
- The addition of an edge to the spanning tree introduces a loop.
- In a graph where each edge possesses a unique weight, there exists only one distinct MST. Conversely, if edge weights are not distinct, there may be multiple MST.
- A complete undirected graph can have a total of n^(n-2) spanning trees, where ‘n’ represents the number of vertices.
- Every connected and undirected graph contains at least one spanning tree.
- A disconnected graph does not possess any spanning tree.
- In a complete graph, the maximum number of edges that can be removed to construct a spanning tree is ‘e – n + 1′, where ‘e’ is the number of edges and ‘n’ is the number of vertices.
Key Characteristics of MST
Algorithms for Finding MST
Several algorithms can be employed to find the Minimum Spanning Tree of a graph, each with its own set of advantages and use cases. Some popular algorithms include:
Kruskal’s Algorithm: This algorithm grows the MST one edge at a time by selecting the smallest available edge that doesn’t create a cycle.
Prim’s Algorithm: Starting from an arbitrary vertex, this algorithm adds the shortest edge that connects a vertex outside the tree to the tree at each step.
Boruvka’s Algorithm: This algorithm works by adding the smallest edge for each component of the graph in each iteration.
1. Finding MST using Kruskal’s Algorithm
This implementation assumes that the graph is represented as an adjacency list, where each node is a tuple of the form (weight, u, v) indicating an edge between vertices u and v with weight weight.
Run
class DisjointSet:
def __init__(self, vertices):
self.parent = {vertex: vertex for vertex in vertices}
self.rank = {vertex: 0 for vertex in vertices}
def find(self, vertex):
if self.parent[vertex] != vertex:
self.parent[vertex] = self.find(self.parent[vertex])
return self.parent[vertex]
def union(self, root1, root2):
if self.rank[root1] > self.rank[root2]:
self.parent[root2] = root1
elif self.rank[root1] < self.rank[root2]:
self.parent[root1] = root2
else:
self.parent[root2] = root1
self.rank[root1] += 1
def kruskal(graph):
# Sort edges in ascending order of weight
edges = sorted(graph, key=lambda x: x[0])
vertices = set()
for edge in edges:
vertices.add(edge[1])
vertices.add(edge[2])
disjoint_set = DisjointSet(vertices)
minimum_spanning_tree = []
for edge in edges:
weight, u, v = edge
root1 = disjoint_set.find(u)
root2 = disjoint_set.find(v)
if root1 != root2:
minimum_spanning_tree.append(edge)
disjoint_set.union(root1, root2)
return minimum_spanning_tree
# Example usage:
graph = [
(1, 'A', 'B'),
(4, 'A', 'D'),
(3, 'B', 'D'),
(2, 'B', 'E'),
(5, 'D', 'E'),
(1, 'C', 'E')
]
result = kruskal(graph)
print("Minimum Spanning Tree:", result)
Output
[(1, 'A', 'B'), (1, 'C', 'E'), (2, 'B', 'E'), (3, 'B', 'D')]
2. Finding MST using Prim's Algorithm
Prim’s Algorithm is a greedy algorithm used to find the Minimum Spanning Tree (MST) of a connected, undirected weighted graph. An MST connects all the vertices in the graph with the minimum total edge weight and no cycles.
def prims_algorithm(graph, start_node):
visited = set()
min_heap = [(0, start_node)]
parent = {start_node: None}
mst_edges = []
total_weight = 0while min_heap:
weight, current_node = heapq.heappop(min_heap)
if current_node in visited:
continue
visited.add(current_node)
total_weight += weight
if parent[current_node] is not None:
mst_edges.append((parent[current_node], current_node, weight))
for neighbor, edge_weight in graph[current_node]:
if neighbor not in visited:
heapq.heappush(min_heap, (edge_weight, neighbor))
parent[neighbor] = current_node
return mst_edges, total_weight
# Sample graph (adjacency list)
graph = {
'A': [('B', 2), ('C', 3), ('D', 6)],
'B': [('A', 2), ('D', 1)],
'C': [('A', 3), ('D', 5)],
'D': [('A', 6), ('B', 1), ('C', 5)],
}
# Starting node for Prim's Algorithm
start_node = 'A'
# Run the algorithm
mst, total_cost = prims_algorithm(graph, start_node)
# Print the results
print("Minimum Spanning Tree (MST) edges:")
for u, v, w in mst:
print(f"{u} - {v} : {w}")
print(f"Total weight of MST: {total_cost}")
Output
Minimum Spanning Tree (MST) edges: A - B : 2 B - D : 1 A - C : 3 Total weight of MST: 6
3. Finding MST using Boruvka's Algorithm:
Borůvka’s Algorithm is a greedy algorithm for finding a Minimum Spanning Tree (MST) of a connected, weighted graph. It works by repeatedly adding the smallest edge from each component until all vertices are connected.
class Graph:
def __init__(self, vertices):
self.V = vertices
self.graph = []
def add_edge(self, u, v, w):
self.graph.append([u, v, w])
def find_parent(self, parent, i):
if parent[i] != i:
parent[i] = self.find_parent(parent, parent[i])
return parent[i]
def union(self, parent, rank, x, y):
xroot = self.find_parent(parent, x)
yroot = self.find_parent(parent, y)
if rank[xroot] < rank[yroot]: parent[xroot] = yroot elif rank[xroot] > rank[yroot]:
parent[yroot] = xroot
else:
parent[yroot] = xroot
rank[xroot] += 1
def boruvka_mst(self):
parent = []
rank = []
cheapest = [-1] * self.V
numTrees = self.V
MST_weight = 0
MST_edges = []
for node in range(self.V):
parent.append(node)
rank.append(0)
while numTrees > 1:
for i in range(len(self.graph)):
u, v, w = self.graph[i]
set1 = self.find_parent(parent, u)
set2 = self.find_parent(parent, v)
if set1 != set2:
if cheapest[set1] == -1 or cheapest[set1][2] > w:
cheapest[set1] = [u, v, w]
if cheapest[set2] == -1 or cheapest[set2][2] > w:
cheapest[set2] = [u, v, w]
for node in range(self.V):
if cheapest[node] != -1:
u, v, w = cheapest[node]
set1 = self.find_parent(parent, u)
set2 = self.find_parent(parent, v)
if set1 != set2:
MST_weight += w
MST_edges.append((u, v, w))
self.union(parent, rank, set1, set2)
numTrees -= 1
cheapest = [-1] * self.V
print("Edges in MST:")
for u, v, weight in MST_edges:
print(f"{u} -- {v} == {weight}")
print("Total weight of MST:", MST_weight)
# Example usage
g = Graph(4)
g.add_edge(0, 1, 10)
g.add_edge(0, 2, 6)
g.add_edge(0, 3, 5)
g.add_edge(1, 3, 15)
g.add_edge(2, 3, 4)
g.boruvka_mst()
Output
Edges in MST: 2 -- 3 == 4 0 -- 3 == 5 0 -- 1 == 10 Total weight of MST: 19
Application of Finding MST
An overview of different sets of applications for finding MST :
To Wrap it up:
Understanding and efficiently finding the Minimum Spanning Tree of a graph is essential in various fields. Whether optimizing network connections, designing transportation systems, or minimizing wire lengths in circuits, the concept of MST plays a pivotal role in creating efficient and cost-effective solutions.
Learn DSA
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
FAQs
A Minimum Spanning Tree in Python is a subset of edges in a weighted graph that connects all vertices with the minimum possible total edge weight. It can be implemented using algorithms like Kruskal’s or Prim’s.
To implement a Minimum Spanning Tree in Python, you can use libraries like NetworkX, which provides built-in functions for MST, or write custom code using standard data structures.
Kruskal’s algorithm builds a Minimum Spanning Tree in Python by sorting all edges and adding the shortest ones while avoiding cycles, often using a Disjoint Set data structure.
Yes, you can visualize a Minimum Spanning Tree in Python using matplotlib with NetworkX to draw the graph and highlight the MST edges for better understanding.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others




Login/Signup to comment