Merge Sort in Python
Sorting – Merge Sort in Python
Merge sort in Python is a comparison-based sorting algorithm that follows the divide-and-conquer strategy to sort an array or list.
You’ll learn how to implement this algorithm, grasp its time and space complexities, and gain insights into when and why Merge Sort is an excellent choice for sorting tasks.
What is Merge Sort in Python?
Merge Sort is a highly efficient and stable sorting algorithm. It operates by dividing an array into smaller equal-sized subarrays, recursively sorting these subarrays, and then merging them back together into a single, sorted array.
Pseudocode for Merge Sort:
MergeSort(arr):
If the length of arr is less than or equal to 1:
Return arr # Base case, nothing to sort
Mid = length of arr // 2 # Find the middle index
Left_half = arr[0:Mid] # Split arr into left and right halves
Right_half = arr[Mid:]
# Recursively sort both halves
Left_half = MergeSort(Left_half)
Right_half = MergeSort(Right_half)
# Merge the sorted halves
Sorted_arr = Merge(Left_half, Right_half)
Return Sorted_arr
Merge(left, right):
Result = an empty list
Left_index = 0
Right_index = 0
# Compare and merge elements from left and right subarrays
While Left_index < length of left and Right_index < length of right:
If left[Left_index] < right[Right_index]:
Append left[Left_index] to Result
Increment Left_index
Else:
Append right[Right_index] to Result
Increment Right_index
# Append remaining elements from left and right (if any)
Append remaining elements from left[Left_index:] to Result
Append remaining elements from right[Right_index:] to Result
Return Result
What is Divide and Conquer Strategy?
Divide and Conquer is a problem-solving strategy in computer science and mathematics. It involves breaking down a complex problem into smaller, more manageable subproblems, solving each subproblem independently, and then combining the solutions of the subproblems to obtain the solution to the original problem.
Working of Merge Sort in Python
The Merge Sort algorithm in Python operates using a divide-and-conquer strategy to sort an array or list efficiently. Here’s a step-by-step explanation of how Merge Sort works:
Divide: The input array is divided into two equal or nearly equal halves. This division continues recursively until each subarray contains only one element or is empty (base case).
Conquer: Starting from the base case, Merge Sort begins merging the subarrays back together in a sorted order. It does this by comparing the elements in the two subarrays and selecting the smaller element to merge first. This process is repeated for all pairs of subarrays.
Combine: The merging process continues upward, merging pairs of sorted subarrays to create larger sorted subarrays. This process continues until the entire array is sorted.
Repeat and Conquer: Merge Sort recursively divides, conquers, and combines subarrays until the entire input array is sorted.
Final Sorted Array: The result is a fully sorted array that preserves the order of elements from the original input.
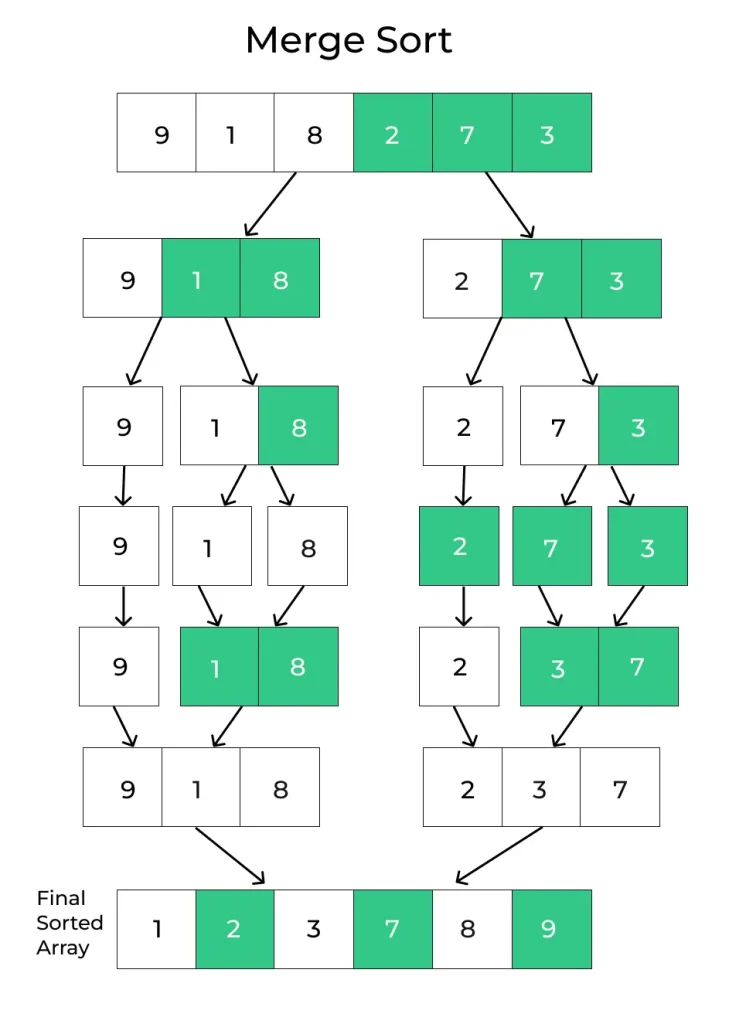
Algorithm for Merge Sort in Python
Algorithm describes the steps for performing Merge Sort:
This algorithm follows these steps:
Divide the input array into two roughly equal halves. This is typically done by finding the midpoint of the array.
Apply the Merge Sort algorithm recursively to both halves of the array. Continue this process until each subarray has only one element (the base case).
Merge the sorted subarrays back together into a single sorted array. This is done by comparing elements from each subarray and arranging them in ascending order.
Continue merging subarrays until you have a single sorted array that encompasses the entire input.
- The result is a fully sorted array containing all the elements from the original input.
Example of Merge Sort in Python using Recursion
def merge_sort(arr):
if len(arr) > 1:
mid = len(arr) // 2
left_half = arr[:mid]
right_half = arr[mid:]
merge_sort(left_half)
merge_sort(right_half)
i = j = k = 0
while i < len(left_half) and j < len(right_half):
if left_half[i] < right_half[j]:
arr[k] = left_half[i]
i += 1
else:
arr[k] = right_half[j]
j += 1
k += 1
while i < len(left_half):
arr[k] = left_half[i]
i += 1
k += 1
while j < len(right_half):
arr[k] = right_half[j]
j += 1
k += 1
my_list = [9, 5, 7, 2, 4, 6]
merge_sort(my_list)
print("Sorted List:", my_list)
Output :
[2, 4, 5, 6, 7, 9]
Explanation
This code demonstrates the Merge Sort algorithm in Python. Merge Sort divides the input list into smaller halves, sorts each half, and then merges them back together. It operates recursively until the entire list is sorted.
- The algorithm’s efficiency and stability make it suitable for various applications.
- In the example, my_list is sorted in ascending order, producing the output “Sorted List” with the sorted result.
Implementation of Merge Sort using 'for' loop
def merge_sort(arr):
if len(arr) <= 1:
return arr
# Split the input list into sublists of size 1
sublists = [[x] for x in arr]
# Merge sublists iteratively until only one remains
while len(sublists) > 1:
merged_sublists = []
for i in range(0, len(sublists), 2):
if i + 1 < len(sublists):
merged = merge(sublists[i], sublists[i + 1])
else:
merged = sublists[i]
merged_sublists.append(merged)
sublists = merged_sublists
return sublists[0]
def merge(left, right):
result = []
left_idx, right_idx = 0, 0
while left_idx < len(left) and right_idx < len(right):
if left[left_idx] < right[right_idx]:
result.append(left[left_idx])
left_idx += 1
else:
result.append(right[right_idx])
right_idx += 1
result.extend(left[left_idx:])
result.extend(right[right_idx:])
return result
# Example usage:
my_list = [3, 6, 8, 10, 1, 2, 1]
sorted_list = merge_sort(my_list)
print(sorted_list)
Output :
[1, 1, 2, 3, 6, 8, 10]
Explanation
In this implementation, the sorting and merging steps are both accomplished using a for loop. When you run this code, it will sort the input list my_list in ascending order, and the sorted list will be displayed as the output.
Implementation of Merge Sort using list
def merge_sort(arr):
if len(arr) <= 1:
return arr
mid = len(arr) // 2
left_half = arr[:mid]
right_half = arr[mid:]
left_half = merge_sort(left_half)
right_half = merge_sort(right_half)
return merge(left_half, right_half)
def merge(left, right):
result = []
left_idx, right_idx = 0, 0
while left_idx < len(left) and right_idx < len(right):
if left[left_idx] < right[right_idx]:
result.append(left[left_idx])
left_idx += 1
else:
result.append(right[right_idx])
right_idx += 1
result.extend(left[left_idx:])
result.extend(right[right_idx:])
return result
# Example usage:
my_list = [3, 6, 8, 10, 1, 2, 1]
sorted_list = merge_sort(my_list)
print(sorted_list)
Output :
[1, 1, 2, 3, 6, 8, 10]
Explanation
In this implementation, Python lists are used for both the merging and sorting steps. When you run this code, it will sort the input list my_list in ascending order, and the sorted list will be displayed as the output.
Time and Space Complexity for Merge Sort
In Python, the Merge Sort algorithm has the following time and space complexities:
Time Complexity (Worst, Average, and Best Case): O(n log n)
- Merge Sort exhibits a consistent time complexity of O(n log n) for worst-case, average-case, and best-case scenarios. This efficiency makes it a reliable choice for sorting, especially for large datasets.
Space Complexity: O(n)
- Merge Sort has a space complexity of O(n) because it requires additional memory for creating temporary arrays during the merging process. This additional memory usage is a notable feature of the algorithm, but it makes Merge Sort a stable and efficient sorting method, even for substantial datasets.
To wrap it up:
Merge Sort’s consistent O(n log n) time complexity, adaptability to various datasets, and stable sorting nature make it a robust choice for sorting tasks. You’ve learned how to implement this algorithm in Python, dissecting its divide-and-conquer strategy and merging technique. With a deep understanding of Merge Sort’s inner workings, you’re now equipped to efficiently sort arrays of any size, making it a valuable addition to your programming toolkit.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Question 1.
What are some variants or optimizations of Merge Sort in Python?
Variants of Merge Sort include “Bottom-Up Merge Sort,” which avoids recursion, and “Natural Merge Sort,” which exploits existing order in the data to improve performance.
Question 2.
How does Merge Sort compare to other sorting algorithms like Quick Sort?
Merge Sort is known for its stability and consistent performance, making it a suitable choice for many scenarios. Quick Sort may perform better in practice but can have worst-case behavior.
Question 3.
Is Merge Sort a stable sorting algorithm?
Yes, Merge Sort is a stable sorting algorithm. It preserves the relative order of equal elements during sorting.
Question 4.
When should I use Merge Sort in Python?
Merge Sort is an excellent choice when stability, predictable performance, and sorting large datasets are essential. It’s often used in applications like external sorting and for sorting data that doesn’t fit entirely in memory.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Login/Signup to comment